1.Понятие вектора. Коллинеарность векторов. Их равенство.

Направленный отрезок или, что то же самое, упорядоченную пару точек будем называть вектором. Обозначается вектор одной буквой  или . Векторы характеризуются длиной  и направлением. Мы рассматриваем свободные векторы, т. е. такие, которые без изменения длины и направления могут быть перенесены в любую точку пространства.

Ортом вектора  называется вектор , который имеет единичную длину и то же направление, что и вектор .

Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными.

Векторы, лежащие в одной плоскости или параллельные одной плоскости, называются компланарными.

Два вектора считаются равными, если они коллинеарные, одинаково направлены и равны по длине.

Пусть даны два вектора. Параллельным переносом приведем их к общему началу. Наименьший угол, на который надо повернуть один вектор до совпадения с другим, называется углом между векторами.

Рис.1

2.Операции над векторами. Их свойства.

Произведением вектора  на действительное число m называется вектор, который удовлетворяет условиям:

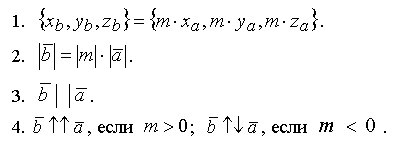
Следовательно, если векторы  и  коллинеарные, то

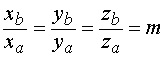
Суммой двух векторов  и  называется вектор , направленный из начала вектора в конец вектора  при условии, что начало совпадет с концом вектора . Если векторы заданы их разложениями по базисным ортам, то при сложении векторов складываются их соответствующие координаты.

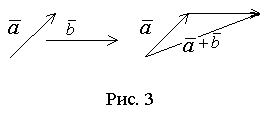Рассмотрим это на примере декартовой системы координат. Пусть

Покажем, что

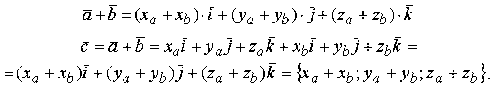
Из рисунка 3 видно, что  

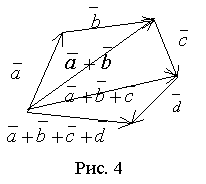
Сумма любого конечного числа векторов может быть найдена по правилу многоугольника (рис. 4): чтобы построить сумму конечного числа векторов, достаточно совместить начало каждого последующего вектора с концом предыдущего и построить вектор, соединяющий начало первого вектора с концом последнего.

Свойства операции сложения векторов:

В этих выражениях m, n - числа.

Разностью векторов  и  называют вектор Второе слагаемое является вектором, противоположным вектору  по направлению, но равным ему по длине.

Таким образом, операция вычитания векторов заменяется на операцию сложения

В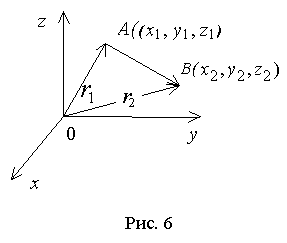ектор , начало которого находится в начале координат, а конец - в точке А (x1, y1, z1), называют радиус-вектором точки А и обозначают  или просто . Так как его координаты совпадают с координатами точки А, то его разложение по ортам имеет вид  

Вектор , имеющий начало в точке А(x1, y1, z1) и конец в точке B(x2, y2, z2), может быть записан в виде

где   - радиус-вектор точки В;  - радиус-вектор точки А.

Поэтому разложение вектора по ортам имеет вид

Его длина равна расстоянию между точками А и В

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними, т.е.

Из определения следует

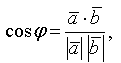
где φ - угол между векторами.

Скалярная величина  называется проекцией вектора  на вектор 

В зависимости от значения угла между векторами, проекция может принимать отрицательные, положительные или нулевое значения.

Теперь можно написать

Из определения скалярного произведения следует, что если векторы ортогональны, то (условие ортогональности ненулевых векторов).