43). Логарифмічний нормальний закон розподілу

Нехай Y має закон розподілу,

- ∞<y<∞.

Необхідно знайти f(x), якщо Х=. Таким чином, Y є функцією випадкового аргументу Х. Тоді Оскільки

Отже,

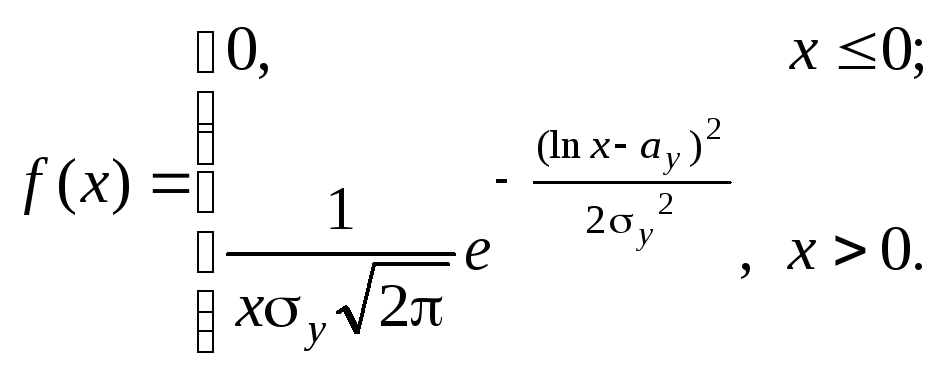
Закон розподілу випадкової величини Х із цією щільністю називають логарифмічним нормальним законом.

41). Показниковий закон розподілу

. .

Щільність розподілу випадкової величини, розподіленої за показниковим законом, задається формулою:

Випадкові величини з таким законом розподілу широко застосовуються в задачах з теорії надійності та теорії масового обслуговування. Числові характеристики:

Ме=ln2/a.

Серед усіх законів неперервних випадкових величин лише експоненціальному притаманна властивість – відсутність післядії, а саме: якщо пов”язати випадкову величину із часом, то для цього закону минуле не впливає на передбачення подій у майбутньому. Цю властивість закону використовують у харківських випадкових процесах, теорії масового обслуговування, теорії надійності.

52) Числові характеристики:

вибіркова середня величина . Величину, яка визначається формулою

називають вибірковою середньою величиною дискретного статистичного розподілу вибірки.

Тут x_i — варіанта варіаційного ряду вибірки;

n_i — частота цієї варіанти;

n — обсяг вибірки ().

Якщо всі варіанти з’являються у вибірці лише по одному разу, тобто n_i = 1, то

2) дисперсія. Для вимірювання розсіювання варіант вибірки відносно вибирається дисперсія.

Дисперсія вибірки — це середнє арифметичне квадратів відхилень варіант відносно , яке обчислюється за формулою

або

3) середнє квадратичне відхилення вибірки _B. При обчисленні D_B відхилення підноситься до квадрата, а отже, змінюється одиниця виміру ознаки Х, тому на основі дисперсії вводиться середнє квадратичне відхилення

яке вимірює розсіювання варіант вибірки відносно , але в тих самих одиницях, в яких вимірюється ознака Х;

50) Кількісні ознаки елементів генеральної сукупності можуть бути одновимірними і багатовимірними, дискретними і неперервними.

Коли реалізується вибірка, кількісна ознака, наприклад Х, набуває конкретних числових значень (Х = х_і), які називають варіантою.

Зростаючий числовий ряд варіант називають варіаційним.

Кожна варіанта вибірки може бути спостереженою n_i раз (n_i  1 ), число n_i називають частотою варіанти x_i.

При цьому

, (350)

де k — кількість варіант, що різняться числовим значенням;

n — обсяг вибірки.

Відношення частоти n_i варіанти x_i до обсягу вибірки n називають її відносною частотою і позначають через W_i , тобто

. (351)

Для кожної вибірки виконується рівність

. (352)

Якщо досліджується ознака генеральної сукупності Х, яка є неперервною, то варіант буде багато. У цьому разі варіаційний ряд — це певна кількість рівних або нерівних частинних інтервалів чи груп варіант зі своїми частотами.

Такі частинні інтервали варіант, які розміщені у зростаючій послідовності, утворюють інтервальний варіаційний ряд.

На практиці для зручності, як правило, розглядають інтервальні варіаційні ряди, у котрих інтервали є рівними між собою.

.38) Гіпергеометричний закон розподілу.

Він описує йм-сть настання m-успішних результатів у випробуваннях, якщо значення n мале порівняно з обсягом сукупності N:

Цей закон застосовується у задачах статистичного контролю та в суміжних галузях. Числові характеристики розподілу:

Зі зменшенням відношення n/N гіпергеометричний розподіл наближається до біноміального з параметрами n i p= k/N. Дуже часто цей розподіл апроксимується розподілом Пуассона, якщо a=nk/N.