36)Формула Пуассона для найпростішого потоку

Імовірність того ,що за проміжок часу t+△t не відбудеться жодна подія ,подається у вигляді

Імовірність того, що за цей самий проміжок часу здійсниться т подій, визначається так

Поділимо ліву і праву частини системи рівнянь на ∆t і вико­наємо граничний перехід при ∆t -0

У результаті дістанемо систе­му лінійних диференціальних рівнянь:

Імовірність того ,що за час t відбудеться m випадкових подій ,які утворюють найпростіший потік ,обчислюється за формулою

P_m(t)= (λt)^m*e^-λt /m! де λ-інтенсивність найпростішого потоку, тобто :середне число подій ,які відбудуться за одиницю часу.

42. Розподіл Фішера. Якщо випадкові величини незалежні і мають — розподіл відповідно з ступенями волі, то випадкова величина має розподіл Фішера з ступенями волі. Щільність цього розподілу подається формулою:

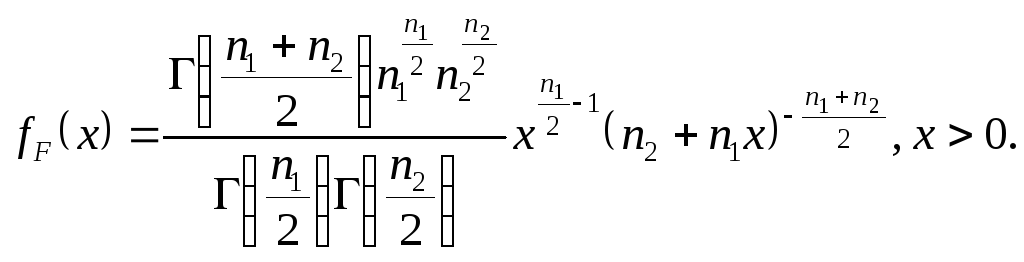Щільність розподілу Фішера має графік, зображений на

Для розподілу Фішера складено таблиці, в яких для відповідної кількості ступенів волі для ймовірностей наведено значення –

. Розподіл Стьюдента. Розподіл Стьюдента з n cтупенями волі має випадкова величина де Х — нормально розподілена величина з нульовим математичним сподіванням і одиничною дисперсією, а . Випадкова величина не залежить від Х і має розподіл з n ступенями волі. Щільність розподілу Графік щільності розподілу Стьюдента за зовнішнім виглядом нагадує нормальні криві. Але вони значно повільніше спадають до осі t, якщо особливо за малих значень n

Складено таблиці розподілу Стьюдента, здебільшого виду для кількості ступенів волі від 1 до 20. Якщо кількість ступенів волі більша, то можна застосовувати нормальний закон розподілу з нульовим математичним сподіванням і одиничною дисперсією.

M(Z)=0. .

54) Визначення статистичної оцінки Інформація, яку дістали на основі обробки вибірки про ознаку генеральної сукупності, завжди міститиме певні похибки, оскільки вибірка становить лише незначну частину від неї (n < N), тобто обсяг вибірки значно менший від обсягу генеральної сукупності.Тому слід організувати вибірку так, щоб ця інформація була найбільш повною (вибірка має бути репрезентативною) і забезпечувала з найбільшим ступенем довіри про параметри генеральної сукупності або закон розподілу її ознаки. Параметри генеральної сукупності M(x_i)=X_г, D_г, δ_г, Mo, r_xy є величинами сталими, але їх числове значення невідоме. Ці параметри оцінюються параметрами вибірки: які дістають при обробці вибірки. Вони є величинами непередбачуваними, тобто випадковими.

Тут через θ позначено оцінювальний параметр генеральної сукупності, а через — його статистичну оцінку, яку називають ще статистикою. При цьому θ = const, а — випадкова величина, що має певний закон розподілу ймовірностей. Зауважимо, що до реалізації вибірки кожну її варіанту розглядають як випадкову величину, що має закон розподілу ймовірностей ознаки гене­ральної сукупності з відповідними числовими характеристиками:M(x_i)=X_г=M(x), D(x_i)=D_г, δ(x_i)=δ_г