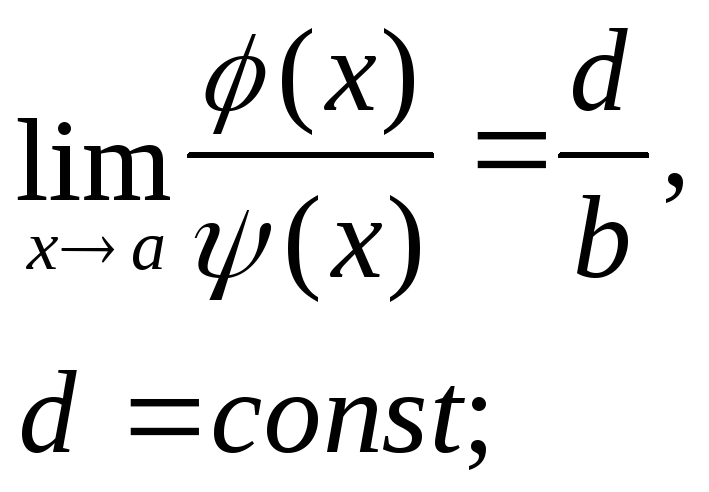- •Содержание
- •Глава 1.
- •Глава 2.
- •Глава 3.
- •Глава 4.
- •Глава 5.
- •Глава 6.
- •Глава 7.
- •Глава 8.
- •Введение
- •Глава 1. Матрицы, определители, системы линейных уравнений
- •1.1. Матрицы и действия над ними
- •1.2. Определители и их вычисление
- •1.3. Ранг матрицы
- •Метод окаймляющих миноров нахождения ранга матрицы
- •Алгоритм приведения матрицы к ступенчатому виду элементарными преобразованиями
- •Свойства матриц и определителей
- •1.4. Обратная матрица
- •1.5. Исследование и решение произвольной системы линейных алгебраических уравнений
- •Глава 2. Векторная алгебра и аналитическая геометрия
- •2.1. Элементы векторной алгебры
- •П Точка , точка роизведения векторов элементы векторной алгебры
- •2.2. Геометрия прямых и плоскостей в таблицах
- •Уравнения плоскости р в трехмерном пространстве r3 и уравнения прямой l в двухмерном пространстве r2
- •Уравнения прямой l в трехмерном пространстве r3 и в двухмерном пространстве r2
- •Взаимное расположение плоскостей p в трёхмерном пространстве r3 и прямых l в двухмерном пространстве r2
- •Расстояния d(p1,p2) между плоскостями p1 и p2 и d(l1,l2) между прямыми l1 и l2 в r3, пересечение pl плоскости p и прямой l в r3
- •Полярная система координат
- •Поверхности второго порядка
- •Глава 3. Предел и непрерывность функции одного аргумента
- •3.1. Вычисление пределов
- •Предел дробно-рациональной функции
- •Сравнение бесконечно малых функций
- •Предел отношения б. М. Ф. (б. Б. Ф.) не изменится, если заменить эти функции эквивалентными.
- •Разность эквивалентных б. М. Ф. (б. Б. Ф.) есть б. М. Ф. (б. Б. Ф.) более высокого порядка малости (роста) по сравнению с уменьшаемой и вычитаемой б. М. Ф. (б. Б. Ф.).
- •Сумма конечного числа б. М. (б. Б.) слагаемых разного порядка малости (роста) эквивалентна слагаемому самого низкого (высокого) порядка малости (роста).
- •3.2. Непрерывность функции одного аргумента
- •Глава 4.
- •4.1. Таблица производных
- •Правила дифференцирования
- •Сложная функция
- •Параметрически заданная функция
- •8. Логарифмическое дифференцирование
- •4.2. Таблица интегралов
- •4.3. Приложения производной Теоремы Роля, Лагранжа, Коши
- •Раскрытие неопределенностей по правилу Лопиталя
- •Исследования функции без применения производных
- •Исследования функции с применением производных
- •4.4. Неопределенный интеграл Метод непосредственного интегрирования
- •Метод интегрирования по частям
- •План интегрирования рациональных дробей
- •Интегрирование тригонометрических и гиперболических функций
- •Интегрирование иррациональностей
- •4.5. Несобственные интегралы (н.И.)
- •4.6. Приложения определенного интеграла
Полярная система координат
Полярная система координат состоит из некоторой точки О, называемой полюсом, и исходящего из нее луча ОЕ, называемого полярной осью. Кроме этого задается единица масштаба для измерения длин отрезков.
![]() это
расстояние от точки М
до полюса О,
это
расстояние от точки М
до полюса О,
![]() угол,
на который нужно повернуть против
часовой стрелки полярную ось для
совмещения с лучом ОМ.
угол,
на который нужно повернуть против
часовой стрелки полярную ось для
совмещения с лучом ОМ.
Полярные и декартовы координаты точки связаны соотношениями:
![]() .
.
Чтобы
получить изображение кривой в полярной
системе координат, постройте лучи,
выходящие из полюса 0 под углами j
к полярной оси. На каждом луче отложите
длину вычисленного Вами полярного
радиуса r.
Если r –
отрицательное число, то для построения
соответствующей точки нужно отложить
модуль r
на луче, повёрнутом на 180°
вокруг полярной оси, то есть отложить
от полярной оси угол
![]() .
Соедините построенные Вами точки плавной
линией.
.
Соедините построенные Вами точки плавной
линией.
Кривые,
уравнения которых в полярной системе
координат имеют вид
![]() ,
,
![]() ,
называют розами. Причем, если
,
называют розами. Причем, если
![]() – чётное, то лепестков
– чётное, то лепестков
у
розы
![]() ,
а если число
,
а если число
![]() – нечётное, то у розы
– нечётное, то у розы
![]() лепестков.
лепестков.
Поверхности второго порядка
|
№ |
Вид поверхности второго порядка |
Уравнение |
Рисунок |
|
1 |
Эллипсоид |
|
|
|
2 |
Мнимый эллипсоид |
|
|
|
3 |
Однополостный гиперболоид |
|
|
|
4 |
Двуполостный гиперболоид |
|
|
|
5 |
Эллиптический параболоид |
|
|
|
6 |
Гиперболический параболоид |
|
|
|
7 |
Конус |
|
|
|
8 |
Мнимый конус |
|
|
|
9 |
Эллиптический цилиндр |
|
|
|
10 |
Гиперболический цилиндр |
|
|
|
11 |
Параболический цилиндр |
Y 2 = 2pX |
|
|
12 |
Мнимый эллиптический цилиндр |
|
|
|
13 |
Пара мнимых пересекающихся плоскостей |
|
|
|
14 |
Пара пересекающихся плоскостей |
|
|
|
15 |
Пара параллельных плоскостей |
X 2 − a2 = 0 |
|
|
16 |
Пара мнимых параллельных плоскостей |
X 2 + a2 = 0 |
|
|
17 |
Пара совпавших плоскостей |
X 2 = 0 |
|
Глава 3. Предел и непрерывность функции одного аргумента
3.1. Вычисление пределов
|
Определение понятия функции одного аргумента |
Если
каждому элементу х
из множества Х
( Элементы
Множество Х называется областью определения функции, а множество всех значений функции – областью значений функции. В случаях, когда множества Х и Y числовые множества, соответствующие функции, называют числовыми функциями. |
|
Основные элементарные функции |
Степенная
Показательная
Логарифмическая
Тригонометрические
Обратные тригонометрические
постоянная
|
|
Определение элементарных функций |
Элементарными называют функции, которые получаются из основных элементарных функций в результате применения к ним конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции (суперпозиции) функций. |
|
Определение предела функции f(x) в точке x = a.
|
Число
A
называется пределом функции f(x)
при х,
стремящемся
к a
( Используя логические символы, можно записать:
|
Геометрический смысл этого определения заключается в следующем.
Какую
бы узенькую полоску шириной 2![]() ,
параллельную оси абсцисс и содержащую
прямую y
= A
посередине (
,
параллельную оси абсцисс и содержащую
прямую y
= A
посередине (![]()
окрестность точки y = A:
окрестность точки y = A:
![]() ),
мы ни выделили, всегда существует такой
симметричный интервал длиной 2
),
мы ни выделили, всегда существует такой
симметричный интервал длиной 2![]() с центром в точке х
= а,
с центром в точке х
= а,
![]() (проколотая
(проколотая
![]()
окрестность точки х
= а:
окрестность точки х
= а:
![]() ),
что для всех х
из проколотой
),
что для всех х
из проколотой
![]()
окрестности точки х =
а
значения функции f
(x)
попадают в
окрестности точки х =
а
значения функции f
(x)
попадают в
![]()
окрестность точки y
= A:
окрестность точки y
= A:


Для любого ипсилон больше нуля положительное дельта найдется,
Такое, что если х из проколотой дельта – окрестности точки а любой берется,
Значение функции f(х) в ипсилон – окрестность точки А попадется.
|
Определение
предела функции при
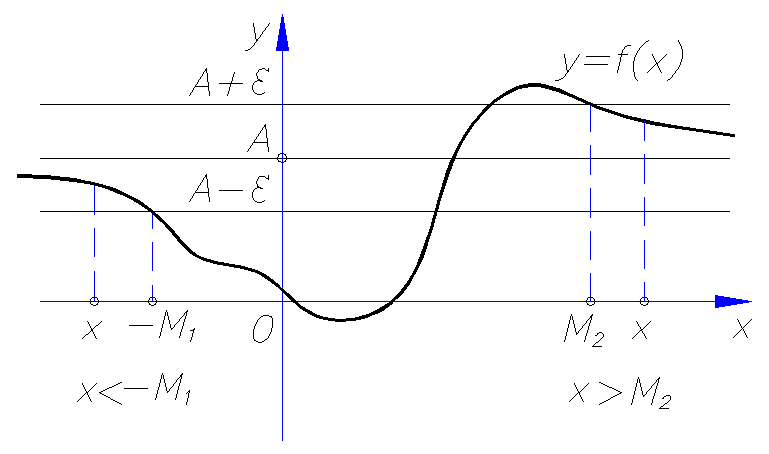
|
Число
А называется
пределом функции y
= f(x)
при стремлении х
к бесконечности, если для любого
положительного сколь угодно малого
числа
|
В
частности, если
![]() ,
то
,
то
![]()
если
же
![]() ,
тогда
,
тогда
![]()
Неравенство
![]()
эквивалентно системе двух неравенств:
эквивалентно системе двух неравенств:
![]() .
.
|
Определение непрерывной в точке х = x0 функции |
Функция f(x) называется непрерывной в точке х0
|
1.6.
|
Три условия для непрерывной в точке x = х0 функции |
в этой точке. |
1.7.
|
Теорема о непрерывности элементарных функций |
Все элементарные функции непрерывны во всех точках области определения этих функций. Для элементарных функций предел функции в точке равен значению этой функции в данной точке. |
Раскрытие
неопределённости вида
![]()
|
|
c = const ≠ 0, b = const ≠ 0 |
||
|
№ n/n |
Вид функции f(x) |
Какие преобразования нужно сделать |
Результат преобразований |
|
1 |
|
Разделить многочлены Pn(x) и Qm(x) на разность (х а), сократить f(x) на эту разность (х а) и подставить вместо х значение х = а. |
приём |
|
2 |
Функция f(x) содержит иррациональность вида
|
Умножить и разделить функцию f(x) на сопряженное иррациональное выражение
использовать формулу сокращенного умножения (А–В)(А+В)=А2–В2 и сократить f(x) на разность (х – а).
|
------ // ------ |
|
3 |
Функция f(x) содержит иррациональность вида
или
|
Умножить и разделить разность кубических корней на неполный квадрат суммы, а сумму кубических корней – на неполный квадрат разности, воспользоваться формулами сокращенного умножения: (А–В)(А2+АВ+В2)=А3–В3; (А+В)(А2– АВ+В2)=А3+В3 и сократить функцию f(x) на разность (х – а). |
приём |
Замечание.
При делении многочлена Pn(x) или Qm(x) на разность (х – а) опираются на теорему Безу: если число х = а является корнем многочлена (при х = а многочлен равен нулю), то этот многочлен делится на разность (х – а) без остатка.
Деление многочлена на разность (х – а) осуществляется по тем же правилам, по которым делятся столбиком числа:
 _a0xn
+
a1xn-1
+ a2xn-2
+ … + an
x
a
_a0xn
+
a1xn-1
+ a2xn-2
+ … + an
x
a
 a0xn
aa0xn-1
a0xn-1
+ (a1
+ aa0)xn-2
+ … = Pn-1(x)
a0xn
aa0xn-1
a0xn-1
+ (a1
+ aa0)xn-2
+ … = Pn-1(x)
_ (а1 + aa0)xn-1 + a2xn-2
(a1 + aa0)xn-1 – a(a1 + aa0)xn-2
_ (a2 + a(a1 + aa0))xn-2 + a3xn-3
……………………………
……………………………
0
Обратите внимание на то, что индекс в обозначении многочлена соответствует старшей степени х этого многочлена.
В результате деления получим представление многочлена Рn (х) в виде произведения многочлена
Pn-1 (x) на разность (x–a) :
Рn(x) = (x – а) Рn-1(х).