Задание 9.
Прямой код — способ представления двоичных чисел с фиксированной запятой в компьютерной арифметике. При записи числа в прямом коде старший разряд является знаковым разрядом. Если его значение равно 0 — то число положительное, если 1 — то отрицательное.
Обратный код — метод вычислительной математики, позволяющий вычесть одно число из другого, используя только операцию сложения над натуральными числами. При записи числа для положительного числа совпадает с прямым кодом, а для отрицательного числа все цифры заменяются на противоположные, кроме разрядного.
Дополнительный код (англ. two’s complement, иногда twos-complement) — наиболее распространённый способ представления отрицательных целых чисел в компьютерах. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел, чем упрощает архитектуру ЭВМ. При записи числа для положительного числа совпадает с прямым кодом, а для отрицательного числа дополнительный код обуславливается получением обратного кода и добавлением 1.
Сложение чисел в дополнительном коде возникающая 1 переноса в знаковом разряде отбрасывается, а в обратном коде прибавляется к младшему разряду суммы кодов.
Если результат арифметических действий является кодом отрицательного числа необходимо преобразовать в прямой код. Обратный код преобразовать в прямой заменой цифр во всех разрядах кроме знакового на противоположных. Дополнительный код преобразовывается в прямой прибавлением 1.
A
)X
=10111
Y= -11110
Прямой код:
X=0,0010111 1,0011110
Y=1,0011110 0,0010111
1,0000111
Обратный код:
X=0,0010111 0,0010111
Y=1,1100001 1,1100001
1,1111000
1,0000111
Дополнительный код:
X=0,0010111 0,0010111
Y=1,1100010 1,1100010
1,
1111001 1,0000110
1
1,0000111
Б)X=110110
Y=101110
Прямой код:
X=0,110110
Y=0,101110
Обратный код:
X=0,110110 0,0110110
Y=0,101110 0,0101110
0,1100100
Дополнительный код:
X=0,110110 0,0110110
Y=0,101110 0,0101110
0,1100100
Задание 10.
Логические элементы
1. Логический элемент НЕ выполняет логическое отрицание. Он имеет один вход и один выход. Отсутствие сигнала (напряжения) обозначим через «0», а наличие сигнала через «1». Сигнал на выходе всегда противоположен входному сигналу. Это видно из таблицы истинности, которая показывает зависимость выходного сигнала от входного.
У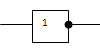
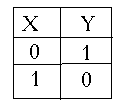словное
обозначение Таблица
истинности
X Y
2. Логический элемент ИЛИ выполняет логическое сложение. Он имеет несколько входов и один выход. Сигнал на выходе будет, если есть сигнал хотя бы на одном входе.
У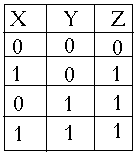
словное
обозначение Таблица истинности
X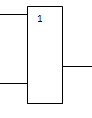
Z
Y
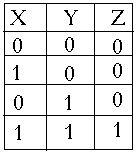
3. Логический элемент И выполняет логическое умножение. Сигнал на выходе этого логического элемента будет только в том случае, если есть сигнал на всех входах.
Условное обозначение Таблица истинности
X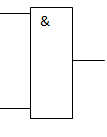
Z
Y
F
=(¬A
v
¬B
) ʌ (¬C
v
¬D)
Таблица 10.1 – Таблица истинности
|
A |
B |
C |
D |
¬A |
¬B |
¬C |
¬D |
(¬A v ¬B ) |
(¬C v¬D) |
F=(¬A v ¬B ) ʌ (¬C v ¬D) |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1
A 1
1 &
B
1 1
F
C
1
D
