Задача 7

Бригада рабочих за смену изготавливает n деталей. Вероятность того, что каждая изготовленная деталь высшего качества равна p. Какова вероятность того, что за смену изготовлено m деталей высшего качества?

Дано:

	n	p	m
14	800	0.4	600

Решение:

Условие задачи соответствует схеме независимых испытаний. Испытание – изготовление детали. Число испытаний n = 800. Каждое испытание имеет два взаимоисключающих исхода: изготовленная деталь высшего качества (вероятность этого исхода p = 0.4); изготовленная деталь не высшего качества (вероятность этого исхода q = 1 – p = 1 – 0.4 = 0.6).

Так как число испытаний велико, то применим локальную теорему Муавра-Лапласа:

, где , , функция .

Значение функции находим из таблицы.

Событие A – из 800 изготовленных за смену деталей 600 высшего качества. Вероятность события A – это .

; , , .

.

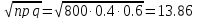Ответ: вероятность того, что из 800 изготовленных за смену деталей 600 окажется высшего качества, равна 0.

Задача 8

Вычислительное устройство состоит из n независимо работающих элементов. Вероятность выхода из строя каждого элемента одинакова и равна p. Составить закон распределения случайной величины ξ – числа отказавших элементов. Построить график функции распределения F(x). Найти M(ξ) и D(ξ).

Дано:

	n	p
14	3	0.1

Решение:

Условие задачи соответствует схеме независимых испытаний Бернулли. Испытание – работа элемента. Каждое испытание имеет два взаимоисключающих исхода: событие A – элемент вышел из строя (вероятность p(A) = p = 0.1), событие – элемент не вышел из строя (вероятность p( Вероятность наступления события A k раз в n независимых испытаний вычисляется по формуле Бернулли:

.

Составим закон распределения случайной величины ξ – числа отказавших элементов:

ξ = 0;

ξ = 1;

ξ = 2;

ξ = 3;

Проверка:

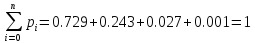, следовательно закон распределения составлен верно.

Определим числовые характеристики распределения Mξ и Dξ:

;

.

;

.

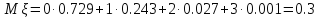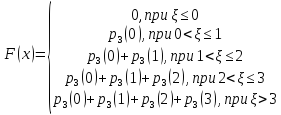
В числовом виде:

Задача 9

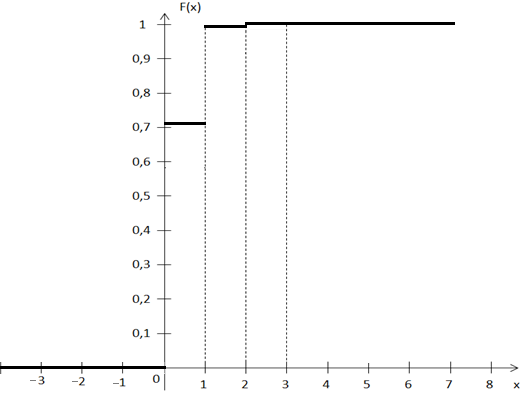
Задана плотность распределения вероятностей f(x). Определить коэффициент a, функцию распределения F(x), M(, D(, вероятность попадания случайной величины в интервал . Построить графики функций F(x) и f(x).

Дано:

α = 0, β = 1/2,

Решение:

1. Найдем коэффициент a из условия

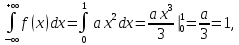
откуда a=3.

2. Определим

При , тогда

При , , тогда

При , тогда .

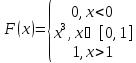
3. Построим графики функций f(x) и F(x):

4. Определим M() и D():

5. Определим

Задача 10

Завод выпускает детали, стандартная длина которых a мм. Рассмотрим длину детали как случайную величину ξ, распределенную по нормальному закону со средним квадратическим отклонением ϭ и математическим ожиданием a, определить: 1) вероятность того, что длина наудачу выбранной детали будет больше α и меньше β; 2) вероятность отклонения длины детали от стандартного размера a больше чем на δ мм.

Дано:

	a	ϭ	α	β	δ
14	28	9	20	32	3

Решение:

Для нормально распределенной случайной величины с параметрами а, σ вероятность попадания случайной величины в интервал (α;β) определяется выражением:

, где - интегральная функция Лапласа.

Функция Ф(z) – нечетная. Значение функции Ф(z) выбирается из таблицы.

Вероятность отклонения случайной величины от ее математического ожидания а более чем на δ определяется выражением:

1) Подставляя в выражение (1) соответствующие значения, определим вероятность того, что длина наудачу выбранной детали будет больше 20 и меньше 32 мм:

2) Подставляя в выражение (2) соответствующие значения, определим вероятность отклонения длины ξ наудачу выбранной детали от стандартного размера 28 мм более чем на 3 мм:

Ответ: вероятность того, что длина наудачу выбранной детали будет больше 20 мм и меньше 32 мм равна 0,4833, а вероятность отклонения детали от стандартного размера 28 мм более чем на 3 мм равна 0,7414.