Федеральное государственное образовательное учреждение
высшего профессионального образования
«Сибирский федеральный университет»
|
Космических и информационных технологий |
|
институт |
|
Прикладной математики и компьютерной безопасности |
|
кафедра |
Типовой расчет Тема: «Теория вероятностей» Вариант 14
|
Теория вероятностей и математическая статистика |
|
дисциплина |
|
Преподаватель |
|
|
|
Шлепкин А. К. |
|
|
|
подпись, дата |
|
фамилия, инициалы |
|
Студент |
КИ10-07 |
|
|
|
Пендик И. О. |
|
|
код (номер) группы |
|
подпись, дата |
|
фамилия, инициалы |
Красноярск, 2011
Задача 1
В ящике 20 шаров с номерами 1,2,…,20. Наудачу выбирают 6 шаров. Найти вероятность того, что среди них есть шары с номерами 1 и 2.
Решение:
Число возможных способов выбрать 6 шаров из 20:

Событие A: среди 6-ти выбранных шаров есть шары с номерами 1 и 2.
Число способов выбрать 6 шаров из 20, благоприятствующее наступлению события A:

По определению вероятности:

Ответ: вероятность того, что среди 6-ти шаров, выбранных из 20-ти, есть шары с номерами 1 и 2 равна 0.079
Задача №2
Определить вероятность безотказной работы за время Т работы электрической цепи, состоящей из пяти независимо работающих элементов. Вероятности отказов элементов за время Т заданы таблицей.
Дано:
|
e |
e1 |
e2 |
e3 |
e4 |
e5 |
|
p |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |

Решение.
Событие А – безотказная работа всей цепи за время Т.
Событие
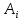 – безотказная работа i-го
элемента цепи за время Т.
– безотказная работа i-го
элемента цепи за время Т.
Событие
 – отказ i-го элемента цепи
за время Т.
– отказ i-го элемента цепи
за время Т.
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
Тогда
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Согласно схеме цепи:
 .
.
Поскольку элементы цепи независимы друг от друга, то




Задача 3
Игра
между A и B
ведется на следующих условиях: первый
ход всегда делает A, он
может выиграть с вероятностью
 ,
если A не выигрывает, то
ход делает B и может
выиграть с вероятностью
,
если A не выигрывает, то
ход делает B и может
выиграть с вероятностью
 .
Если B не выигрывает, то
A делает второй ход, который
может привести к выигрышу с вероятностью
.
Если B не выигрывает, то
A делает второй ход, который
может привести к выигрышу с вероятностью
 .
Если A вторым ходом
проигрывает, то победителем считается
B. Найти вероятность
выигрыша для A и B.
.
Если A вторым ходом
проигрывает, то победителем считается
B. Найти вероятность
выигрыша для A и B.
Дано:
|
|
|
|
|
|
14 |
0.6 |
0.5 |
0.2 |
Решение:
Пусть:
Событие
 – игрок A выиграл с первого
раза;
– игрок A выиграл с первого
раза;
Событие
 – игрок A не выиграл с
первого раза;
– игрок A не выиграл с
первого раза;
Событие
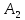 – игрок A выиграл со
второго раза;
– игрок A выиграл со
второго раза;
Событие
 – игрок A не выиграл со
второго раза;
– игрок A не выиграл со
второго раза;
Событие
 – игрок B выиграл с первого
раза;
– игрок B выиграл с первого
раза;
Событие
 - игрок B не выиграл с
первого раза;
- игрок B не выиграл с
первого раза;
Событие
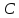 – выиграл игрок A;
– выиграл игрок A;
Событие
 -
выиграл игрок B.
-
выиграл игрок B.
Выразим
события C и D
через события
 ,
,
 ,
,
 ,
,
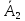 ,
,
 ,
,
 :
:
 ;
;
 .
.

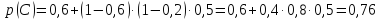


Ответ: вероятность выигрыша для игрока А равна 0,76; вероятность выигрыша для игрока В равна 0,24.