27. Какова связь между истинной и средней теплоемкостями? Как вычисляется тепло в процессе через истинную и среднюю тепло­емкости? (5)

Теплоемкость в данной точке, т.е. на бесконечно малом участке рассматриваемого термодинамического процесса х = const изменения состояния системы называется истинной. Она обозначается с соблюдением всех вышеизложенных правил с помощью буквы «с».

В практике приходится иметь дело с конечными процессами, когда изменение температуры ТС изменяется от значения t₁ до значения t₂. В этом случае удобно использовать понятие средней теплоемкости вещества в процессе х = const в интервале температур t₁—t₂. Указанная теплоемкость обозначается следующим образом: . С ее помощью удельная теплота процесса на участке с начальной температурой t₁ и конечной температурой t₂ определяется:

,

где - средняя удельная теплоемкость ТС в рассматриваемом процессе х=const на участке с начальной температурой t₁ и конечной температурой t₂.

Из данного соотношения очевидно определение средней теплоемкости ТС в том или ином процессе х = const. в интервале температур t₁—t₂

Взаимосвязь средней и истинной теплоемкости:

= ; = .

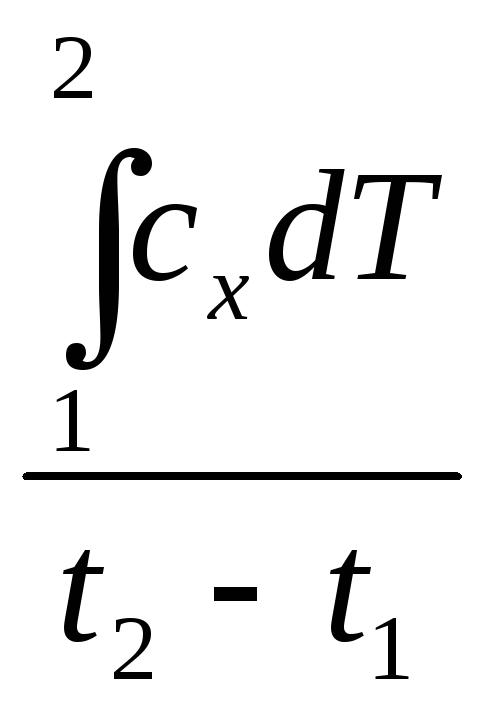С помощью истинной теплоемкости теплота процесса 1-2 определяется:

q=,

где - истинной теплоемкости теплота процесса 1-2.

Из данного соотношения очевидно определение истинной теплоемкости:

=.

Контрольная работа 2 (первая часть курса Задачи

1. 4 кг воздуха расширяются изотермически при температуре t=50° С так, что его объем возрастает в 3,5 раза, а давление стано­вится равным p=0,1 МПа. Определить начальный я и конечный объе­мы газа, количество подводимого к нему тепла и изменение его энт­ропии.

Дано: Найти:

m(возд)=4 кг; V₁=?;

t=50˚C; V₂=?;

V₂=3.5V₁; q₁=?;

p₂=0.1 МПа; ∆S=?;

T=const;

P1=0.1 МПа t1=50˚C V1

p2=0.1 МПа t2=50˚C V2

Рис.1

Решние:

Т.к. изотермическое расширение воздуха ,то используем закон Бойля-Мариотта:

pV=const ,при T=const p₁V₁= p₂V₂ (2) .Учитывая ,что V₂=3.5V₁,получаем:

p₁V₁= p₂V₁*3.5 p₁= 3.5p₂; p₁=0.35 МПа;

Воспользуемся уравнением Менделеева-Клапейрона: pV=mRT/M. (1)

Для начального состояния воздуха:

p₁V₁=mRT₁/M,где p₁- давление воздуха в начальном состоянии; m- масса воздуха ; T-температура воздуха. Найдем объем воздуха в начальном состоянии:

V₁= mRT/ p₁M =4*8314*323/0.35*10⁶*28.9=1.06 (м³).

Для конечного состояния воздуха:

p₁V₁=mRT₁/M,где p₁- давление воздуха в конечном состоянии; m- масса воздуха ; T-температура воздуха. Найдем объем воздуха в конечном состоянии:

V₂= mRT/ p₂M =4*8314*323/0.1*10⁶*28.9=3.71 (м³).

Изменение энтропии вычисляем по формуле:

∆S=R*ln(p₂/ p₁)/M=8314*ln(0.35/0.1)/28.9=360.4 (Дж); (1)

Считаем количество подведенного тепла:

q₁=∆S*T=360.4*323=116409 (Дж). (1)

Ответ: V₁=1.06 (м³); V₂=3.71 (м³); ∆S=360.4 (Дж); q₁=116409 (Дж).

16. В процессе политропного сжатия кислорода затрачивается работа L=400 кДж, причем в одном случае от кислорода отводится 600 кДж, а в другом—кислороду сообщается 100 кДж тепла. Оп­ределить показатели обеих политроп. Процессы изобразить в pv- н Ts-диаграммах.

Дано: Найти:

L=-400 кДж; n_a =?;

a) Q₁=100 кДж; n_в =?;

b) Q₂=-600 кДж;

Газ-кислород О₂;

О2

О2

Рис.1

(2)

Для случая (а)-области I-III и VIII;для случая (b)-области IV-VII.

Характеристика молекулы идеального газа	Показатель адиабаты, k	Теплоемкость газов, кДж/(кмольК)
		сv,	сp,
Одноатомная	1,67	12,56	20,93
Двухатомная	1,4	20,93	29,31
Многоатомная	1,33	29,31	37,68

(4)

Решение:

Кислород- двухатомный газ ,следовательно для него принимаем показатель адиабаты k=1.4.

Удельная молярная теплоемкость:c_v,M=20.93 кДж/(кмольК) (см.табл.выше).

Удельная массовая теплоемкость:c_v= c_v,M/M (1);c_v =20.8/32=0.65 кДж/(кгК).

Газовая постоянная для кислорода: R_O2=R/M_O2=0.26 кДж/(кгК) (1) ;

a) Подводимое тепло:

Q₁=c_v(T₂-T₁)(n_a-k)/(n_a-1); (2)

где Q₁-подводимое тепло; T₂ и T₁-конечная и начальная температуры;

n_a-показатель политропы для случая а)

Выражение для затраченной работы:

L=R_O2(T₁-T₂)n_a/( n_a-1); (2)

где L-затрачиваемая работа;

Q₁/L= [c_v(T₁-T₂)(k-n_a)/(n_a-1)]/ [R_O2(T₁-T₂)n_a/( n_a-1)];

Q₁/L= c_v(k-n_a)/n_aR_O2

n_a= c_vkL/(Lc_v+Q₁ R_O2)=0.65*1.4*{-400}/({-400}*0.65+100*0.26)=1.5.

b) Отводимое тепло:

Q₂=c_v(T₂-T₁)(n_b-k)/(n_b-1);

где Q₂-отводимое тепло; T₂ и T₁-конечная и начальная температуры;

n_b-показатель политропы для случая b);

Выражение для затраченной работы:

L=R_O2(T₁-T₂)n_b/( n_b-1);

где L- затрачиваемая работа;

Q₂/L= [c_v(T₁-T₂)(k-n_b)/(n_b-1)]/ [R_O2(T₁-T₂)n_b/( n_b-1)];

Q₂/L= c_v(k-n_b)/n_bR_O2

n_b= c_vkL/(Lc_v+Q₂ R_O2)=0.65*1.4*{-400}/({-400}*0.65+600*0.26)=0.8.

Ответ: n_a=1.5; n_b=0.8.

27. Используя дифференциальное уравнение вывести зависимость энтальпии от температуры и удельного объема для реального газа, подчиняющегося уравнению состояния

Ван-дер-Ваальса 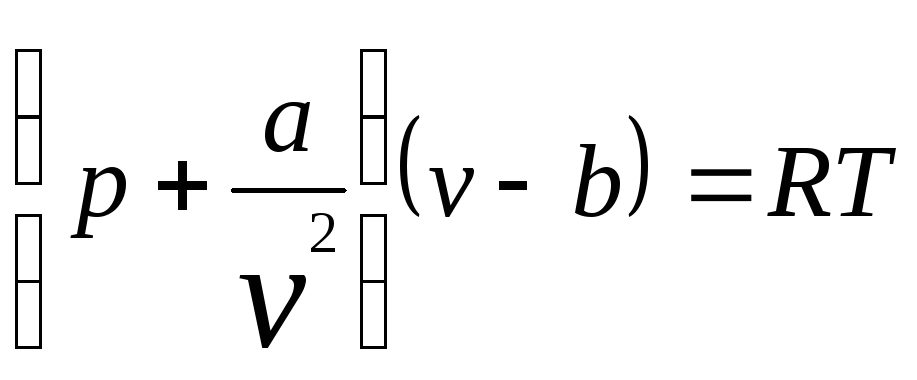Определить для 1 кг водяного пара энтальпию при t=200° С и

v =0,2 м³/кг, если a=1700 Нм⁴/кг², b=0.169 10 ^-2 м³/кг (теплоемкость c_v для Н₂0 взять при заданной температуре из табл. 5 приложения).

Дано: Найти:

m= 1 кг; i=?

t=200° С;

v =0,2 м³/кг;

a=1700 Нм⁴/кг²;

b=0.169 10 ^-2 м³/кг;

Решение:

Находим значение производной из уравнения Ван-дер-Ваальса :

=.

В выражение подставляем значение производной :

=-. Заменив на , получаем:

=.

Проинтегрировав полученное выражение, получаем:

, где ­производная функция от температуры.

Если V, то реальный газ по свойствам стремиться к идеальному, но для него . Поэтому и .

Учитывая, что , а , находим

.

Подставляем значения из условия задачи:

898.6 (кДж/кг).

Ответ: i= 898.6 (кДж/кг).