1. Определение линейного пространства.

Множество V называется линейным пространством, а его элементы 0 веторами, если на нем определены 2 операции:

• Сложение векторов, означающее, что каждым двум векторам по некоторому правилу ставится в соответствие третий вектор, называемый суммой векторов 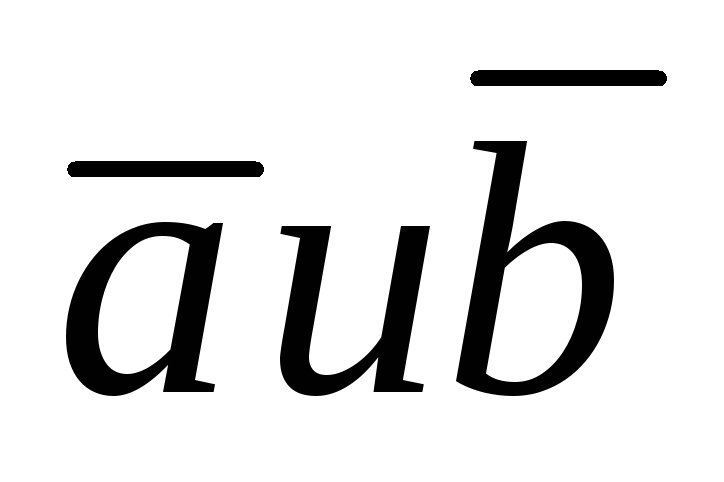и обозначается

• Умножение вектора на число, означающее, что каждой паре, состоящей из вектора и числа λ, ставится в соответствие вектор, называемый произведением λ на и обозначаемый λ.

Указанные операции должны удовлетворять следующим условиям (аксиомам):

1) = +

2) () + = + (+)

3) существует нулевой элемент , такой, что

+= для любого

4) для каждого элемента существует противоположный элемент -, такой, что

+(-) =

5) λ() = λ+ λ

6) (λ+μ) = λ+ μ

7) λ (μ) = (λμ)

8) 1 * =

Где , и - произвольные элементы V, а λ и μ – произвольные действительные числа, которые принято называть скалярами.

2. Дайте определение подпространства линейного пространства.

Пусть V-линейное пространство, а L-произвольное подмножество (LV). Подмножество L называется подпространством линейного пространства V, если оно само является линейным пространством относительно тех же операций сложения и умножения на число, что определены в

Критерии подпространств:

1. для любых двух векторов 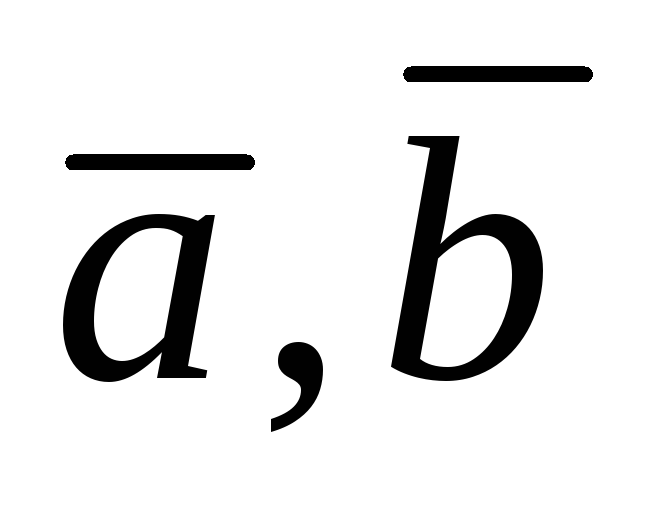из L их сумма также принадлежит L

2. для любого вектора из L и любого действительного числа λ произведение λтакже принадлежит L

Примеры:

1. Множество всех многочленов, заданных на отрезке [a;b]-подпространством линейного пространства функций, заданных на этом отрезке.

2. Множество всех многочленов, степень которых не превышает n-1, является подпространством множества многочленов, степень которых не превышает n.

3. Множество решений однородной системы линейных уравнений с n неизвестными является подпространством пространства R.

dim V≥dim L, где V-линейное пространство, L-его подпростр-во.

Свойства подпространств:

• Подпространство линейного пространства есть линейное пространство

• Размерность подпространства не больше размерности линейного пространства.

• Если e₁, e₂, e₃ – базис подпространства линейного пространства, то

• e_k+1, e_k+2, e_n  R так что, e₁, e₂ e_k  e_n – базис в R.

3. Понятие линейной зависимости и линейной независимости системы векторов, свойства линейной зависимости.

Система векторов а₁,а₂,…,а_s линейного пространства V называется линейно зависимой, если существуют такие числа с₁,с₂,…,с_s , не равные одновременно нулю, что справедливо равенство с₁а₁ + с₂а₂ + … + с_sa_s = 0

Например, ₁ = (2;2;3), ₂ = (0;-4;5), ₃ = (3;13;-8) линейно зависимая система векторов, поскольку =(0;0;0)

Свойства линейной зависимости:

1. Система из одного вектора линейно зависима тогда и только тогда, когда =

2. Система, содержащая более одного вектора, линейно зависима в том и только в том случае, когда среди данных векторов имеется такой, который линейно выражается через остальные.

3. Если часть система зависима , то и вся система зависима.

4. Если система а₁,а₂,…,а_s линейно независима, но при добавлении к ней еще одного вектора становится зависимой, то вектор линейно выражается через а₁,а₂,…,а_{s .}

Если система векторов а₁,а₂,…,а_s такова, что равенство с₁а₁ + с₂а₂ + … + с_sa_s = 0 возможно, только если с₁=с₂= … =с_s = 0, то эта система называется линейно независимой.