Переменный ток

6.1. Переменный электрический ток. Генератор переменного тока

Рис. 6.1. Вращающаяся рамка в магнитном поле

Переменный ток - это ток, периодически меняющийся по величине и направлению. Рассмотрим принцип действия генератора переменного тока на примере вращения рамки из проводника в однородном магнитном поле (рис. 6.1).

Пусть рамка имеет площадь S и первоначально расположена в однородном магнитном поле так, что нормаль к плоскости рамки составляет угол =0 с направлением вектора индукции .

При вращении рамки с угловой скоростью  угол  изменяется по закону, a магнитный поток Ф, пронизывающий рамку,  по закону: . Так как , где Т - период, то .

Изменения магнитного потока возбуждают в рамке ЭДС индук­ции, согласно закону электромагнитной индукции, равную производной от потока по времени (строчными буквами мы будем обозначать мгновенные значения):

.

Последнее выражение можно переписать в виде: , где  амплитуда ЭДС индукции.

С помощью контактных колец и скользящих по ним щеток концы рамки соединяют с электрической цепью, в которой под действием ЭДС индукции, изменяющейся со временем по гар­моническому закону, возникнет переменный ток такой же частоты. Напряжение на выходных зажимах генератора несколько меньше ЭДС (на величину напряжения на внутреннем сопротивлении  см. раздел 2.2): и также изменяется по гармоническому закону и=U_msin(t). Мгновенное значение силы тока в цепи будет равно: , где I_m, - амплитуда колебаний тока,  - разность фаз между колебаниями тока и напряжения. Амплитуда тока и разность фаз зависят от характера сопротивления цепи.

6.2. Активное, емкостное, индуктивное сопротивление

Рис. 6.2. Резистор в цепи переменного тока. Ток и напряжение колеблются в одинаковой фазе

Активным называется сопротивление, в котором выделяется энергия тока. Таким сопротивлением обладает обычный проводник – резистор. Пусть через резистор (рис. 6.2), подключенный к генератору переменного тока (изображен символом ), протекает ток, изменяющийся по закону . Применим к участку цепи 1,2 закон Ома для мгновенных значений тока и напряжения в виде: . Получаем выражение: , из которого следует, что колебания напряжения на активном сопротивлении совпадают с колебаниями тока по фазе (рис.6.2), так как  = 0. Выражение , стоящее перед знаком синуса, есть амплитуда напряжения . Отсюда следует закон Ома для амплитудных значений:

. (6.1)

Мощность, выделяемая в резисторе, равна: . Это мгновенная мощность, зависящая от времени. Она положительна, поскольку в нее входит . Среднее значение равно ½, поэтому средняя мощность (за период) выразится как:

.

Рис. 6.3. Конденсатор в цепи переменного тока. Колебания тока опережают колебания напряжения на угол /2

(Четверть периода)

Действующим (эффективным) значением силы тока называют величину постоянного тока, который на активном сопротивлении за то же время выделяет такое же количество теплоты, как и данный переменный ток. Действующее значение силы тока связано с амплитудным значением соотношением: . Аналогично определяется действующее значение напряжения: . Использование действующих значений приводит полученные выше формулы для мощности к виду (2.17)  такому же, как для постоянного тока. Отметим, что в законе Ома для амплитуд (6.1) можно использовать и действующие значения тока и напряжения (естественно, одновременно).

Рассмотрим конденсатор в цепи переменного тока (рис. 6.3). Постоянный ток не протекает через конденсатор, поскольку тот фактически разрывает цепь постоянного тока. Однако при возникновении колебаний напряжения на конденсаторе происходит его перезарядка и в подводящих проводах возникают колебания тока. Пусть заряд на конденсаторе меняется по гармоническому закону: .

Сила тока является производной заряда по времени:

.

Следовательно, колебания силы тока опережают колебания напряжения на конденсаторе на /2. Амплитуда силы тока равна . Если ввести емкостное сопротивление , то из последнего выражения можно получить закон Ома для амплитуд:

(6.2)

Если вместо амплитудных значений использовать действующие, то получим закон Ома для действующих значений:

.

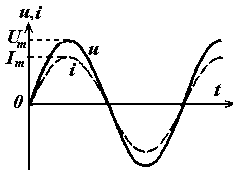
Рис. 6.4. Индуктивность в цепи переменного тока. Ток отстает от напряжения на угол /2

Индуктивность в цепи переменного тока (рис. 6.4) тоже влияет на величину тока, так как возникает ЭДС самоиндукции. Если активным сопротивлением катушки можно пренебречь, то разность потенциалов на катушке равна . Если ток в цепи меняется по закону , то

Колебания силы тока в катушке отстают от колебаний напряжения на /2. Амплитуда напряжения . Амплитудные (и действующие) значения тока и напряжения также связаны между собой законом Ома:

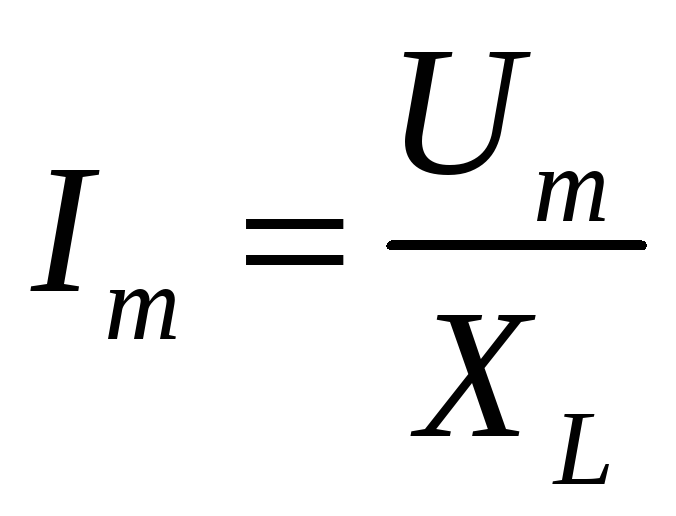, (6.3)

где  индуктивное сопротивление.

Мгновенное значение мощности переменного тока равно произведению мгновенных значений силы тока и напряжения:

.

Мгновенная мощность колеблется с удвоенной частотой, принимая как положительные, так и отрицательные значения. В эти моменты (когда мощность отрицательна) цепь отдает мощность внешнему источнику. Практический интерес представляет среднее за период значение мощности:

, (6.4)

или через действующие значения тока и напряжения:

. (6.5)

Косинус угла сдвига фаз между током и напряжением называют коэффициентом мощности.

Если в электрической цепи не совершается работа, средняя мощность выделяется в активном сопротивлении в виде тепла. Чем меньше cos, тем при большем токе выделится заданная мощность. Большие значения тока приводят к бесполезной потере мощности в соединительных проводах, поэтому на практике стараются увеличить коэффициент мощности нагрузки.

При сдвиге фаз =/2 (как в конденсаторе или катушке индуктивности без активного сопротивления) средняя выделяемая мощность равна нулю. Поэтому сопротивления X_С, X_L называются реактивными.