1. Радианая мера угла. Синус, косинус, тангенс и котангенс.

Углом в 1 радиан называется такой центральный угол, длина дуги которого равна радиусу окружности.

sin – отношение ординаты к радиусу

cos – отношение абсциссы к радиусу

tg – отношение ординаты к абсциссе

ctg – отношение абсциссы к ординате

2. Основные тригонометрические тождества

• sin² α + cos² α = 1

• tg α · ctg α = 1

• tg α = sin α ÷ cos α

• ctg α = cos α ÷ sin α

• 1 + tg² α = 1 ÷ cos² α

• 1 + ctg² α = 1 ÷ sin² α

3. Основные формулы тригонометрии Формулы сложения

• sin (α + β) = sin α · cos β + sin β · cos α

• sin (α - β) = sin α · cos β - sin β · cos α

• cos (α + β) = cos α · cos β - sin α · sin β

• cos (α - β) = cos α · cos β + sin α · sin β

• tg (α + β) = (tg α + tg β) ÷ (1 - tg α · tg β)

• tg (α - β) = (tg α - tg β) ÷ (1 + tg α · tg β)

Формулы двойного угла

• cos 2α = cos² α - sin² α

• cos 2α = 2cos² α - 1

• cos 2α = 1 - 2sin² α

• sin 2α = 2sin α · cos α

• tg 2α = (2tg α) ÷ (1 - tg² α)

Формулы суммы и разности синусов, косинусов

4.Числовая функция. Преобразование графиков.

Числовой функцией с областью определения D называется соответствие, при котором каждому числу Х из множества D сопоставляется по некоторому правилу число У, зависящее от Х.

Преобразование графиков функций

Функция	Преобразование графика функции
	Параллельный перенос вдоль оси OY на A единиц вверх, если А>0, и на |A| единиц вниз, если А<0.
	Параллельный перенос вдоль оси OX на a единиц вправо, если a > 0, на |a| единиц влево, если a < 0.
	Растяжение вдоль оси OY относительно оси OX в k раз, если k > 1, и сжатие в 1/kраз, если 0 < k < 1.
	Сжатие вдоль оси OX относительно оси OY в k раз, если k > 1, и растяжение в 1/kраз, если 0 < k < 1.
	Симметричное отражение относительно оси OX
	Часть графика, расположенная ниже оси OX, симметрично отражается относительно этой оси, остальная его часть остается без изменения.
	Симметричное отражение относительно оси OY.
	Часть графика, расположенная в области x  0, остается без изменения, а его часть для области x  0 заменяется симметричным отображением относительно оси OY части графика для x  0.

5.Четные и нечетные функции. Периодические функции.

Функция f называется четной, если для любого х из области определения f(-х)= f(x)

Функция f называется нечетной, если для любого х из области определения f(-х)=- f(x)

Функцию f называют периодической с периодом Т=0, если для любого х из области определения значения этой функции в точках х, х-Т и х+Т равны, т.е. f(x+T)=f(x)=f(x-T).

6. Возрастание и убывание функций. Экстремумы.

Функция f возрастает на множестве Р, если для любых x₁ и x₂ из множества Р, таких, что x₂ > x₁ , выполнено неравенство f(x₂) > f(x₁) .

Функция f убывает на множестве Р, если для любых x₁ и x₂ из множества Р, таких, что x₂ > x₁ , выполнено неравенство f(x₂) < f(x₁) .

Экстремумы – точки минимума и точки максимума.

7.Тригонометрическая функция y=sin x: определение, свойства и график.

Синусом  аргумента х (sin(x)) называется ордината точки пересечения окружности единичного радиуса с центром в начале координат и луча, выходящего из начала координат и составляющего с осью ОХ угол х. Областью определения функции sin(x) является вся числовая прямая - промежуток (-?;+?). Область значений лежит в промежутке [-1;1]. Функция sin(x)  периодична, период Т = 2П. Функция sin(x)  является нечетной, так как sin(-x)=-sin(x). График функции sin(x) называют синусоидой.  Синусоида пересекает ось ОХ в точках (kП;0). Синусоида имеет экстремумы-максимумы в точках  и экстремумы-минимумы в точках . График синусоиды:

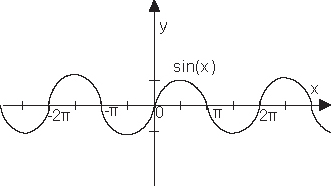
8.Тригонометрическая функция y=cos x: определение, свойства и график

Косинусом  аргумента х (cos(x)) называется абсцисса точки пересечения окружности единичного радиуса с центром в начале координат и луча, выходящего из начала координат и составляющего с осью ОХ угол х. Областью определения функции cos(x) является  вся числовая прямая - промежуток (-?;+?). Область значений лежит в промежутке [-1;1]. Функция cos(x) периодична, период Т = 2П. Функция cos(x) является четной, так как cos(-x)=cos(x). График функции cos(x), называют косинусоидой.  Косинусоида пересекает ось ОХ в точках .  Синусоида имеет экстремумы-максимумы в точках (2Пk;1) и экстремумы-минимумы в точках (П+2Пk;-1) График косинусоиды:

9.Тригонометрическая функция y=tg x: определение, свойства и график.

Тангенсом называется соотношение . Областью определения функции tg(x) является  вся числовая прямая , кроме точек  - в этих точках функция не определена, так как, по определению , а в точках . А на ноль делить нельзя. Область значений лежит в промежутке (-?;+?). Функция tg(x) периодична, период Т = П. Прямые  являются асимптотами. На каждом из промежутков  функция возрастает. График функции tg(x), называют тангенсоидой.  Тангенсоида пересекает ось ОХ в точках ,  График тангенсоиды:

10.Тригонометрическая функция y=ctg x: определение, свойства и график.

Котангенсом называется соотношение . Областью определения функции ctg(x) является  вся числовая прямая, кроме точек  - в этих точках функция не определена, так как, по определению , а в точках . А на ноль делить нельзя. Область значений лежит в промежутке (-?;+?). Функция ctg(x) периодична, период Т = П. Прямые  являются асимптотами. На каждом из промежутков  функция убывает. График функции ctg(x) называют котангенсоидой.  Котангенсоида пересекает ось ОХ в точках . График котангенсоиды:

11.Арксинус, арккосинус, арктангенс. Решение простейших тригонометрических уравнений.

Арксинусом числа а называется такое число из отрезка, синус которого равен а.

Арккосинусом числа а называется такое число из отрезка , косинус которого равен а.

Арктангенсом числа а называется такое число из отрезка, тангенс которого равен а.

12.Решение тригонометрических уравнений (на конкретных примерах)

13.Решение простейших тригонометрических неравенств (на конкретных примерах).

1. .Приращение функции. Понятие о касательной к графику функции. Мгновенная скорость движения. Производная.

∆x= x-x₀

∆f= f(x₀ +∆x) – f(x₀ )

Проходящую через точку (x₀;f (x₀;)) прямую, с отрезком которой практически сливается график функции f при значениях х, близких к x0, называют касательной к графику функции f в точке (х₀; f (х₀)).

Значение средней скорости при Δt→0 стремится к некоторому вполне определенному значению, которое и называют мгновенной скоростью v (t₀) материальной точки в момент времени to. Итак,

 при 

Производной функции f в точке x_0. называется число, к которому стремится разностное отношение

2.Правила вычисления производных.

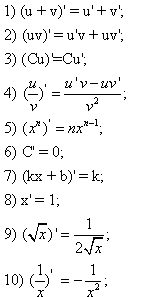
3.Производная сложной функции. Производные тригонометрических функций.

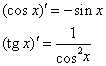
4.Применения непрерывности. Метод интервалов.

Если на интервале (a;b) функция f непрерывна и не обращается в нуль, то она на этом интервале сохраняет постоянный знак.

Метод интервалов

1.находим область допустимых значений (ОДЗ)

2. находим нули функции f(x) =0

3. отмечаем нули на ОДЗ и находим знак в каждом интервале.

4. записываем ответ, учитывая знак неравенства.

5.Касательная к графику функции.

y=f(x₀ ) –f/( x₀ )(x- x₀) Формула Лагранжа.

6.Признак возрастания (убывания) функции.

Признак возрастания: если f/(x) >0 в каждой точке интервала I, то функция является возрастающей.

Признак убывания: еслиf/(x) < 0 в каждой точке интервала I, то функция является убывающей.

7.Критические точки функции, максимумы и минимумы.

Если точка x₀ является точкой экстремума функции f и в этой точке существует производная f/, то она равна нулю: f/( x₀ )=0.

Если функции f непрерывна в точке x_0. , а f/(x) >0 на интервале (а; x₀ ) и f/(x) < 0 на интервале (x_0. ; b), то точка x_0. является точкой максимума функции f.

Если функции f непрерывна в точке x_0. , а f/(x) < 0 на интервале (а; x₀ ) и f/(x) > 0 на интервале (x_0. ; b), то точка x_0. является точкой минимумафункции f.