
- •6.170103 "Управління інформаційною безпекою" Затверджено
- •Вступ Нехай задане рівняння
- •Методи уточнення коренів нелінійних рівнянь Метод поділу проміжку навпіл
- •Значення е задається в межах 10 –410 –6.
- •Метод хорд
- •Комбінований метод хорд та дотичних
- •Метод простої ітерації
- •Метод Ейткена – Стефенсона
- •Метод Стефенсона
- •Завдання до лабораторної роботи
- •2.1. Домашня підготовка до роботи
- •2.2. Робота в лабораторії
- •Контрольні запитання
- •"Комп’ютерні методи дослідження інформаційних процесів та систем"
- •6.170103 "Управління інформаційною безпекою"
МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ
НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ "ЛЬВІВСЬКА ПОЛІТЕХНІКА"
МЕТОДИ УТОЧНЕННЯ КОРЕНІВ
НЕЛІНІЙНИХ РІВНЯНЬ
Методичні вказівки
до лабораторної роботи № 1
з курсу
"Комп’ютерні методи дослідження інформаційних процесів та систем"
для студентів базових напрямів 6.170101 "Безпека інформаційних і комунікаційних систем", 6.170102 "Системи технічного захисту інформації",
6.170103 "Управління інформаційною безпекою" Затверджено
на засіданні кафедри
«Безпека інформаційних технологій»
Протокол № 12 від 12.05.2011р.
Львів – 2011
Методи уточнення коренів нелінійних рівнянь: Методичні вказівки до лабораторної роботи №1 з курсу "Комп’ютерні методи дослідження інформаційних процесів та систем" для студентів базових напрямів 6.170101 "Безпека інформаційних і комунікаційних систем", 6.170102 "Системи технічного захисту інформації", 6.170103 "Управління інформаційною безпекою" /Укл.: Л.В. Мороз, А.Я. Горпенюк, Н.М. Лужецька - Львів: Видавництво НУ “ЛП”, 2011.- 18 с.
Укладачі: Л.В. Мороз, к.т.н., доц.
А.Я. Горпенюк, к.т.н., доц.
Н.М. Лужецька, асист.
Відповідальний за випуск: В.М. Максимович, д.т.н., проф.
Рецензенти: В.В. Хома, д.т.н., проф.,
А.Е. Лагун, к.т.н., доц.
Мета роботи – ознайомлення з методами уточнення коренів нелінійних рівнянь з одним невідомим.
Вступ Нехай задане рівняння
![]() , (1)
, (1)
де
![]() – неперервна функція.
Необхідно знайти всі або деякі корені
рівняння (1).
– неперервна функція.
Необхідно знайти всі або деякі корені
рівняння (1).
Подібна задача розв’язується за два етапи.
Перший
етап. На
цьому етапі розв’язується
задача відокремлення коренів нелінійного
рівняння. Задача полягає у виокремленні
достатньо малої області, що належить
області допустимих значень функції
![]() ,
у якій існує один і тільки один корінь
рівняння (1).
,
у якій існує один і тільки один корінь
рівняння (1).
Відокремлення
або ізоляція коренів рівняння (1)
грунтується на теоремі Больцано-Коші:
якщо неперервна функція
![]() на кінцях відрізка
на кінцях відрізка
![]() має різні за знаком значення, тобто
має різні за знаком значення, тобто
![]() ,
то на цьому
відрізку рівняння (1) має хоча б один
корінь. Якщо крім цього похідна
,
то на цьому
відрізку рівняння (1) має хоча б один
корінь. Якщо крім цього похідна
![]() існує і зберігає знак на відрізку
існує і зберігає знак на відрізку
![]() ,
тобто
,
тобто
![]() ,
або
,
або
![]() ,
то корінь єдиний.
,
то корінь єдиний.
Задача
ізоляції коренів нелінійного рівняння
(1) вирішується шляхом табулювання
функції
![]() або графічно
- шляхом побудови графіку функції
або графічно
- шляхом побудови графіку функції
![]() і визначення за графіком відрізків, на
яких локалізовано корені рівняння (1).
Графік функції як правило будують
приблизно із застосуванням методів
математичного аналізу.
і визначення за графіком відрізків, на
яких локалізовано корені рівняння (1).
Графік функції як правило будують
приблизно із застосуванням методів
математичного аналізу.
Результати першого етапу є вихідними даними для задачі уточнення коренів нелінійного рівняння.
Другий етап. Уточнення наближеного розв’язку до заданої точності.
Вихідними
даними для задачі уточнення кореня є
рівняння (1) і відрізок
![]() .
Відомо, що функція
.
Відомо, що функція
![]() має різні знаки на кінцях цього проміжку,
тобто виконується умова
має різні знаки на кінцях цього проміжку,
тобто виконується умова
![]() (2)
(2)
Крім
того,
![]() та
та
![]() – неперервні і зберігають знак на
проміжку
– неперервні і зберігають знак на
проміжку
![]() .
Необхідно знайти корінь рівняння (1) із
заданою граничною абсолютною похибкою
Е.
.
Необхідно знайти корінь рівняння (1) із
заданою граничною абсолютною похибкою
Е.
Поширеними методами розв’язку цієї задачі є метод поділу проміжку навпіл, метод хорд, метод Ньютона (дотичних), комбінований метод хорд та дотичних, метод простої ітерації, метод Ейткена–Стефенсона і метод Стефенсона.
-
Методи уточнення коренів нелінійних рівнянь Метод поділу проміжку навпіл
Цей метод відомий також за назвами методу бісекцій або методу дихотомії. Це простий і надійний алгоритм уточнення коренів рівняння (1).
Суть
методу полягає в тому, що відрізок
![]() ділиться навпіл, тобто вибирається
перше наближення кореня (Рис.1):
ділиться навпіл, тобто вибирається
перше наближення кореня (Рис.1):
![]() (3)
(3)
Якщо
![]() ,
тоді
,
тоді
![]() є коренем
рівняння (1).
є коренем
рівняння (1).

Рис.1.
Якщо
![]() ,
то вибирають той з відрізків
,
то вибирають той з відрізків
![]() чи
чи
![]() ,
на кінцях якого функція має різні знаки.
Обраний відрізок знову ділять навпіл
і т.д. Процес обчислень проводиться
доти, доки величина відрізку
,
на кінцях якого функція має різні знаки.
Обраний відрізок знову ділять навпіл
і т.д. Процес обчислень проводиться
доти, доки величина відрізку
![]() не стане меншою від заданої похибки Е.
не стане меншою від заданої похибки Е.
Метод досить стійкий до похибок заокруглень. Але й збігається теж повільно. При збільшенні точності значно зростає об’єм обчислень. Тому на практиці метод часто використовують для грубого визначення початкового наближення кореня, а далі застосовують швидко збіжний ітераційний метод.
Метод бісекцій збігається для будь-яких неперервних функцій. Кількість ітерацій, необхідних для досягнення точності E, оцінюють співвідношенням:
![]()
Алгоритм методу половинного ділення.
-
Задати значення параметрів а, b та граничної абсолютної похибки Е .
-
Обчислити значення функцій
 в точці а,
тобто обчислити
в точці а,
тобто обчислити
 .
. -
Поділити проміжок
 навпіл,
тобто знайти точку
навпіл,
тобто знайти точку
 :
:
 .
. -
Перевірити умову
 ?
Якщо так, то перейти до п.7.
?
Якщо так, то перейти до п.7. -
Якщо добуток
 ,
то
,
то
 ,
в протилежному випадку
,
в протилежному випадку
 .
. -
Якщо
 ,
то перейти до п.3.
,
то перейти до п.3. -
Надрукувати (вивести) значення
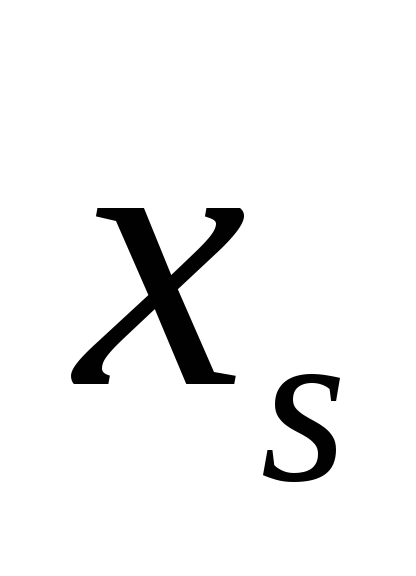 .
. -
Закінчити виконання програми.
