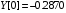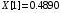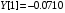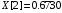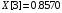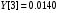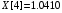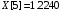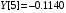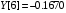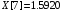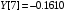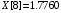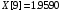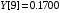lab10 / report_lab10
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра математического обеспечения и применения ЭВМ
отчет
по практической работе № 10
по дисциплине «Вычислительная математика»
Тема: Использование интерполяционной формулы в вычислении значения заданной функции
|
Студент гр. 7777 |
|
|
|
Преподаватель |
|
|
Санкт-Петербург
2018
Цель работы.
Необходимо разработать программу, обеспечивающую вычисление значения функции в заданных точках с использованием подходящих для каждого конкретного случая интерполяционных формул.
Основные теоретические положения.
Пусть величина
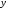 является функцией аргумента
является функцией аргумента
 .
Это означает,
что любому значению
.
Это означает,
что любому значению
 из области определения поставлено в
соответствие значение
из области определения поставлено в
соответствие значение
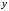 .
Однако на практике часто неизвестна
связь между
.
Однако на практике часто неизвестна
связь между
 и
и
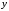 ,
т. е. невозможно записать эту связь в
виде некоторой зависимости
,
т. е. невозможно записать эту связь в
виде некоторой зависимости
 .
В других случаях при известной зависимости
.
В других случаях при известной зависимости
 её использование в практических задачах
затруднительно.
её использование в практических задачах
затруднительно.
Наиболее
распространённым и важным для практического
использования случаем, когда вид связи
между параметрами
 и
и
 неизвестен, является задание этой связи
в виде некоторой таблицы
неизвестен, является задание этой связи
в виде некоторой таблицы
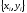 ,
в которой дискретному множеству значений
аргумента
,
в которой дискретному множеству значений
аргумента
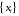 поставлено в соответствие множество
значений функции
поставлено в соответствие множество
значений функции
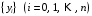 .
Эти значения – либо результаты расчётов,
либо экспериментальные данные. На
практике могут понадобиться значения
величины
.
Эти значения – либо результаты расчётов,
либо экспериментальные данные. На
практике могут понадобиться значения
величины
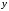 и в других точках, отличных от узлов
и в других точках, отличных от узлов
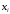 .
Таким образом, приходим к необходимости
использования имеющихся табличных
данных
для приближенного вычисления
искомого параметра
.
Таким образом, приходим к необходимости
использования имеющихся табличных
данных
для приближенного вычисления
искомого параметра
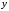 при любом значении определяющего
параметра
при любом значении определяющего
параметра
 ,
поскольку точная связь
,
поскольку точная связь
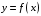 неизвестна.
неизвестна.
Этой цели
служит задача о приближении (аппроксимации)
функций:
данную функцию
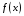 требуется аппроксимировать (приближённо
заменить) некоторой функцией
требуется аппроксимировать (приближённо
заменить) некоторой функцией
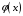 так, чтобы отклонение
так, чтобы отклонение
 от
от
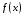 в заданной области было наименьшим.
Функция
в заданной области было наименьшим.
Функция
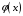 при этом называется аппроксимирующей.
при этом называется аппроксимирующей.
Для практики важен случай аппроксимации функции многочленом
 (1)
(1)
Этот случай,
т.е. приближение многочленами, является
одной из задач классического численного
анализа. Рассмотрим аппроксимацию этого
рода
и методы её реализации в
вычислительных процедурах на ЭВМ.
Коэффициенты
 в процедурах подбираются так, чтобы
достичь наименьшего отклонения многочлена
от данной функции.
в процедурах подбираются так, чтобы
достичь наименьшего отклонения многочлена
от данной функции.
Если приближение
строится на заданном дискретном множестве
точек
 ,
то аппроксимация называется точечной.
Одним из основных типов точечной
аппроксимации является интерполирование,
которое заключается
в следующем: для
функции
,
то аппроксимация называется точечной.
Одним из основных типов точечной
аппроксимации является интерполирование,
которое заключается
в следующем: для
функции
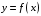 строится многочлен (1), принимающий в
заданных точках
строится многочлен (1), принимающий в
заданных точках
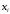 те же значения
те же значения
 ,
что и функция
,
что и функция
 ,
т.е.
,
т.е.
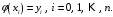 (2)
(2)
При данной
постановке задачи предполагается, что
среди значений
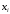 нет одинаковых:
нет одинаковых:
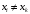 при
при
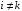 .
Точки
.
Точки
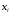 называются узлами интерполяции,
а
многочлен
называются узлами интерполяции,
а
многочлен
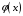 – интерполяционным многочленом. Близость
интерполяционного многочлена к заданной
функции состоит, таким образом,
в том,
что их значения совпадают на заданной
системе точек (узлов).
– интерполяционным многочленом. Близость
интерполяционного многочлена к заданной
функции состоит, таким образом,
в том,
что их значения совпадают на заданной
системе точек (узлов).
Максимальная
степень интерполяционного многочлена
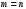 .
В этом случае говорят о глобальной
интерполяции, так как один многочлен
.
В этом случае говорят о глобальной
интерполяции, так как один многочлен
 (3)
(3)
используется для интерполяции функции
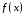 на всем рассматриваемом интервале
изменения аргумента
на всем рассматриваемом интервале
изменения аргумента
 .
Коэффициенты
.
Коэффициенты
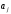 многочлена (3) находят
из системы
уравнений (2). Можно показать, что при
многочлена (3) находят
из системы
уравнений (2). Можно показать, что при
 (
( )
эта система имеет единственное решение.
)
эта система имеет единственное решение.
Возможны два
случая задания функции
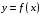 :
:
-
Точки
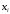 располагаются на оси абсцисс неравномерно
на различных расстояниях одна от другой
– случай неравноотстоящих узлов;
располагаются на оси абсцисс неравномерно
на различных расстояниях одна от другой
– случай неравноотстоящих узлов; -
Точки
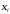 располагаются на оси абсцисс равномерно
с фиксированным шагом – случай
равноотстоящих узлов.
располагаются на оси абсцисс равномерно
с фиксированным шагом – случай
равноотстоящих узлов.
Если значения
функции
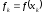 заданы в точках
заданы в точках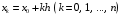 с постоянным положительным шагом, то
часто используется интерполяционный
многочлен Ньютона для интерполяции
вперёд
с постоянным положительным шагом, то
часто используется интерполяционный
многочлен Ньютона для интерполяции
вперёд
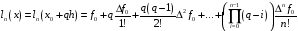 , (4)
, (4)
где
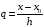 ,
а конечные разности
,
а конечные разности
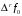 ,
носящие названия нисходящих разностей,
находят из соотношений
,
носящие названия нисходящих разностей,
находят из соотношений
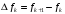 ,
,
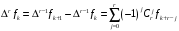 .
.
Интерполяционный
многочлен (4) удобно использовать при
работе
в начале таблицы значений
функции и для экстраполяции левее точки
 .
.
Интерполяционный
многочлен с узлами
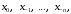 где
где
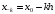 ,
имеет вид
,
имеет вид
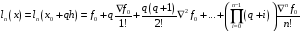 (5)
(5)
и называется интерполяционным многочленом
Ньютона для интерполяции назад. Его
удобно использовать при интерполяции
в конце таблицы
и для экстраполяции
правее точки
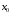 .
Входящие в выражение (5) значения конечных
восходящих разностей находят из
соотношений
.
Входящие в выражение (5) значения конечных
восходящих разностей находят из
соотношений
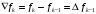 ,
,
..............................................
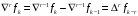 .
.
Если при
заданном
 в таблице значений функции
в таблице значений функции
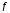 с шагом
с шагом
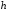 имеется достаточное число узлов с каждой
стороны от
имеется достаточное число узлов с каждой
стороны от
 ,
то целесообразно узлы интерполяции
,
то целесообразно узлы интерполяции
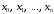 выбрать так, чтобы точка
выбрать так, чтобы точка
 оказалась как можно ближе к середине
минимального отрезка, содержащего узлы.
При этом обычно
в качестве
оказалась как можно ближе к середине
минимального отрезка, содержащего узлы.
При этом обычно
в качестве
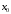 берётся ближайший к
берётся ближайший к
 узел, затем за
узел, затем за
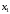 принимается ближайший к
принимается ближайший к
 узел, расположенный с противоположной
от
узел, расположенный с противоположной
от
 стороны, чем
стороны, чем
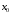 .
Следующие узлы назначаются поочерёдно
с разных сторон от
.
Следующие узлы назначаются поочерёдно
с разных сторон от
 и должны быть расположены как можно
ближе к
и должны быть расположены как можно
ближе к
 .
Одной из возможных схем интерполяции
в этом случае является схема Стирлинга
с интерполяционным многочленом вида
.
Одной из возможных схем интерполяции
в этом случае является схема Стирлинга
с интерполяционным многочленом вида

В этом выражении
учитывается, что дано нечётное число
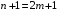 значений функции
значений функции
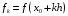 ,
где
,
где
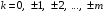 .
Обычно эту формулу целесообразно
использовать при
.
Обычно эту формулу целесообразно
использовать при
 .
.
Постановка задачи.
Используя
подходящую интерполяционную формулу,
вычислить в точках
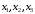 значения функции, по заданным равноотстоящим
узлам, заданным
табл. 1.
значения функции, по заданным равноотстоящим
узлам, заданным
табл. 1.
Исходные данные:
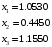
Таблица 1 – Значения функции в точках.
|
Значение узла |
Значение функции в данном узле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Порядок выполнения, следующий:
-
Составить вспомогательные функции для часто используемых вычислений.
-
Составить функции для вычисления значений функции с помощью интерполяционного многочлена Ньютона для интерполяции назад и вперёд, и схемы Стирлинга.
-
Составить головную программу, содержащую обращение к вычислительным процедурам и осуществляющую печать результатов.
-
Объявить исходные данные в программе.
-
Провести вычисления по программе.
Выполнение работы.
Были составлены вспомогательные функции для вычислений, а также функции для вычисления интерполяционного многочлена Ньютона для интерполяции вперёд и назад, и схемы Стирлинга. Также была написана головная программа, содержащая обращение к вычислительным процедурам и выводящая результат. Были объявлена исходные данные программы Код данной программы приведен в приложении A.
Были выбраны
методы для вычисления каждого
 .
С помощью схемы Стирлинга рассчитаем
.
С помощью схемы Стирлинга рассчитаем
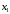 и
и
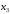 т.к. значения лежат близко к центру
таблицы. А
т.к. значения лежат близко к центру
таблицы. А
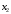 находить близко к началу таблицы,
следовательно выбираем интерполяционный
многочлен Ньютона для интерполяции
вперёд.
находить близко к началу таблицы,
следовательно выбираем интерполяционный
многочлен Ньютона для интерполяции
вперёд.
В результате вычислений были получены следующие значения:
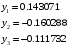
Выводы.
Были написаны
функции для вычисления значения функции
в точке
 c
помощью интерполяционного многочлена
Ньютона для интерполяции вперёд и назад
и схемы Стирлинга. В результате работы
были вычислены значения функции в точках
c
помощью интерполяционного многочлена
Ньютона для интерполяции вперёд и назад
и схемы Стирлинга. В результате работы
были вычислены значения функции в точках
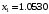 ,
,
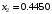 ,
,
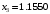 методами подходящими к данным точкам
методами подходящими к данным точкам
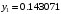 ,
,
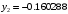 ,
,
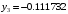 .
Проанализировав результаты работы
программы, мы можем сделать вывод, что
в том случае, если точка, значение функции
в которой нам необходимо найти, лежит
в конце таблицы задания функции, то для
решения задачи мы можем воспользоваться
интерполяционным многочленом Ньютона
для интерполяции назад. Если в начале
таблицы – интерполяционным многочленом
Ньютона для интерполяции вперёд. Если
же точка лежит в середине таблицы и
.
Проанализировав результаты работы
программы, мы можем сделать вывод, что
в том случае, если точка, значение функции
в которой нам необходимо найти, лежит
в конце таблицы задания функции, то для
решения задачи мы можем воспользоваться
интерполяционным многочленом Ньютона
для интерполяции назад. Если в начале
таблицы – интерполяционным многочленом
Ньютона для интерполяции вперёд. Если
же точка лежит в середине таблицы и
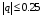 ,
то целесообразнее воспользоваться
схемой Стирлинга.
,
то целесообразнее воспользоваться
схемой Стирлинга.
ПРИЛОЖЕНИЕ А
КОД ПРОГРАММЫ
#include <cmath>
#include <iostream>
#define N 11
using namespace std;
const double X[] = { 0.3060, 0.4890, 0.6730, 0.8570, 1.0410, 1.2240, 1.4080 , 1.5920,1.7760, 1.9590 , 2.1430};
const double Y[] = { -0.2870, -0.0710, 0.0170, 0.0140, -0.0410, -0.1140, -0.1670, -0.1610, -0.0610, 0.1700, 0.5720 };
long factorial(int x){
if ((x == 1) || (x == 0)) return 1;
return x * factorial(x - 1);
}
double C(int j, int r){
return factorial(r) / (factorial(j) * factorial(r - j));
}
double down_difference(int r, int k) {
double S = 0;
for (int j = 0; j <= r; j++)
S += pow(-1, j)*C(j, r)*Y[k + r - j];
return S;
}
double up_difference(int r, int k){
return down_difference(r, k - r);
}
double back_Newton(double x, int n) {
double S = Y[n], q, Q;
q = (x - X[n]) / (X[1] - X[0]);
Q = q;
for (int i = 1; i <= n; i++) {
S += Q * up_difference(i, n) / factorial(i);
Q *= (q + i - 1);
}
return S;
}
double ahead_Newton(double x,int n){
double S = Y[0], q, Q;
q = (x - X[0]) / (X[1] - X[0]);
Q = q;
for (int i = 1; i <= n; i++) {
S += Q * down_difference(i, 0) / factorial(i);
Q *= (q - i + 1);
}
return S;
}
double difference_Stirling(int r, int k){
double S = 0;
for (int j = 0; j <= k; j++)
S += pow(-1, j)*C(j, k)*Y[k - j];
return S;
}
double Stirling(double x, int z,int n) {
double S, q, Q;
q = abs(x - X[z]) / (X[1] - X[0]);
S = Y[z];
Q = 1;
for (int i = 1; i <= n; i++) {
S += q * Q*(difference_Stirling(2 * i - 1, i) + difference_Stirling(2 * i, i - 1))
/ (factorial(2 * i - 1) * 2) + q * q*Q*difference_Stirling(2 * i, i) / factorial(2 * i);
Q *= (q*q - i + 1);
}
return S;
}
int main(){
double x1, x2, x3;
x1 = 1.0530;
x2 = 0.4450;
x3 = 1.1550;
cout << "Y1 = "<< Stirling(x1,6,N) << endl;
cout << "Y2 = " << ahead_Newton(x2,N) << endl;
cout << "Y3 = " << Stirling(x3,5,N) << endl;
}