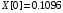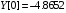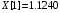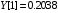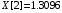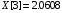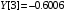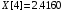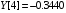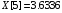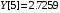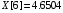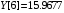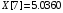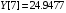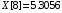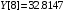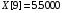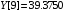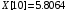lab9 / report_lab9

_{МИНОБРНАУКИ РОССИИ}

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра математического обеспечения и применения ЭВМ

отчет

по практической работе № 9

по дисциплине «Вычислительная математика»

Тема: САМОСТОЯТЕЛЬНАЯ РАЗРАБОТКА ПРОГРАММЫ НА ОДНОМ ИЗ ЯЗЫКОВ ПРОГРАММИРОВАНИЯ

Студент гр. 7777
Преподаватель

Санкт-Петербург

2018

Цель работы.

Используя интерполяционную схему Эйткена, либо интерполяционную формулу Ньютона, вычислить значение в точке x функции.

Основные теоретические положения.

Пусть известны значения некоторой функции 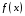в 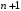различных точках 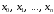, которые обозначим следующим образом: .

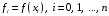Указанные значения могут быть получены путём экспериментальных измерений или найдены с помощью достаточно сложных вычислений. В задаче интерполяции функции 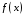, как было сказано ранее, решается проблема приближенного восстановления значения функции в произвольной точке x. Для этого строится алгебраический многочлен 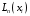степени n, который в точках 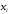принимает заданные значения, т. е.

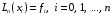. (1)

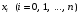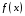Следует заметить, что если точка x расположена вне минимального отрезка, содержащего все узлы интерполяции , то замену функции на 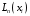также называют экстраполяцией.

В общем случае доказано, что существует единственный интерполяционный многочлен n-й степени, удовлетворяющий условиям (1):

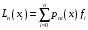, (2)

где

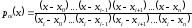(3)

Интерполяционный многочлен, представленный в виде (2), называется интерполяционным многочленом Лагранжа, а функции (3) – лагранжевыми коэффициентами.

Для оценки погрешности интерполяции (в частности, и экстраполяции) в текущей точке 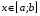( 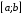– отрезок, содержащий все узлы интерполяции 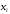и точку ) можно использовать соотношение

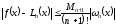, (4)

где 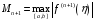; 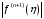– (n+1)-я производная интерполируемой функции в некоторой точке ; .

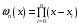Оценить максимальную погрешность интерполяции на всем отрезке 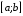можно с помощью соотношения

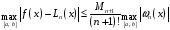. (5)

Использование оценок погрешностей (4) и (5) предполагает ограниченность 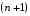-й производной интерполируемой функции на отрезк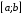е , т. е. .

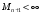На практике вместо общей формы записи (5) часто используются другие формы записи интерполяционного многочлена, более удобные для применения в конкретных ситуациях.

Интерполяционный многочлен Ньютона для неравноотстоящих узлов интерполяции имеет вид:

…

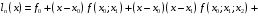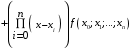…, (6)

где 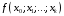– разделённая разность 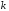-го порядка.

Вычисление разделённых разностей производится по соотношениям

,

...................................................

.

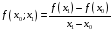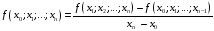При использовании интерполяционного многочлена Ньютона (6) изменение степени n требует только добавить или отбросить соответствующее число стандартных слагаемых, что удобно на практике. В то же время, непосредственное использование интерполяционного многочлена Лагранжа (2) требует строить его заново при изменении n.

В том случае, если требуется найти лишь численное значение интерполяционного многочлена 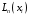, а не его представление, может быть использована итерационно-интерполяционная схема Эйткена.

Пусть 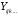- интерполяционный многочлен, определяемый парами 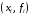, , , 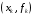... так, что .

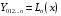Интерполяционные многочлены возрастающих степеней получают последовательно следующим образом:

,

,

...….....................................................

,

...….....................................................

.

...….....................................................

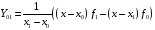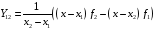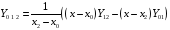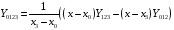Этот процесс можно закончить, когда у значений двух интерполяционных многочленов последовательных степеней совпадает требуемое количество знаков.

Постановка задачи.

Исходные данные: 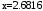, значения функции в точках приведены табл.1.

Таблица 1 – Значения функции в точках.

Порядок выполнения, следующий:

1. Составить программы-функции для вычисления значения функции в точке методом интерполяции.

2. Составить головную программу, содержащую обращение к вычислительным процедурам и осуществляющую печать результатов.

3. Результаты работы оформить в виде краткого отчёта, содержащего характеристику используемого метода вычислений, его точности и полученное значение функции.

Выполнение работы.

Были составлены функции для вычисления методом Ньютона и методом Эйткина. Также была написана головная программа, содержащая обращение к вычислительным процедурам и выводящую результат. Коды данных функций приведены в приложении A.

Были проведены вычисления по программе методами Эйткена и Ньютона:

Выводы.

Были написаны функции для вычисления значения функции в точке c помощью метода Ньютона и метода Эйткина. В результате работы были вычислены значения функции в точке 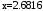методом Ньютона 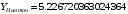и методом Эйткина 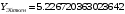. Оба метода дали очень точные и близкие значения, совпадающие до 11 знака после запятой. Таким образом можно сделать вывод ,что оба метода обладают хорошей точностью вычисления. Так же с помощью метода Ньютона был построен интерполяционный многочлен, и по нему было вычислено значение функции в точке . Метод Эйткина произвёл вычисление значения функции прямым вычислением. Для данной работы эффективнее использовать метод Эйткина для вычисления результата.

ПРИЛОЖЕНИЕ А

КОД РОГРОАММЫ

#include "pch.h"

#include <iostream>

#include <iomanip>

using namespace std;

const double X[] = { 0.1096, 1.1240, 1.3096, 2.4160, 3.6336, 4.6504, 5.0360, 5.3056,5.5000, 5.8064 };

const double Y[] = { -4.8652, 0.2038, 0.3613,-0.0606, -0.3440, 2.7259, 15.9677, 24.9477, 32.8147, 39.3750, 51.3433 };

double Eitken(int a, int b, double x){

const int n = 11;

if (b - a > n) exit(0);

if ((b - a) == 1){

return (1 / (X[b] - X[a])*((x - X[a])* Y[b] - (x - X[b])* Y[a]));

}else{

return (1 / (X[b] - X[a])*((x - X[a])*Eitken(a + 1, b, x) - (x - X[b])*Eitken(a, b - 1, x)));

}

return 0;

}

double int_Newton(double x){

const int n = 11;

double a, b;

int i, j, k;

double f[n][n];

for (i = 0; i < n; i++)

f[i][0] = (Y[i + 1] - Y[i]) / (X[i + 1] - X[i]);

for (j = 1; j < n; j++)

for (i = 0; i < (n - j ); i++)

f[i][j] = (f[i + 1][j-1] - f[i][j-1]) / (X[j + i + 1] - X[i]);

b = Y[0];

for (i = 1; i <= n; i++){

a = 1;

for (k = i; k > 0; k--)

a *= (x - X[k - 1]);

b+= f[0][i - 1] * a;

}

return (b);

}

int main(){

setlocale(LC_ALL, "Russian");

double x = 2.6816;

cout << "по Эйткину y = " << fixed << setprecision(15) <<Eitken(0,11,x)<<endl;

cout << "по Ньютону y = " << fixed << setprecision(15) << int_Newton(x) << endl;

}