lab7 / report_lab7

_{МИНОБРНАУКИ РОССИИ}

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра математического обеспечения и применения ЭВМ

отчет

по практической работе № 7

по дисциплине «Вычислительная математика»

Тема: Численное интегрирование

Студент гр. 7777
Преподаватель

Санкт-Петербург

2018

Цель работы.

Используя квадратурные формулы прямоугольников, трапеций и Симпсона, вычислить значения интеграла

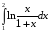(1)

и, применив правило Рунге, найти наименьшее значение (наибольшее значение шага 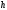), при котором каждая из указанных формул даёт приближенное значение интеграла с погрешностью , не превышающей заданную.

Основные теоретические положения.

Повышения точности численного интегрирования добиваются путём применения составных формул. Для этого при нахождении определённого интеграла отрезок 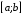разбивают на чётное 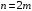число отрезков длины 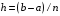и на каждом из отрезков длины 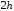применяют соответствующую формулу. Таким образом получают составные формулы прямоугольников, трапеций и Симпсона.

На сетке , , 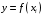, 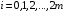составные формулы имеют следующий вид:

формула прямоугольников

;

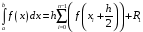формула трапеций

;

формула Симпсона

,

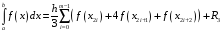где 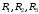– остаточные члены. При 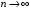приближенные значения интегралов для всех трёх формул (в предположении отсутствия погрешностей округления) стремятся к точному значению интеграла.

Для практической оценки погрешности квадратурной можно использовать правило Рунге. Для этого проводят вычисления на сетках с шагом и 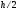, получают приближенные значения интеграла 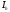и и за окончательные значения интеграла принимают величины:

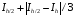- для формулы прямоугольников;

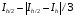- для формулы трапеций;

- для формулы Симпсона.

За погрешность приближенного значения интеграла для формул прямоугольников и трапеций тогда принимают величину , а для формулы Симпсона .

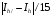Постановка задачи.

Порядок выполнения следующий:

1. Составить программы-функции для вычисления интегралов по формулам прямоугольников, трапеций и Симпсона.

2. Составить программу-функцию для вычисления подынтегральной функции.

3. Составить головную программу, содержащую оценку по Рунге погрешности каждой из перечисленных выше квадратурных формул, удваивающих до тех пор, пока погрешность не станет меньше , и осуществляющих печать результатов: значения интеграла и значения для каждой формулы.

4. Провести вычисления по программе, добиваясь, чтобы результат удовлетворял требуемой точности.

5. Результаты работы оформить в виде краткого отчёта, содержащего сравнительную оценку применяемых для вычисления формул.

Выполнение работы.

Были составлены функции для вычисления интегралов по формулам прямоугольников, трапеций и Симпсона, функция для вычисления подынтегральной функции. Также была написана головная программа, содержащая оценку погрешностей по Рунге. Коды данных функций приведены в приложении A.

Были проведены вычисления по программе, добиваясь, чтобы результат удовлетворял требуемой точности. Результат вычисления приведён в табл. 1.

Таблица 1 – Расчёт значения интеграла по формулам

Значение Eps	Тип расчёта интеграла	Значение интеграла I	Значение n
0,01	прямоугольник	-0,521554	2
	трапеция	-0,526673	2
	метод Симпсона	-0,523304	2
0,001	прямоугольник	-0,521554	2
	трапеция	-0,525739	3
	метод Симпсона	-0,523304	2
0,0001	прямоугольник	-0,523056	6
	трапеция	-0,523527	9
	метод Симпсона	-0,523273	2

Зависимость количества отрезков n от приведена на рис. 1.

Рисунок 1 – Зависимость n от

Выводы.

Проанализировав результаты работы программы, мы можем сделать вывод, что число итераций, необходимых для вычисления интеграла по составным формулам прямоугольника, трапеции и Симпсона возрастает с ростом требуемой точности результата. Исходя из результатов тестирования программы, мы можем сделать вывод, что меньше всего итераций для получения необходимой точности результата требуется при вычислении интеграла по формуле Симпсона, далее в порядке увеличения числа итераций идет формула прямоугольников, а затем формула трапеций.

ПРИЛОЖЕНИЕ А

КОД ПРОГРАММЫ

#include "pch.h"

#include <iostream>

#include <math.h>

#include<Windows.h>

using namespace std;

double F(double x) {

return log(x / (1 + x));

}

double rectangle(int n,double a,double b) {

double x,h,sum = 0;

h = (b-a) / n;

for (int i = 0; i < n; i++){

x = a + i * h;

sum += F(x + (h/2));

}

return sum * h;

}

double trapeze(int n, double a, double b) {

double x1,x2, h, sum = 0;

h = (b - a) / n;

for (int i = 0; i < n; i++) {

x1 = a + i * h;

x2 = a + (i + 1) * h;

sum += (F(x1) + F(x2));

}

return sum * h/2;

}

double Simpson_method(int n, double a, double b) {

double x1, x2,x3, h, sum = 0;

h = (b - a) / n;

int m = n / 2;

for (int i = 0; i < m; i++) {

x1 =a+ 2 * i * h;

x2 =a+ (2 * i +1) * h;

x3 = a+(2 * i + 2) * h;

sum += (F(x1) + 4 * F(x2) + F(x3));

}

return sum * h / 3;

}

int main(){

SetConsoleCP(1251);

SetConsoleOutputCP(1251);

double Ir, It, Is, epsR, epsT, epsS, eps;

int nr,nt, ns;

nr = nt = ns = 2;

cout << "I = ln (1/(1+x))dx на [a;b]" << endl;

double a = 1.0, b = 2.0;

cout << "Введите Eps:";

cin >> eps;

epsR = abs(rectangle(nr * 2, a, b) - rectangle(nr, a, b)) / 3;

while (epsR >= eps) {

nr ++;

epsR = abs(rectangle(nr * 2, a, b) - rectangle(nr, a, b)) / 3;

}

epsT = abs(trapeze(nt * 2, a, b) - trapeze(nt, a, b)) / 3;

while (epsT >= eps) {

nt ++;

epsT = abs(trapeze(nt * 2, a, b) - trapeze(nt, a, b)) / 3;

}

epsS = abs(Simpson_method(ns * 2, a, b) - Simpson_method(ns, a, b)) / 15;

while (epsS >= eps) {

ns += 2;

epsS = abs(Simpson_method(ns * 2, a, b) - Simpson_method(ns, a, b)) / 15;

}

Ir = rectangle(nr * 2, a, b) + epsR;

It = trapeze(nr * 2, a, b) - epsT;

Is = Simpson_method(nr * 2, a, b) - epsS;

cout << "Ir =" << Ir << " nr = " << nr << endl;

cout << "It =" << It << " nt = " << nt << endl;

cout << "Is =" << Is << " ns = " << ns << endl;

}