1.4 Метод узловых напряжений

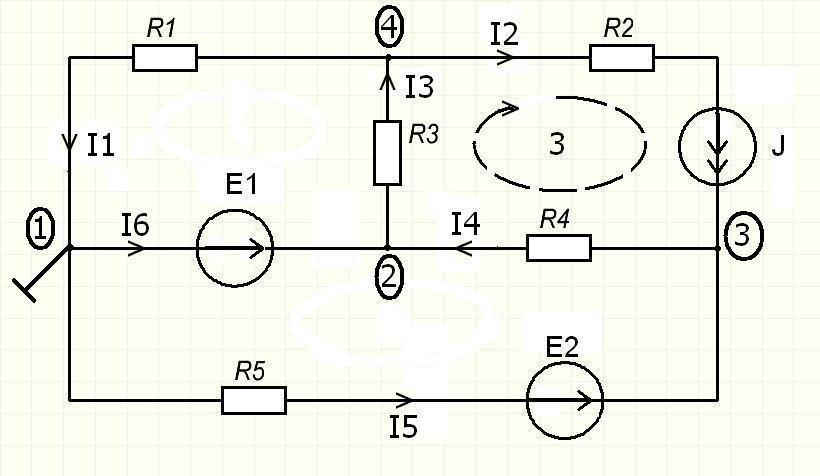
Рисунок 1.5– Схема для расчета методом узловых напряжений

Метод без преобразования схемы. Определение узловых потенциалов по уравнениям законов токов Кирхгофа. Определение токов в ветвях по закону Ома.

Алгоритм расчета:

1) Обозначаем все токи и узлы в схеме

2) Принимаем один из узлов за базисный (потенциал этого узла будет равен нулю)

3) Определяем собственные и взаимные проводимости узлов:

4) Составляем уравнения по МУН

5) Решив систему уравнений, найдем потенциалы узлов

(В)

6) Токи в схеме найдем по закону Ома:

Так как токи совпадают с токами, рассчитанными методом наложения и методом контурных токов - расчет верен.

1.5 Метод эквивалентного генератора

Рисунок 1.6 – Схема для расчета по МЭГ

Алгоритм расчета:

1) Обозначаем на схеме ток, который нужно найти, произвольно выбрав его направление

2) Обозначаем зажимы a и b сопротивления R, через который протекает искомый ток

3) Определяем эквивалентное сопротивление схемы относительно зажимов a и b, заменив источники на их внутреннее сопротивление:

Рисунок 1.17 - Схема для определения эквивалентного сопротивления

(1.41)

4) Определяем параметры эквивалентного источника тока:

4.1. Обозначим напряжение холостого хода , совпадающего по направлению с искомым током.

4.2. Рассчитаем полученную схему, определим U_хх

E_г = U_хх., R_г = R_экв

= -J = -10 (мА); (1.54)

Из (1.53) найдем

= 60 – (-10) 20 = 80 (В);

Теперь найдем искомый ток:

= (1.55)

Значение искомого тока совпало с его значениями в прошлых расчетах.

1.6 Баланс мощности

Сумма мощностей, отдаваемых независимыми источниками равна сумме мощностей, потребляемых остальными элементами электрической цепи.

Алгоритм расчета:

1) Определяем токи в схеме любым способом

2) Определяем мощности источников ЭДС

3) Определяем мощности источников тока (для этого нужно определить U_г)

4) Определяем мощность рассеяния на пассивных элементах схемы

5) Проверяем баланс равенство:

Если , значит токи в схеме рассчитаны верно.

Сумма мощностей, отдаваемых независимыми источниками, равна сумме мощностей, потребляемых остальными элементами электрической цепи, значит токи в схеме рассчитаны верно.

2.1 Матрично-топологический метод

В основе метода лежит представление электрической схемы с помощью графа цепи. Ветви ориентированного графа ориентированы по направлению тока ветвей.

Порядок расчета:

1. Обозначить токи в ветвях произвольным образом.

2. Составить граф схемы, задать направление обхода контуров.

3. По графу составить контурную матрицу В, в которой столбцы – ветви, а строки – контуры (если направление ветви совпадает с обходом контура ставим «1», если не совпадает «-1», если ветвь не принадлежит контуру ставим «0».

4. Составляем диагональную матрицу сопротивлений ветвей Z . Диагональные элементы матрицы - сопротивления соответствующих ветвей схемы; на пересечении k – ой строки и j – го столбца, а также j – ой строки k – го столбца записывается сопротивление взаимоиндукции между индуктивно – включенными в k – ую и j – ую строки катушками индуктивности.

5. Составляем матрицу ЭДС, записывая значение источников ЭДС в соответствующую строку матрицы.

6. Составляем матрицу токов, записывая значение источников тока в соответствующую строку матрицы.

7. Составляем матрицу контурных токов.

8. Рассчитаем матрицу контурных сопротивлений.

9.Рассчитаем матрицу контурных ЭДС.

10. Получим контурные токи.

Рисунок 2.1 – Исходная схема

Рисунок 2.2 – Схема с развязанным источником ЭДС

Уравнение электрического равновесия контурных токов:

[B] [Z_в] [B^т] [I_k] = [B] ([E] – [Z_в] ) (2.11)

Следует составить все матрицы, входящие в это уравнение, чтобы получить в итоге уравнения контурных токов.

Составим контурную матрицу- [B], диагональную матрицу сопротивлений ветвей- [], матрицу ЭДС- [E], матрицу токов- [I] и матрицу контурных токов- [];

Рассчитаем матрицу контурных ЭДС:

Расчитаем матрицу контурных сопротивлений:

;

Возьмем определитель матрицы сопротивлений ветвей:

Чтобы найти контурный ток заменим первый столбец матрицы

= 10j - 90 = 90; (2.25)

Проделаем то же самое, чтобы найти контурный ток

= -j60 = 60; (2.27)

Зная контурные токи, найдем искомые:

На этом расчёт цепи матрично-топологическим методом закончен.