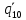- •1. Застосування теореми про зміну кінетичного моменту для визначення кутової швидкості твердого тіла
- •Малюнок 1
- •Малюнок 2
- •Малюнок 3
- •Малюнок 5
- •2. Застосування теореми про зміну кінетичної енергії для вивчення руху механічної системи
- •Малюнок 6
- •Малюнок 7
- •3. Визначення динамічних реакцій
- •Малюнок 7
- •4. Рівняння Лагранжа
- •Малюнок 9
3. Визначення динамічних реакцій
Тіло, що складається з пластини зі сторонами l3, l2, масою m2 та матеріальної точки m1 на стрижні довжиною l1, закріплених на валу АВ = L=1 м, обертається навколо нерухомої осі за законом φ(t), в якому прийнято ε=20 рад/с2 (рис 7). Використовуючи метод кінетостатики знайти динамічні та додаткові реакції в опорах вала, а у разі прискореного обертального руху, знайти ще й обертальний момент Mоб. Закон руху, маси та розміри тіл наведені у таблиці 3.
Малюнок 7
|
№ варіанту |
φ(t), рад |
m1 |
m2 |
l1 |
l2 |
l3 |
a |
b |
|
|
кг |
м |
|
|||||||
|
12 |
|
5 |
20 |
0.3 |
0.3 |
0.4 |
0.2 |
0.3 |
|
Таблиця 3
Спочатку визначимо динамічні реакції опор. Зв’яжемо жорстко з тілом рухому систему кординат Axyz. Визначимо активні сили m1g, m2g, що діють на тіло і Моб. Відповідно до аксіоми про звільнення від в’язей відкинемо верхню і нижню підшипникові опори і замінимо їх відповідними реакціями в’язей XA, YA, ZA, XB, YB. До центрів мас кожного з елементів, які складають тіло умовно прикладемо у напрямку, протилежному їх прискоренням (або складовим прискорень)
 Малюнок
8
Малюнок
8
 ,
,

 ,
,

Отримана система сил є довільною просторовою, тому використаємо відповідні умови її рівноваги:
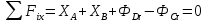 ,
(1)
,
(1)
 ,
(2)
,
(2)
 ,
(3)
,
(3)
 ,
(4)
,
(4)
 ,
(5)
,
(5)
 ,
(6)
,
(6)
Розв’яжемо ці рівняння відносно невідомих величин. З рівняння (6) знайдемо обертальний момент:

Із рівняння (4) отримуємо:
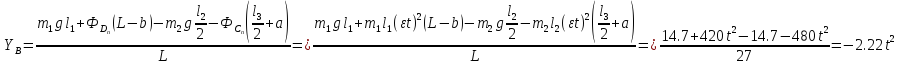
Із рівняння (5) отримуємо:

Далі з виразу (3) випливає, що:
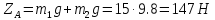
З
рівняння (1) знайдемо
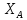
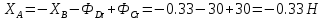
З рівняння (2) отримаємо:

Від’ємний
знак у виразах
 ,
,
 вказує на те, що вектори
вказує на те, що вектори
 ,
,
 мають протилежний напрям.
мають протилежний напрям.
Додаткові динамічні реакції отримаємо, залишивши у виразах повних реакцій лише ті члени, які залежать від ε та εt, а саме:
 Н
Н
 Н
Н
 Н
Н
4. Рівняння Лагранжа
Механічна система, що складається з п’яти тіл, рухається під дією сил ваги та пари сил з моментом M сталої величини. Дані для розв’язку подані в таблиці 4. Схема механізму зображена на рисунку 9. Знайти кінематичні рівняння руху системи в узагальнених координатах, які вказані в таблиці, використовуючи початкові умови.
Малюнок 9
|
Варіант |
Маси тіл |
Радіуси блоків |
Радіус інерції |
Узагальнені координати |
Початкові умови |
|||||||||||||||
|
m1 |
m2 |
m3 |
m4 |
m5 |
R1 |
r2 |
R2 |
R3 |
i2 |
q1 |
q2 |
q10 |
|
q20 |
|
|||||
|
12 |
2m |
3m |
m |
m |
0.5m |
2r |
r |
2r |
r |
r |
s3 |
x |
0 |
0 |
0 |
|
||||

Малюнок 10
Механічна система, рух якої досліджується, має два степені вільності, тому система рівнянь Лагранжа другого роду має вигляд

(1)

Де
Т
–
кінетична енергія системи,
 - потенціальна енергія,
- потенціальна енергія,

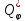 -
узагальнені сили, які мають потенціальний
характер.
-
узагальнені сили, які мають потенціальний
характер.
Визначимо
кінетичну енергію системи
 як функцію узагальнених координат і
швидкостей, де
як функцію узагальнених координат і
швидкостей, де
 - кінетична енергія окремих тіл.
- кінетична енергія окремих тіл.
Для блока 1 маємо:

Осьовий
момент інерції першого блока
 ,
кутову швидкість виразимо через
узагальнену координату
,
кутову швидкість виразимо через
узагальнену координату
 ,
отримаємо:
,
отримаємо:
 (2)
(2)
Для блоку 2 аналогічно

Осьовий
момент інерції другого блока
 .
Кутову швидкість виразимо через
узагальнену координату
.
Кутову швидкість виразимо через
узагальнену координату
 , оскільки R1
=
R2,
отримаємо:
, оскільки R1
=
R2,
отримаємо:
 (3)
(3)
Рух
тіла 4 можна подати як сукупність двох
поступальних рухів: переносного разом
з
центром мас блока 3 і руху
блока 3 відносно цього центра зі швидкістю
 .
Швидкість
.
Швидкість
 центра мас тіла 3 можна знайти на підставі
співвідношення:
центра мас тіла 3 можна знайти на підставі
співвідношення:
 (4)
(4)
Тоді абсолютна швидкість тіла 4:

Кінетична енергія цього тіла:
 (5)
(5)
Для тіла 5 все аналогічно як і для 4, але вектори відносного і переносного руху будуть мати протилежний напрям, тому вираз для абсолютної швидкості набуде такого вигляду:

Кінетична енергія тіла 5:
 (6)
(6)
Блок 3 здійснює плоскопаралельний рух. Його кінетична енергія дорівнює:

Осьовий
момент інерції
 .
Оскільки кутова швидкість блока 3 та
відносна швидкість тіл 4,5 пов’язані
співвідношенням
.
Оскільки кутова швидкість блока 3 та
відносна швидкість тіл 4,5 пов’язані
співвідношенням
 ,
а отримаємо:
,
а отримаємо:
 ,
(7)
,
(7)
Кінетичну енергію системи, після додавання виразів (2), (3), (5), (6), (7) запишемо:
 (8)
(8)
Знайдемо частинні похідні від кінетичної енергії:






Визначимо
потенціальну енергію системи:
 ,
як роботу сил ваги по переміщенню даних
тіл з поточного положення в початкове.
,
як роботу сил ваги по переміщенню даних
тіл з поточного положення в початкове.
 ,
,




Переміщення
 центра мас тіла 3 визначаеться на підставі
кінематичного співвідношення (4). Запишемо
його у диференціалах і домножимо на dt.
Отримаємо:
центра мас тіла 3 визначаеться на підставі
кінематичного співвідношення (4). Запишемо
його у диференціалах і домножимо на dt.
Отримаємо:

Після
інтегрування цього виразу на проміжку
 отримуємо:
отримуємо:

Звідси при нульових початкових умовах маємо:

Тоді
потенціальна енергія системи, як функція
узагальнених координат
φ,
x
набуває вигляду:

Знаходимо частинні похідні за узагальненими координатами від потенціальної енергії системи:
 ,
,
 (9)
(9)
Узагальнені
сили
 та
та
 визначимо
як коефіцієнти при варіаціях узагальнених
координат у виразі елементарної роботи
непотенціальних сил. До останніх належить
пара сил з моментом M.
визначимо
як коефіцієнти при варіаціях узагальнених
координат у виразі елементарної роботи
непотенціальних сил. До останніх належить
пара сил з моментом M.
Зафіксуємо координату х і надамо механічній системі елементарне переміщення δφ у бік додатних значень зміни кута повороту φ. Відповідна елементарна робота має вигляд:

Звідки маємо

На
елементарному переміщенні
 непотенційні
сили роботи не виконують. Тобто:
непотенційні
сили роботи не виконують. Тобто:
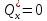
Отже система рівнянь Лагранжа другого роду (1) запишеться так:

(10)

Рівняння (10) можна розв’язати відносно похідних:
 ,
,
 ,
де
,
де

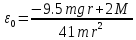
Тоді перші інтеграли диференціальних рівнянь мають вигляд:
 ,
,
 ,
,
А другі інтеграли:


На
підставі початкових умов визначаємо
сталі інтегрування
 і отримуємо шукані рівняння руху
механічної системи:
і отримуємо шукані рівняння руху
механічної системи: