3.2. Составление матрицы смежности

Задача 2. Составить матрицу смежности

3.2.1. Алгоритм составления матрицы смежности

Для полного, непротиворечивого и независимого задания геометрической модели составного тела необходимо использовать матрицу смежности. Это связано с тем, что она обеспечивает возможность организации и воспроизведения процесса моделирования, а также анализа и корректировки модели тела.

Заполнение матрицы смежности осуществляется в порядке формообразования составного геометрического тела и будет, осуществляется в следующей последовательности:

• записывается присвоенный порядковый номер составляющих тел-примитивов порядке возрастания (придерживаются правила; от внешних к внутренним и от больших к меньшим см. ранее);

• записывается наименование составляющих тел-примитивов;

• выявляется число и геометрический смысл параметров формы составляющих тел-примитивов Pф;

• определяется число и геометрический смысл параметров положения составляющих тел Pп;

• выявляется число и геометрический смысл совпадения параметров формы с параметрами формы или положения других составляющих тел-примитивов, рассмотренных перед ними в матрице смежности Кф;

• выявляется число и геометрический смысл совпадения параметров положения с параметрами положения или формы других составляющих тел-примитивов, рассмотренных перед ними в матрице смежности ранее Кп;

• подсчитывается и записывается итоговое число параметров для каждого тела-примитива, а так же обозначение параметров. Например, для тела примитива № 1 запишем: 3 (b1, c1, h1);

• определяется логическая взаимосвязь составляющих тел-примитивов. Для этого используют булевы операции: объединения () и вычитания (/).

Следует помнить, что тела-примитивы, полученные в результате операции вычитания, между собой не взаимодействуют, и соответствующая ячейка матрицы для них не заполняется (пустота не может взаимодействовать с пустотой). Например, считается, что цилиндрическое отверстие 6 не взаимодействует с призматическим отверстием 7, хотя из рисунка видно, что они пересекаются.

Параметры формы и положения (размеры) вытекают непосредственно из задания. Параметры формы Pф тел-примитивов были определены ранее и указаны на эскизах тел примитивов см. рис. 3.

В соответствии с возможными шестью параметрами положения (три переноса и три поворота относительно осей КСК) выявляются параметры положения заданных тел-примитивов Pп относительно КСК заданного составного геометрического тела.

На рис. 4 указаны параметры положения некоторых составляющих тел относительно выбранной системы координат.

Рассмотрим более конкретно некоторые этапы данного алгоритма.

Рис. 4

3.2.2. Заполнение матрицы смежности осуществляется в порядке распознавания, то есть согласно присвоенным номерам тел-примитивов (рис. 4 в Приложении). Например, в рассматриваемом задании призма 1 объединяется с цилиндром 2. Для призмы 1: h1 - высота, c1 - ширина и b1 – длина. У неё отсутствуют параметры положения Рп, так как начало её КСК совпадает началом КСК всего тела. Поскольку призма была принята за базовое тело, то у неё отсутствуют коэффициенты совпадения Кф и Кп. Для цилиндра 2 имеем параметры формы 2 - диаметр и h2 – высота. У него отсутствуют параметры положения Рп, так как начало его КСК совпадает началом КСК всего тела, но поскольку его параметр формы 2 (диаметр) совпадает с параметром базового тела призмы (с её шириной c1), то появляется коэффициент формы Кф, который записывается в соответствующую графу как 2 = c1 и т. д. Так для параллелепипеда (7) параметром положения будет перенос по оси OZ. Для сферы (3) - перенос по оси OZ и т.п.

При определении коэффициентов совпадения и последующей записи их в матицу смежности следует придерживаться правила: Записывается совпадение “текущего” с ”более ранним”. Например, как было отмечено, у цилиндра 2 его диаметр совпадает с шириной призмы 1, записанной ранее. Поэтому во второй строчке матрицы смежности, относящейся к этому цилиндру, в графе Кф записали 2 = c1, т. е. совпадение “текущего” параметра (в данном случае параметра второго тела-примитива) с ”более ранним” параметром (в данном случае с параметром первого тела-примитива). Справедливости ради следует отметить, что если бы мы в первой строчке, относящейся к призме записали в графе Кф зависимость с1 = 2, то во второй строчке (для цилиндра), Кф не надо было указывать и тогда общее количество размеров для простановки осталось бы прежним. Однако в этом случае можно запутаться и несколько раз учесть один и тот же коэффициент. По этому при определении и записи коэффициентов настоятельно рекомендуется придерживаться того правила, что записывается совпадение “текущего” с ”более ранним”.

Матрица смежности выполняется на отдельном формате А4 или А3. Пример заполнения представлен в Приложении (см. рис. 4).

Проверьте, все ли распознанные тела-примитивы включены в матрицу смежности. Убедитесь, что между телами-примитивами полученными операцией “вычитание”, отсутствуют какие-либо взаимосвязи.

3.2.3. Контрольные вопросы

1. Для чего служит операция вычитание? Приведите примеры.

2. Для чего служит операция объединения? Приведите примеры.

3. Какие Вы знаете параметры тел-примитивов? Приведите примеры.

4. В какой последовательности заполняется матрица смежности? Приведите примеры.

5. Какими параметрами в пространстве характеризуются тела-примитивы? Поясните на примере.

6. Какое максимальное количество степеней свободы имеет геометрическое тело в трёхмерном пространстве? Поясните на примере.

7. Что означают Pф и Pп и в каких случаях они появляются? Поясните на примере.

8. Что означают Кф и Кп и в каких случаях они появляются? Поясните на примере.

3.3. Построение трехпроекционного комплексного чертежа отсеков геометрических тел

Задача 3. Построить трехпроекционный комплексный чертеж отсеков геометрических тел в масштабе 1:1.

3.3.1. Алгоритм выполнения построения отсеков

В результате выполнения логических операций (, и /), формируется геометрическое тело как неделимая совокупность тел-примитивов, ограниченная линиями пересечения.

Среди линий пересечения пар геометрических тел-примитивов необходимо выделить линии пересечения, которые не требуют специального построения при формообразовании заданного составного геометрического тела на чертеже. К ним относятся линии, полученные на собирательных изображениях проецирующих поверхностей. Рассмотрим их более подробно. Анализ линий пересечения основан на свойствах пересекающихся тел. В некоторых случаях имеет место использование свойств проецирующих поверхностей. Проецирующими поверхностями называются поверхности, у которых образующие прямые совпадают с направлением проецирующих прямых (лучей). К таким поверхностям относятся поверхности первого порядка (плоскость, призма) и поверхности второго порядка (цилиндры). Эти поверхности могут отображаться как отрезки прямых (плоскости, призмы) или окружность (цилиндр) на ту плоскость проекции, которой перпендикулярны их образующие прямые. Такие проекции поверхностей - прямые и окружности, называются «вырожденными». «Вырожденная» проекция обладает «собирательным» свойством, так как она является областью существования всех точек проецирующей поверхности на плоскости проекций. Линия пересечения поверхностей строится в том случае, если хотя бы одно её изображение не расположено на проецирующей поверхности. Не строят линии пересечения, представляющие из себя окружности, или составные, состоящие из отрезков прямых, если они расположены в плоскости, параллельной одной из плоскостей проекции. В общем случае порядок линии пересечения равен произведению порядков пересекающихся поверхностей.

Проведем анализ линий пересечения заданного геометрического тела и выделим;

а) пересекающиеся пары тел, линии пересечения которых не надо строить:

1. Призма 4 и призма 1;

2. Цилиндр 2 и сфера 3;

3. Цилиндр 2 и призма 1;

4. Цилиндр 2 и цилиндр 6;

б) пересекающиеся пары тел, линии пересечения которых требуют построения только на одной плоскости проекции:

1. Цилиндр 2 и призма 7;

2. Цилиндр 6 и цилиндр 5;

3. Цилиндр 2 и призма 4;

4. Цилиндр 2 и цилиндр 5;

5. Призма 7 и цилиндр 6;

в) пересекающиеся пары тел, линии пересечения которых требуют построения на двух плоскостях проекций:

1. Сфера 3 и призма 7 (результат пересечения – окружности, проецирующиеся в эллипсы).

Поскольку пары поверхностей, отмеченные в пункте а) не требуют специального построения линии пересечения, то её и не строим. Не надо строить линию пересечения для пары пересекающихся поверхностей, если у неё имеется подобная пара. Например, когда имеются две пары пересекающихся, одинаково сориентированных в пространстве поверхностей предположим цилиндров. При этом диаметры цилиндров одной пары отличаются от диаметров другой пары. В рассматриваемом примере это пары 2-5, 6-5 и 7-2, 7-6. Поэтому строим не четыре, а две пары пересекающихся поверхностей. При выборе пары, которую предстоит строить, руководствуются размерами пересекающихся поверхностей. Предпочтение следует отдавать парам с большими линейными размерами, так как линия пересечения в этом случае получается более наглядной и не приходится применять дополнительное масштабирование (увеличение). Для остальных пар отмеченных в пунктах б) и в), построим трехпроекционные комплексные чертежи линий пересечения с использованием «собирательного» свойства «вырожденной» проекции рис. 5.

2 – 5 7 - 2

6 – 5 7 - 6

2 – 4 3 - 7

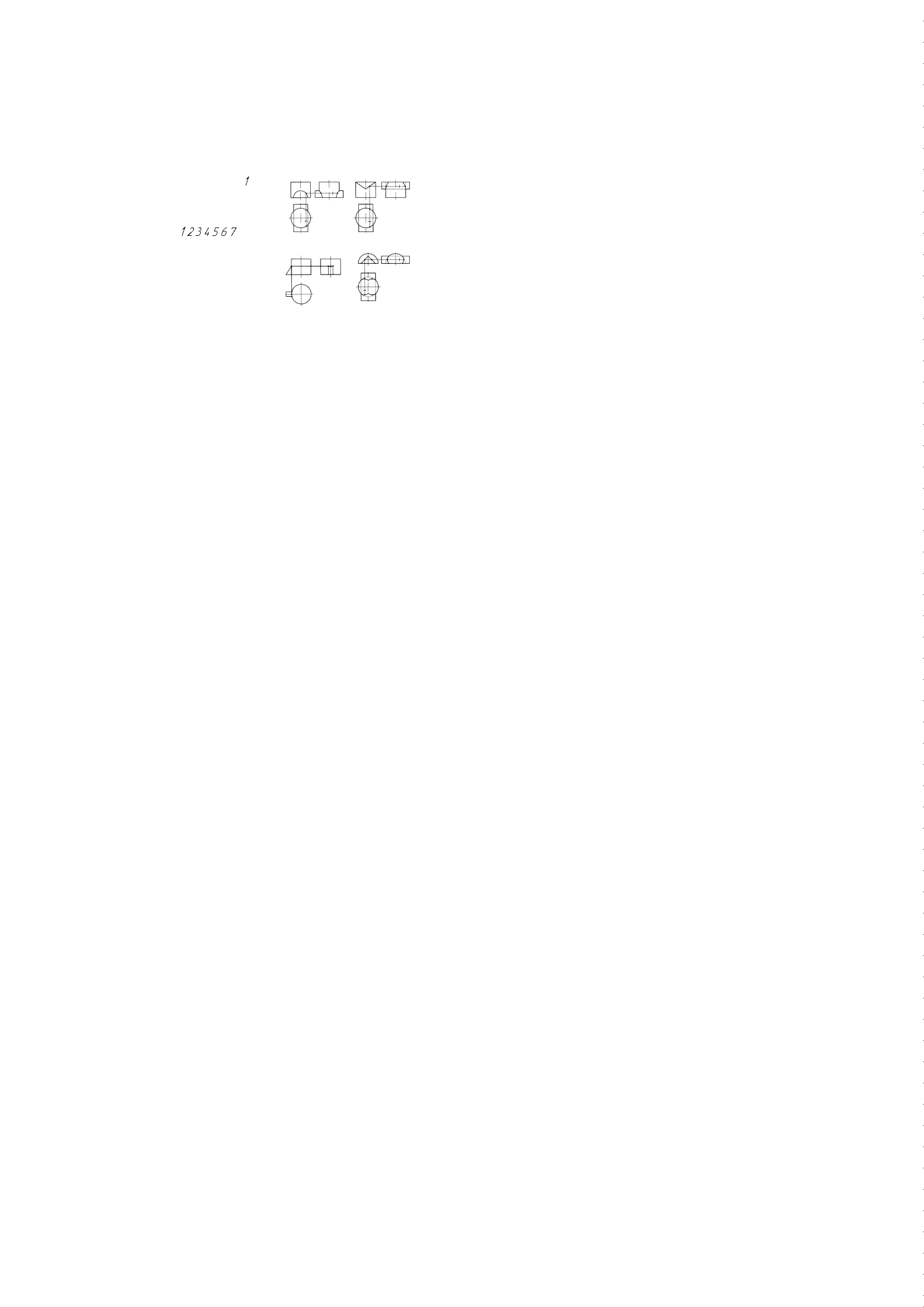
Рис. 5

Применяя булевы операции вычитания (/), получаем отсеки составляющих тел-примитивов рис. 6.

Рис. 6

3.3.2. Построение линии пересечения отсеков поверхностей

Построение начинают с анализа свойств пересекающихся отсеков – их взаиморасположения и положения относительно плоскостей проекций. В соответствии с логикой формообразования и как следствие с логикой простановки размеров строятся составляющие тела-примитивы в порядке распознавания (рис. 5) одновременно на трех проекциях тонкими линиями толщиной S/2 … S/3. Для видимого контура – сплошной линией, а для невидимого - штриховой. Выявляют пары поверхностей ограничивающих тела-примитивы, и строят их линии пересечения последовательно на трех проекциях (см. матрицу смежности). В пояснительной записке описывают все пары пересекающихся поверхностей имеющихся в конкретном варианте. Дают их характеристики и обосновывают необходимость построения на трёхпроекционном комплексном чертеже их линий пересечения. Приводят описание полученных линий пересечения в пространстве и их отображение на чертеже (например, при пересечении пары 3 и 7 получаются окружности, которые на виде сверху и слева отображаются в виде эллипсов). Затем на формате А3 выполняют построение линий пересечения (см. рис. 5 Приложения).

Проверьте, для всех ли пар отмеченных в матрице смежности, построены соответствующие линии пересечения. Если не для всех, то проверьте, нужно ли их строить.

3.3.3. Контрольные вопросы

1. Какие поверхности обладают собирательным свойством? Поясните на примере.

2. Какие поверхности называются проецирующими? Поясните на примере.

3. Как определить порядок линии пересечения поверхностей?

4. В каких случаях линию пересечения следует строить на двух проекциях? Поясните на примере.

3.4. Определение габаритных размеров заданного геометрического тела и компоновка изображений

Задача 4. Определить, габаритные размеры заданного геометрического тела и выполнить компоновку изображений.

3.4.1. Алгоритм выполнения компоновки

Количество изображений в задании определено. Третье изображение (на месте вида слева) выполняется для отработки алгоритма распознавания и построения изображений. Четвертое изображение (вынесенное сечение заданной проецирующей наклонной плоскостью) выполняется для отработки алгоритма определения натуральной величины плоских сечений на основании преобразования комплексного чертежа методом проецирования на новую (дополнительную) плоскость проекции. Для выделения формы внутреннего контура предмета необходимо выполнить на главном изображении сложный фронтальный ступенчатый или ломаный разрез. На изображении слева в задании, как правило, выполняется простой профильный разрез, либо вид слева, совмещенный с простым профильным разрезом.

Компоновка изображений геометрического тела обеспечивает их рациональное размещение на поле формата для нанесения размеров и обозначений рис. 7. Задание выполняется на формате А3 (420 х 297). По габаритным размерам определяют габаритные прямоугольники изображений: для главного изображения - это габаритный прямоугольник со сторонами Н и L, - для вида сверху - L и S, для вида слева - S и Н. Для вынесенного сечения строится габаритный прямоугольник со сторонами N и S, где N - длина секущей плоскости в области геометрического тела. Расположение габаритного прямоугольника вынесенного сечения определяется проекционной связью секущей плоскости и дополнительной плоскости проекции, на которую отображается натуральная величина сечения. Такое положение габаритного прямоугольника является предпочтительным. При построении изображения вынесенного сечения геометрического тела допускается применять также другие преобразования, позволяющие рационально разместить изображение сечения на поле чертежа - это плоскопараллельный перенос и вращение (поворот). В рассматриваемом примере задания выбрано положение, полученное плоскопараллельным переносом и вращением, на что указывается дополнительным знаком рядом с обозначением сечения.

3.4.2. Выполнение компоновки

После определения габаритных размеров прямоугольников необходимо вычислить величины А и В, где А - расстояние от верхней и нижней сторон рамки формата, а В - расстояние от и левой и правой сторон формата и между изображениям. Формулы для вычисления: A = (297-10-H-S)/3 (мм) и В=(425-25-L-S)/3(мм).

Если вынесенное сечение не помещается на поле чертежа, то поскольку оно симметричное, допускается изображать только половину относительно его оси симметрии.

Правильно скомпонованный чертеж должен отвечать следующим основным требованиям:

- равномерное чередование областей изображения и свободных частей поля чертежа

- не допускается «наложение» изображений друг на друга, кроме случаев, предусмотренных стандартами.

Рис. 7

Результатом выполнения компоновки является построение габаритных прямоугольников изображения в масштабе 1:1 (строятся тонкими линиями на формате A3, на котором впоследствии будет выполняться основное изображение, оформленное рамкой и основной надписью).

Проверьте, хватит ли места для нанесения обозначений разрезов и сечений согласно ГОСТ 2.305-68. Хватает ли места для нанесения размеров. Расстояние между размерными линиями и контуром должно быть не менее 10 мм, а между размерными линиями не менее 7 мм. Более подробно о нанесении размеров см. далее. (ГОСТ 2.307-68). Проверьте, не «накладываются» ли изображения друг на друга, или на рамку чертежа. Если нет, то компоновку следует считать законченной.

3.4.3. Контрольные вопросы

1. Каким требованиям должен отвечать правильно скомпонованный чертёж?

2. Какие Вы знаете способы компоновки? Приведите примеры.