Тема 2. Уравнения гиперболического типа . Уравнения малых поперечных колебаний упругой струны.

У нас есть некая гибкая струна, которая колеблется.

В каждый момент времени струна имеет профиль U(x,t) – смещение точки с координатами к моменту времени .

Рассмотрим некоторые ограничения.

, (поперечность). Поперечные колебания реализуются перпендикулярно направлению оси _{и лежат в одной плоскости. В положении равновесия струна лежит на оси х.} Сила внешнего воздействия тоже перпендикулярна направлению оси .

(сила упругости) касательна к профилю струны и ее величина мало меняется со временем _.

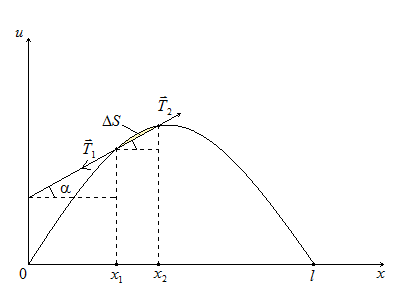
в) Колебания малы, т.е. нет растяжения участков длины (участки практически свою длину не меняют).

_,

.

Длина дуги ∆S:

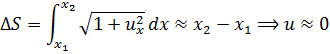, где

.

Условие малости колебаний

_,

Выпишем проекции векторов и на оси.

_.

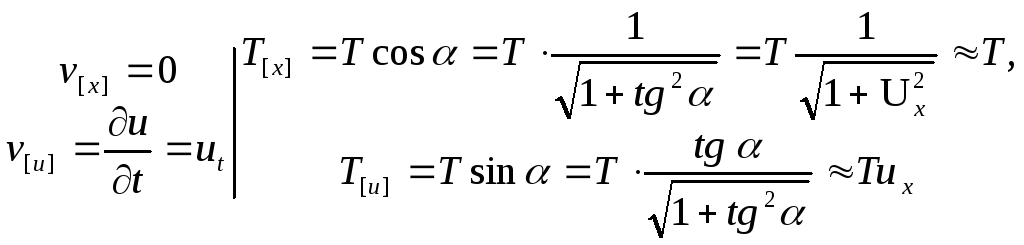Пусть m – массы длины l,

Введем - линейная плотность массы.

Если струна однородна, то . Участок струны dx с dm=kdx, движется со скоростью (x,t).

Для участка dx и ∆x получаем изменение импульса

(x,t)=k(x,t)dx, (t)=(x,t)dx.

Теперь используем 2ой закон Ньютона: ,

_.

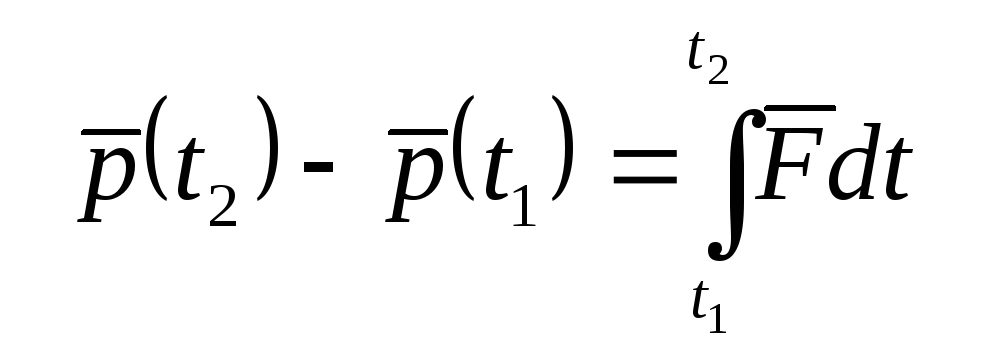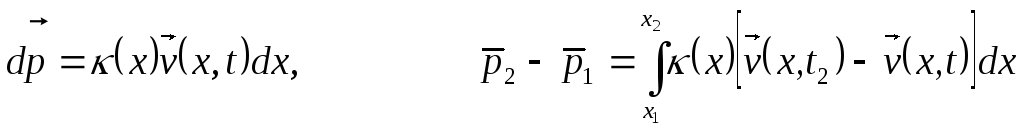Определим силу, силу действующую на участок струны

, где F_вн - внешняя сила.

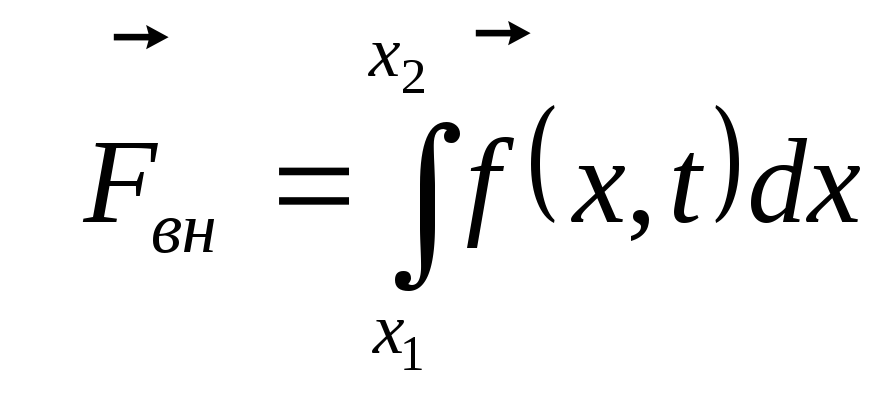Пусть и _. Сила перпендикулярна к оси х, т.е. f_[u]=f , f_[x]=0.

Тогда второй закон Ньютона примет вид векторного равенства

_.

Получаем проекцию векторного равенства на ось Ou:

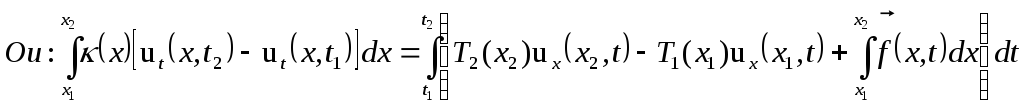
Проекция этого равенства на ось Ох может быть сведена к векторному равенству.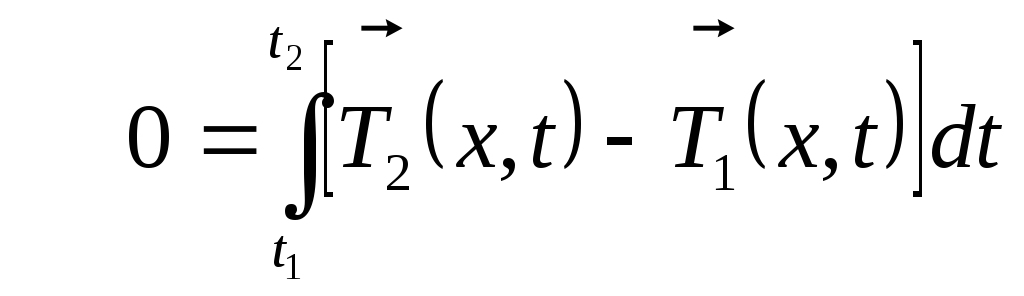

Интеграл не зависит от , и нет зависимости от х. В итоге

_.

_{Получаем:}

=u_x(x₁,t))+ +)dx]dt – интегральное уравнение колебаний струны.

Чтобы привести интегральное уравнение к дифференциальному, нужно воспользоваться теоремой о среднем.

Теорема о среднем

.

Тогда

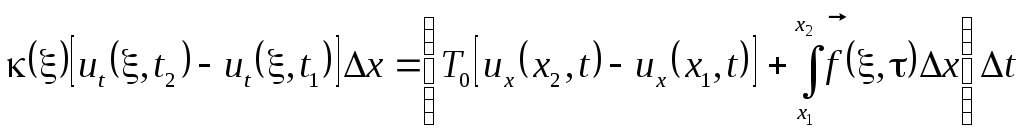_{, где}

_{. После деления на ∆х∆t}

_{и предельного перехода}

_{получаем}

дифференциальное уравнение со вторыми производными

_,

где

_.

Для однородной струны к – постоянна.

(2.1) – уравнение, описывающее малые колебания струны.

Физический смысл v² определим из соображений размерности.

_{, следовательно v является скоростью, не совпадающей со скоростью струны. Ее смысл будет установлен в дальнейшем.}

Покажем, что (2.1) это уравнение гиперболического типа.

В общем виде

_,

Определим дискриминантдля (2.1). Сравнивая с (1.1), получаем

_,

. Следовательно (2.1) является уравнением гиперболического типа.

. Малые продольные колебания упругого стержня

Под действием внешних сил стержень начинает колебаться.

_{Искомая функция} – величина смещения к моменту времени t точки, имевшей в положении равновесия координату х.

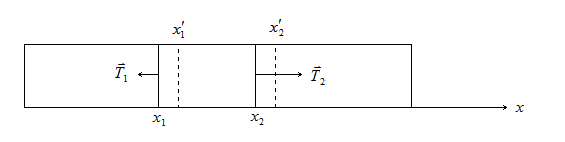
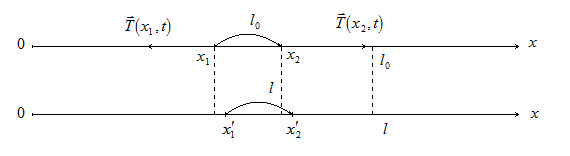
Рассмотрим некоторые ограничения:

колебания точек стержня совершаются вдоль оси , т.е.v=v_x, T=T_x, F=F_x;

работает закон Гука, причем ;

колебания малы (по аналогии с 2.1⁰).

Введем характеристики деформации.

Если длина в положении равновесия,

длина в смещенном положении,

тогда – абсолютное удлинение,

– относительное удлинение.

Пусть

_,

_.

Начало рассматриваемого участка х переходит в _, его конец х+∆х

переходит в _. Тогда

_.

Относительное удлинение примет вид:

_.

Если , получаем:_.

Силу натяжения по закону Гука представим как

.

Будем пользоваться вторым законом Ньютона:

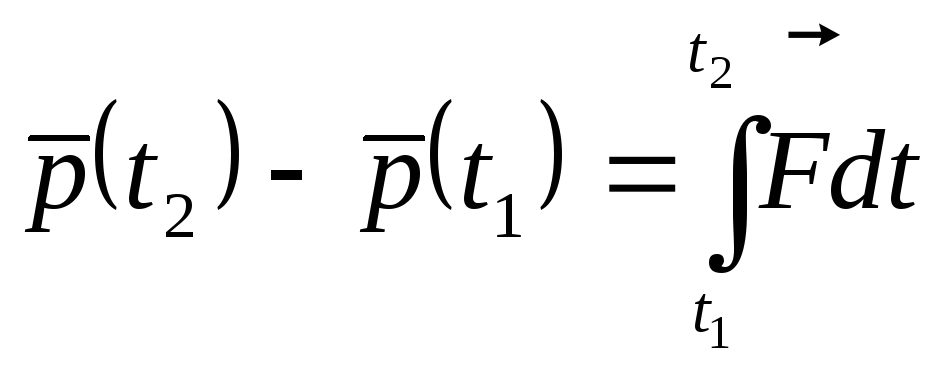_{, где}

.

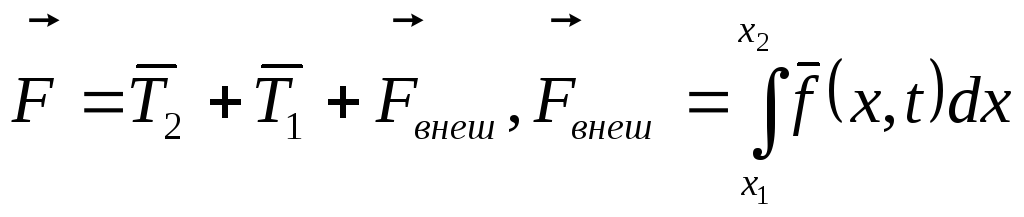Введем линейную плотность массы

dm=kdx, d=(x,t)dm.

_{Если стержень однороден, то. Запишем изменение импульса}

,

.

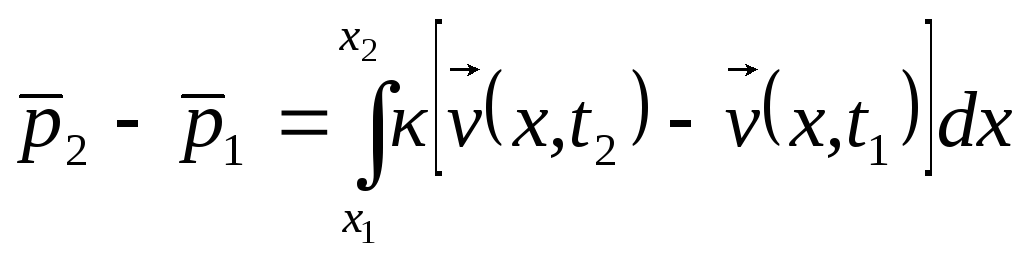В нашем случае .

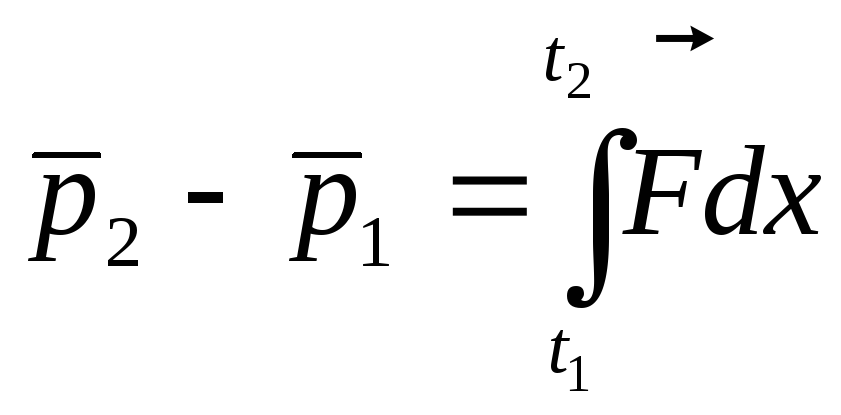Импульс силы равен:

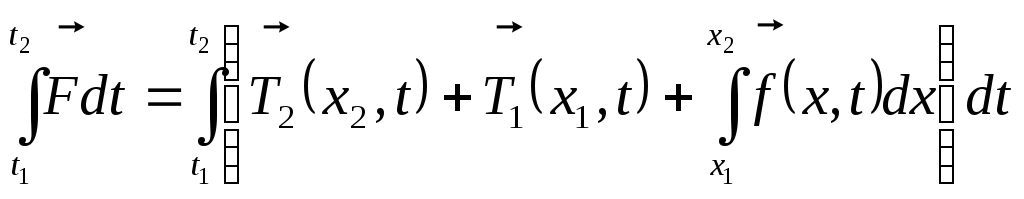_{, тогда по второму закону Ньютона получаем}

_.

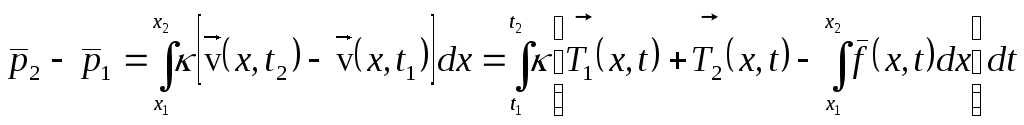Легко видеть, что v_.

Проекция векторного равенства на ось дает

.

Можем воспользоваться теоремой о среднем.

Получаем:

_{Делим на ∆х∆t.}

Устремляем и к нулю и получаем:

_,

_,

_.

Получаем уравнение

_{. (2.2)}

Пусть не зависит от х.

Тогда уравнение (2.2) примет вид

Если ввести: _{, то получим}

– уравнение продольных колебаний стержня, которое совпадает с уравнением для поперечных колебаний струны; т.е. 2 разных математических процесса описываются одинаково.