Асимптоти.

При дослідженні функцій часто буває, що при видаленні координати х точки кривої в нескінченність крива необмежено наближається до деякої прямої.

Визначення. Пряма називається асимптотою кривої, якщо відстань від змінної точки кривої до цієї прямої при видаленні точки в нескінченність прямує до нуля.

Слід зазначити, що не будь-яка крива має асимптоту. Асимптоти можуть бути прямі й похилі. Дослідження функцій на наявність асимптот має велике значення й дозволяє більш точно визначити характер функції й поводження графіка кривої.

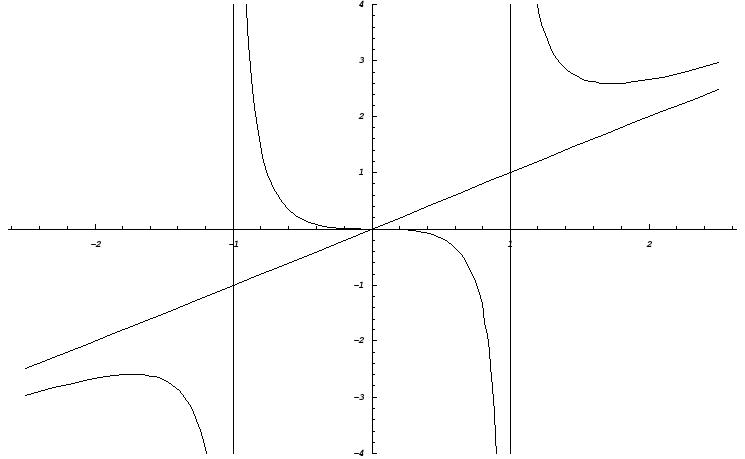
Загалом кажучи, крива, необмежено наближаючись до своєї асимптоти, може й перетинати її, причому не в одній точці, як показано на наведеному нижче графіку функції . Її похила асимптот y = х.

Розглянемо докладніше методи знаходження асимптот кривих.

Вертикальні асимптоти.

З визначення асимптоти треба, що якщо або або , то пряма х = а – асимптота кривої y = f(x).

Наприклад, для функції пряма х = 5 є вертикальною асимптотою.

Похилі асимптоти.

Припустимо, що крива y = f(x) має похилу асимптоту y = kx + b.

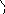
M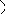



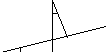
N

 P

Q

Позначимо точку перетину кривої й перпендикуляра до асимптоти – М, Р – точку перетину цього перпендикуляра з асимптотою. Кут між асимптотою і віссю Ох позначимо . Перпендикуляр МQ до осі Ох перетинає асимптоту в точці N.

Тоді MQ = y – ордината точки кривої, NQ = – ордината точки N на асимптоті.

За умовою: , NMP = , .

Кут  – сталий і не рівний 90⁰, тому

Тоді .

Отже, пряма y = kx + b – асимптота кривої. Для точного визначення цієї прямої необхідно знайти спосіб обчислення коефіцієнтів k і b.

В отриманому виразі виносимо за дужки х:

Оскільки х, то , оскільки b = const, то .

Тоді , отже,

.

Оскільки , то , отже,

Відзначимо, що горизонтальні асимптоти є частковим випадком похилих асимптот при k =0.

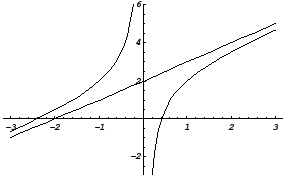
Приклад. Знайти асимптоти й побудувати графік функції .

1) Вертикальні асимптоти: y  + x  0–0; y  – x 0+0, отже, х = 0 – вертикальна асимптота.

2) Похилі асимптоти:

Таким чином, пряма y = х + 2 є похилої асимптотою.

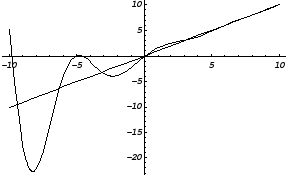
Побудуємо графік функції:

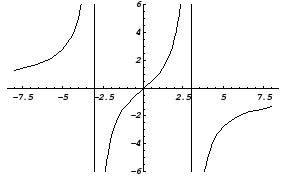
Приклад. Знайти асимптоти й побудувати графік функції .

Прямі х = 3 і х = – 3 є вертикальними асимптотами кривої.

Знайдемо похилі асимптоти:

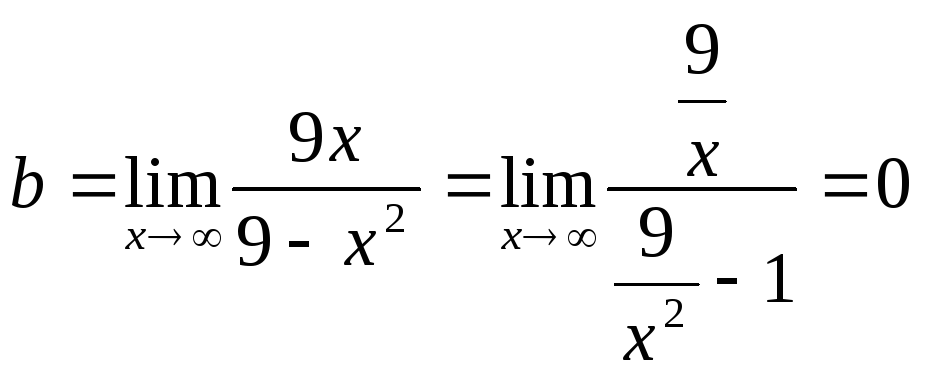
y = 0 – горизонтальна асимптота.

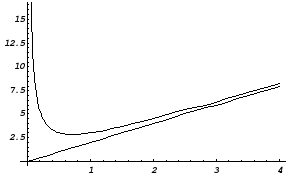
Приклад. Знайти асимптоти й побудувати графік функції .

Пряма х = – 2 є вертикальною асимптотою кривої.

Знайдемо похилі асимптоти.

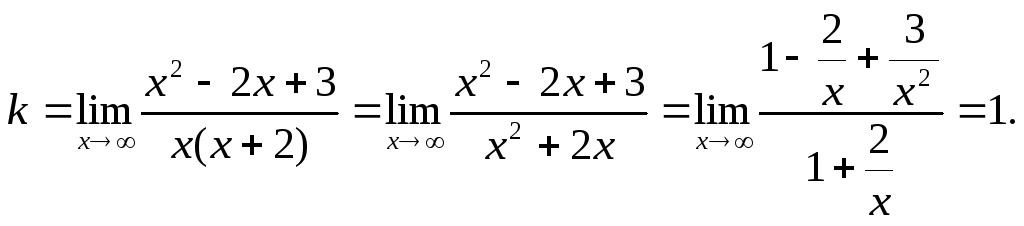
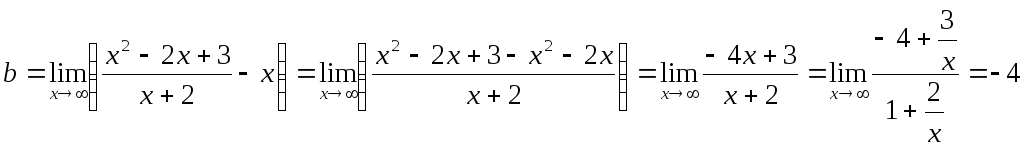
Отже, пряма y = х – 4 є похилою асимптотою.

Схема дослідження функцій

Процес дослідження функції складається з декількох етапів. Для найбільш повного подання про поводження функції й характер її графіка необхідно відшукати:

1. Область існування функції.

Це поняття містить у собі й область значень і область визначення функції.

2. Точки розриву. (Якщо вони є).

3. Інтервали зростання й спадання.

4. Точки максимуму й мінімуму.

5. Максимальне й мінімальне значення функції на її області визначення.

6. Області опуклості й увігнутості.

7. Точки перегину.(Якщо вони є).

8. Асимптоти.(Якщо вони є).

9. Побудова графіка.

Застосування цієї схеми розглянемо на прикладі.

Приклад. Дослідити функцію й побудувати її графік.

Знаходимо область існування функції. Очевидно, що областю визначення функції є область (–; – 1)  (– 1; 1)  (1; ).

У свою чергу, видно, що прямі х = 1, х = – 1 є вертикальними асимптотами кривої.

Областю значень даної функції є інтервал (– ; ).

Точками розриву функції є точки х = 1, х = – 1.

Знаходимо критичні точки.

Знайдемо похідну функції

Критичні точки: x = 0; x = –; x = ; x = – 1; x = 1.

Знайдемо другу похідну функції

.

Визначимо опуклість і увігнутість кривої на проміжках.

–  < x < – , y < 0, крива опукла

– < x < – 1, y < 0, крива опукла

– 1 < x < 0, y > 0, крива увігнута

0 < x < 1, y < 0, крива опукла

1 < x < , y > 0, крива увігнута

< x < , y > 0, крива увігнута

Знаходимо проміжки зростання й спадання функції. Для цього визначаємо знаки похідної функції на проміжках.

–  < x < –, y > 0, функція зростає

– < x < –1, y < 0, функція спадає

–1 < x < 0, y < 0, функція спадає

0 < x < 1, y < 0, функція спадає

1 < x < , y < 0, функція спадає

< x < , y > 0, функція зростає

Видно, що точка х = – є точкою максимуму, а точка х = є точкою мінімуму. Значення функції в цих точках рівні відповідно 3/2 і –3/2.

Про вертикальні асимптоти було вже сказане вище. Тепер знайдемо похилі асимптоти.

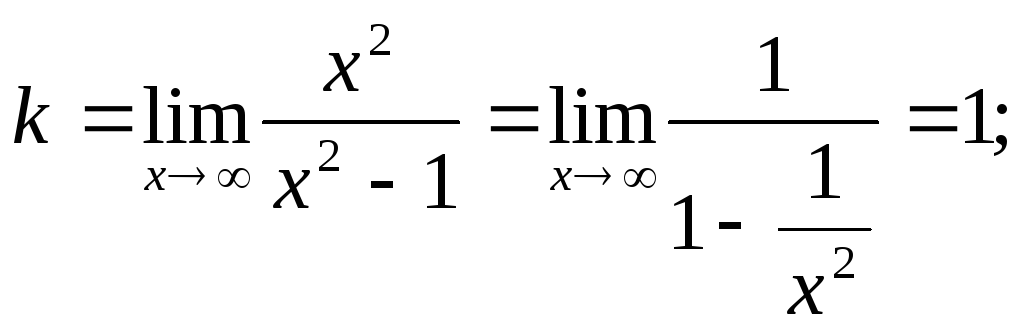
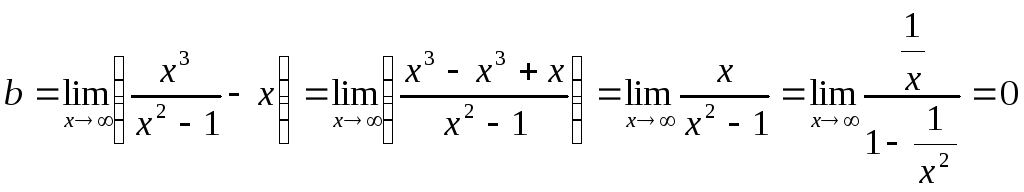
Отже, рівняння похилої асимптоти – y = x.

Побудуємо графік функції: