Об'єм тіл обертання.

Розглянемо криву, задану рівнянням y = f(x). Припустимо, що функція f(x) неперервна на відрізку [a, b]. Якщо відповідну їй криволінійну трапецію з основами а й b обертати навколо осі Ох, то одержимо так зване тіло обертання.

y = f(x)

x

Оскільки кожний перетин тіла площиною x = const являє собою коло радіуса , то об'єм тіла обертання може бути легко знайдений за отриманою вище формулою:

Площа поверхні тіла обертання.

М_i B

А

x

x_i

Визначення: Площею поверхні обертання кривої АВ навколо даної осі називають границю, до якої прямують площі поверхонь обертання ламаних, вписаних у криву АВ, при прямуванні до нуля найбільших з довжин ланок цих ламаних.

Розіб'ємо дугу АВ на n частин точками M₀, M₁, M₂, … , M_n ... Координати вершин отриманої ламаної мають координати x_i і y_i. При обертанні ламаної навколо осі одержимо поверхню, що складається з бічних поверхонь усічених конусів, площа яких дорівнює P_i. Ця площа може бути знайдена за формулою:

Тут S_i – довжина кожної хорди.

Застосовуємо теорему Лагранжа (див. Теорема Лагранжа.) до відношення .

Одержуємо:

Тоді

Площа поверхні, описаної ламаної дорівнює:

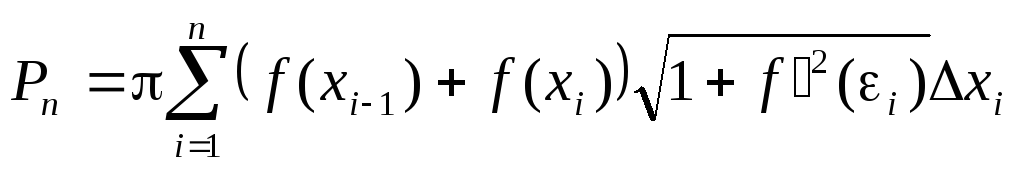
Ця сума не є інтегральної, але можна показати, що

Тоді – формула обчислення площі поверхні тіла обертання.

Функції декількох змінних

При розгляді функцій декількох змінних обмежимося докладним описом функцій двох змінних, тому що всі отримані результати будуть справедливі для функцій довільного числа змінних.

Визначення: Якщо кожній парі незалежних одне від одного чисел (х, у) з деякої множини за якимось правилом ставиться у відповідність одне або кілька значень змінної z, то змінна z називається функцією двох змінних.

z = f(x, y)

Визначення: Якщо парі чисел (х, у) відповідає одне значення z, то функція називається однозначною, а якщо більше одного, то – багатозначною.

Визначення: Областю визначення функції z називається сукупність пар (х, у), при яких функція z існує.

Визначення: Околом точки М₀(х₀, y₀) радіуса r називається сукупність всіх точок (х, у), які задовольняють умові .

Визначення: Число А називається границею функції f (x, y) при прямуванні точки М(х, у) до точки М₀(х₀, y₀), якщо для кожного числа  > 0 знайдеться таке число r > 0, що для будь-якої точки М(х, у), для якої вірна умова

також вірна й умова .

Записують:

Визначення: Нехай точка М₀(х₀, y₀) належить області визначення функції f (x, y). Тоді функція z = f(x, y) називається неперервною в точці М₀(х₀, y₀), якщо

(1)

причому точка М(х, у) прямує до точки М₀(х₀, y₀) довільним чином.

Якщо в будь-якій точці умова (1) не виконується, то ця точка називається точкою розриву функції f (x, y). Це може бути в наступних випадках:

1. Функція z = f(x, y) не визначена в точці М₀(х₀, y₀).

2. Не існує границя .

3. Ця границя існує, але він не дорівнює f (x₀, y₀).

Властивість. Якщо функція f(x, y, ...) визначена й неперервна в замкнутій і обмеженої області D, то в цій області знайдеться принаймні одна точка N(x₀, y₀, …), така, що для інших точок вірна нерівність

а також точка N₁(x₀₁, y₀₁, …), така, що для всіх інших точок вірна нерівність

тоді f (x₀, y₀, …) = M – найбільше значення функції, а f (x₀₁, y₀₁, …) = m – найменше значення функції f (x, y, …) в області D.

Неперервна функція в замкнутій і обмеженій області D досягає принаймні один раз найбільшого значення й один раз найменшого.

Властивість. Якщо функція f (x, y, ...) визначена й неперервна в замкнутій обмеженій області D, а M і m – відповідно найбільше й найменше значення функції в цій області, то для будь-якої точки   [m, M] існує точка N₀(x₀, y₀, …) така, що f (x₀, y₀, …) = .

Простіше кажучи, неперервна функція приймає в області D всі проміжні значення між M і m. Наслідком цієї властивості може служити висновок, що якщо числа M і m різних знаків, то в області D функція принаймні один раз звертається в нуль.

Властивість. Функція f(x, y, …), неперервна в замкнутій обмеженій області D, обмежена в цій області, якщо існує таке число K, що для всіх точок області вірна нерівність .

Властивість. Якщо функція f(x, y, …) визначена й неперервна в замкнутій обмеженій області D, то вона рівномірно неперервна в цій області, тобто для будь-якого позитивного числа  існує таке число  > 0, що для будь-яких двох точок (х₁, y₁) і (х₂, y₂) області, що перебувають на відстані, меншій , виконується нерівність

Наведені вище властивості аналогічні властивостям функцій однієї змінної, неперервним на відрізку. Див. Властивості функцій, неперервних на відрізку.