
- •Диференціальне числення функції однієї змінної. Похідна функції, її геометричний і фізичний зміст.
- •Однобічні похідні функції в точці.
- •Похідна показниково-степеневої функції.
- •Похідна оберненої функцій.
- •Диференціал функції.
- •Формула Тейлора.
- •Формула Маклорена.
- •Подання деяких елементарних функцій за формулою Тейлора.
- •Застосування диференціала до наближених обчислень.
- •Теореми про середнє. Теорема Ролля.
- •Теорема Лагранжа.
- •Теорема Коші.
- •Розкриття невизначеностей. Правило Лопіталя.
- •Точки екстремуму.
- •Дослідження функції на екстремум за допомогою похідних вищих порядків.
- •Опуклість і увігнутість кривої. Точки перегину.
- •Асимптоти.
- •Вертикальні асимптоти.
- •Похилі асимптоти.
- •Векторна функція скалярного аргументу.
- •Властивості похідної векторної функції скалярного аргументу.
- •Параметричне задання функції.
- •Рівняння деяких типів кривих у параметричній формі. Коло.
- •Циклоїда.
- •Астроїда.
- •Похідна функції, заданої параметрично.
- •Кривизна плоскої кривої.
- •Властивості еволюти.
- •Кривизна просторової кривої.
- •Про формули Френе.
- •Інтегральне числення. Первісна функція.
- •Невизначений інтеграл.
- •Методи інтегрування.
- •Безпосереднє інтегрування.
- •Спосіб підстановки (заміни змінних).
- •Інтегрування частинами.
- •Інтегрування елементарних дробів.
- •Інтегрування раціональних функцій. Інтегрування раціональних дробів.
- •Інтегрування деяких тригонометричних функцій.
- •Інтеграл виду .
- •Інтеграл виду , якщо функція r є непарною відносно cos X.
- •Інтегрування деяких ірраціональних функцій.
- •Інтеграл виду де n – натуральне число.
- •Інтегрування біноміальних диференціалів.
- •Інтеграли виду .
- •1 Спосіб. Тригонометрична підстановка.
- •2 Спосіб. Підстановки Ейлера. (1707–1783)
- •3 Спосіб. Метод невизначених коефіцієнтів.
- •Кілька прикладів інтегралів, що не виражаються через елементарні функції.
- •Визначений інтеграл.
- •Властивості визначеного інтеграла.
- •Обчислення визначеного інтеграла.
- •Заміна змінних.
- •Інтегрування частинами.
- •Наближене обчислення визначеного інтеграла.
- •Формула прямокутників.
- •Формула трапецій.
- •Формула парабол
- •Невласні інтеграли.
- •Інтеграл від розривної функції.
- •Геометричні застосування визначеного інтеграла. Обчислення площ плоских фігур.
- •Знаходження площі криволінійного сектора.
- •Обчислення довжини дуги кривої.
- •Обчислення об'ємів тіл. Обчислення об'єму тіла за відомими площами його паралельних перетинів.
- •Об'єм тіл обертання.
- •Площа поверхні тіла обертання.
- •Функції декількох змінних
- •Похідні й диференціали функцій декількох змінних.
- •Повний приріст і повний диференціал.
- •Геометричний зміст повного диференціала. Дотична площина й нормаль до поверхні.
- •Наближені обчислення за допомогою повного диференціала.
- •Частинні похідні вищих порядків.
- •Екстремум функції декількох змінних.
- •Умовний екстремум.
- •Похідна за напрямком.
- •Градієнт.
- •Зв'язок градієнта з похідною за напрямком.
- •Кратні інтеграли.
- •Подвійні інтеграли.
- •Умови існування подвійного інтеграла.
- •Властивості подвійного інтеграла.
- •Обчислення подвійного інтеграла.
- •Заміна змінних у подвійному інтегралі.
- •Подвійний інтеграл у полярних координатах.
- •Потрійний інтеграл.
- •Заміна змінних у потрійному інтегралі.
- •Циліндрична система координат.
- •Сферична система координат.
- •Геометричні й фізичні застосування кратних інтегралів.
Кілька прикладів інтегралів, що не виражаються через елементарні функції.
До
таких інтегралів ставиться інтеграл
виду
![]() ,
де Р(х)
– багаточлен ступеня вище другого. Ці
інтеграли називаються еліптичними.
,
де Р(х)
– багаточлен ступеня вище другого. Ці
інтеграли називаються еліптичними.
Якщо степінь багаточлена Р(х) вище четвертого, то інтеграл називається гіпереліптичним.
Якщо все-таки інтеграл такого виду виражається через елементарні функції, то він називається псевдоеліптичним.
Не можуть бути виражені через елементарні функції наступні інтеграли:
-
 – інтеграл
Пуассона (Сімеон Дені Пуассон –
французький математик (1781–1840))
– інтеграл
Пуассона (Сімеон Дені Пуассон –
французький математик (1781–1840)) -
 – інтеграли Френеля (Жан
Огюстен Френель – французький вчений
(1788–1827) – теорія хвильової оптики та
ін.)
– інтеграли Френеля (Жан
Огюстен Френель – французький вчений
(1788–1827) – теорія хвильової оптики та
ін.) -
 – інтегральний логарифм
– інтегральний логарифм -
 – приводиться до інтегрального
логарифма
– приводиться до інтегрального
логарифма -
 – інтегральний синус
– інтегральний синус -
 – інтегральний косинус
– інтегральний косинус
Визначений інтеграл.
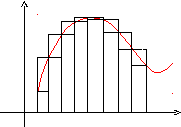
Нехай на відрізку [a, b] задана неперервна функція f(x).
 y
y
M
m
O a xi b x
Позначимо m і M найменше й найбільше значення функції на відрізку [a, b]. Розіб'ємо відрізок [a, b] на частини (необов'язково однакові) n точками.
x0 < x1 < x2 < … < xn
Тоді x1 – x0 = x1, x2 – x1 = x2, … ,xn – xn–1 = xn;
На кожному з отриманих відрізків знайдемо найменше й найбільше значення функції.
[x0, x1] m1, M1; [x1, x2] m2, M2; … [xn–1, xn] mn, Mn...
Складемо суми:
![]() n
= m1x1
+ m2x2
+ … +mnxn
=
n
= m1x1
+ m2x2
+ … +mnxn
=
![]()
![]() n
= M1x1
+ M2x2
+ … + Mnxn
=
n
= M1x1
+ M2x2
+ … + Mnxn
=
![]()
Сума
![]() називається нижньою
інтегральною сумою, а
сума
називається нижньою
інтегральною сумою, а
сума
![]() – верхньою інтегральною
сумою.
– верхньою інтегральною
сумою.
Оскільки
![]() ,
то
,
то
![]() ,
а
,
а
![]() .
.
Усередині кожного відрізка виберемо деяку точку i.
x0 < 1 < x1, x1 < < x2, … , xn–1 < < xn...
Знайдемо значення функції в цих точках і складемо вираз, що називається інтегральною сумою для функції f(x) на відрізку [a, b].
Sn
= f(1)x1
+ f(2)x2
+ … + f(n)xn
=
![]()
Тоді
можна записати:
![]()
Отже,
![]()
![]()
Геометрично це представляється в такий спосіб: графік функції f(x) обмежений зверху описаною ламаною лінією, а знизу – вписаною ламаною.
Позначимо max xi – найбільший відрізок розбивки, а min xi – найменший. Якщо max xi 0, то число відрізків розбивки відрізка [a, b] прямує до нескінченності.
Якщо
![]() ,
то
,
то
![]()
Визначення:
Якщо при будь-яких розбивках відрізка
[a,
b]
таких, що max xi0
і довільному виборі точок i
інтегральна сума
![]() прямує до границі S,
що називається визначеним інтегралом
від f
(x)
на відрізку [a,
b].
прямує до границі S,
що називається визначеним інтегралом
від f
(x)
на відрізку [a,
b].
Позначення
:

а – нижня границя, b – верхня границя, х – змінна інтегрування, [a, b] – відрізок інтегрування.
Визначення:
Якщо для функції f
(x)
існує границя
![]()
 то функція називається інтегрованою
на відрізку [a,
b].
то функція називається інтегрованою
на відрізку [a,
b].
Також
вірні твердження:


Теорема: Якщо функція f(x) неперервна на відрізку [a, b], то вона інтегрована на цьому відрізку.
