
- •Диференціальне числення функції однієї змінної. Похідна функції, її геометричний і фізичний зміст.
- •Однобічні похідні функції в точці.
- •Похідна показниково-степеневої функції.
- •Похідна оберненої функцій.
- •Диференціал функції.
- •Формула Тейлора.
- •Формула Маклорена.
- •Подання деяких елементарних функцій за формулою Тейлора.
- •Застосування диференціала до наближених обчислень.
- •Теореми про середнє. Теорема Ролля.
- •Теорема Лагранжа.
- •Теорема Коші.
- •Розкриття невизначеностей. Правило Лопіталя.
- •Точки екстремуму.
- •Дослідження функції на екстремум за допомогою похідних вищих порядків.
- •Опуклість і увігнутість кривої. Точки перегину.
- •Асимптоти.
- •Вертикальні асимптоти.
- •Похилі асимптоти.
- •Векторна функція скалярного аргументу.
- •Властивості похідної векторної функції скалярного аргументу.
- •Параметричне задання функції.
- •Рівняння деяких типів кривих у параметричній формі. Коло.
- •Циклоїда.
- •Астроїда.
- •Похідна функції, заданої параметрично.
- •Кривизна плоскої кривої.
- •Властивості еволюти.
- •Кривизна просторової кривої.
- •Про формули Френе.
- •Інтегральне числення. Первісна функція.
- •Невизначений інтеграл.
- •Методи інтегрування.
- •Безпосереднє інтегрування.
- •Спосіб підстановки (заміни змінних).
- •Інтегрування частинами.
- •Інтегрування елементарних дробів.
- •Інтегрування раціональних функцій. Інтегрування раціональних дробів.
- •Інтегрування деяких тригонометричних функцій.
- •Інтеграл виду .
- •Інтеграл виду , якщо функція r є непарною відносно cos X.
- •Інтегрування деяких ірраціональних функцій.
- •Інтеграл виду де n – натуральне число.
- •Інтегрування біноміальних диференціалів.
- •Інтеграли виду .
- •1 Спосіб. Тригонометрична підстановка.
- •2 Спосіб. Підстановки Ейлера. (1707–1783)
- •3 Спосіб. Метод невизначених коефіцієнтів.
- •Кілька прикладів інтегралів, що не виражаються через елементарні функції.
- •Визначений інтеграл.
- •Властивості визначеного інтеграла.
- •Обчислення визначеного інтеграла.
- •Заміна змінних.
- •Інтегрування частинами.
- •Наближене обчислення визначеного інтеграла.
- •Формула прямокутників.
- •Формула трапецій.
- •Формула парабол
- •Невласні інтеграли.
- •Інтеграл від розривної функції.
- •Геометричні застосування визначеного інтеграла. Обчислення площ плоских фігур.
- •Знаходження площі криволінійного сектора.
- •Обчислення довжини дуги кривої.
- •Обчислення об'ємів тіл. Обчислення об'єму тіла за відомими площами його паралельних перетинів.
- •Об'єм тіл обертання.
- •Площа поверхні тіла обертання.
- •Функції декількох змінних
- •Похідні й диференціали функцій декількох змінних.
- •Повний приріст і повний диференціал.
- •Геометричний зміст повного диференціала. Дотична площина й нормаль до поверхні.
- •Наближені обчислення за допомогою повного диференціала.
- •Частинні похідні вищих порядків.
- •Екстремум функції декількох змінних.
- •Умовний екстремум.
- •Похідна за напрямком.
- •Градієнт.
- •Зв'язок градієнта з похідною за напрямком.
- •Кратні інтеграли.
- •Подвійні інтеграли.
- •Умови існування подвійного інтеграла.
- •Властивості подвійного інтеграла.
- •Обчислення подвійного інтеграла.
- •Заміна змінних у подвійному інтегралі.
- •Подвійний інтеграл у полярних координатах.
- •Потрійний інтеграл.
- •Заміна змінних у потрійному інтегралі.
- •Циліндрична система координат.
- •Сферична система координат.
- •Геометричні й фізичні застосування кратних інтегралів.
Інтеграл виду , якщо функція r є непарною відносно cos X.
Незважаючи на можливість обчислення такого інтеграла за допомогою універсальної тригонометричної підстановки, раціональніше застосувати підстановку t = sin x.
![]()
Функція
![]() може містити cos
x тільки
в парних ступенях, а отже, може бути
перетворена в раціональну функцію
відносно sin
x.
може містити cos
x тільки
в парних ступенях, а отже, може бути
перетворена в раціональну функцію
відносно sin
x.
![]()
Приклад.

Загалом кажучи, для застосування цього методу необхідна тільки непарність функції щодо косинуса, а ступінь синуса, що входить у функцію може бути кожний, як цілої, так і дробової.
Інтеграл
виду
![]() ,
якщо
,
якщо
функція R є непарною відносно sin x.
За аналогією з розглянутим вище випадком робиться підстановка t = cos x.
Тоді
![]()
Приклад.


Інтеграл
виду
![]()
функція R парна відносно sin x і cos x.
Для перетворення функції R у раціональну використається підстановка t = tgx.
Тоді
![]()
Приклад.
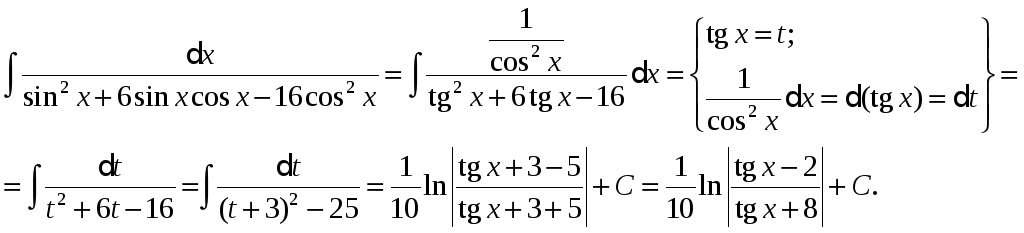
Інтеграл добутку синусів і косинусів
різних аргументів.
Залежно від типу добутку застосуються одна із трьох формул:
![]()
![]()
![]()
Приклад.
![]()
Приклад.

Іноді при інтегруванні тригонометричних функцій зручно використати загальновідомі тригонометричні формули для зниження порядку функцій.
Приклад.
![]()
Приклад.

Іноді застосовуються деякі нестандартні прийоми.
Приклад.

Отже
![]()

Інтегрування деяких ірраціональних функцій.
Далеко не кожна ірраціональна функція може мати інтеграл, виражений елементарними функціями. Для знаходження інтеграла від ірраціональної функції слід застосувати підстановку, що дозволить перетворити функцію в раціональну, інтеграл від якої може бути знайдений як відомо завжди.
Розглянемо деякі прийоми для інтегрування різних типів ірраціональних функцій.
Інтеграл виду де n – натуральне число.
За
допомогою підстановки
![]() функція раціоналізується.
функція раціоналізується.

Тоді

Приклад.


Якщо до складу ірраціональної функції входять коріння різних ступенів, то в якості нової змінної раціонально взяти корінь ступеня, рівного найменшому спільному кратному ступенів корінь, що входять у вираз.
Проілюструємо це на прикладі.
Приклад.
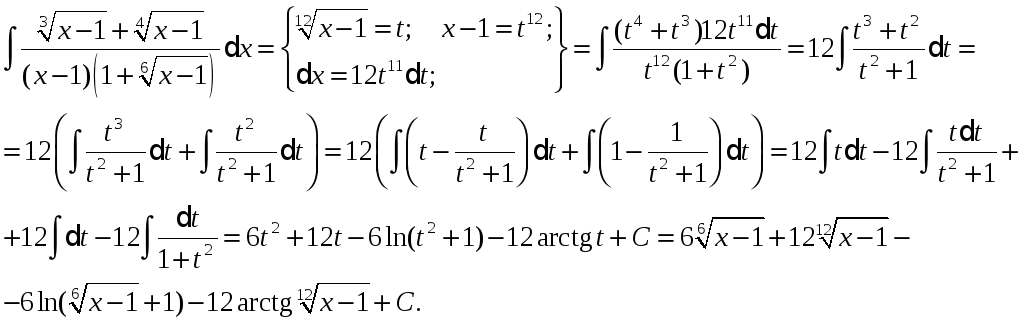
Інтегрування біноміальних диференціалів.
Визначення: Біноміальним диференціалом називається вираз
xm(a + bxn)pdx
де m, n, і p – раціональні числа.
Як було доведено академіком Чебишевим П.Л. (1821–1894), інтеграл від біноміального диференціала може бути виражений через елементарні функції тільки в наступних трьох випадках:
-
Якщо р – ціле число, то інтеграл раціоналізується за допомогою підстановки
![]() ,
де
– спільний знаменник m
і n.
,
де
– спільний знаменник m
і n.
-
Якщо
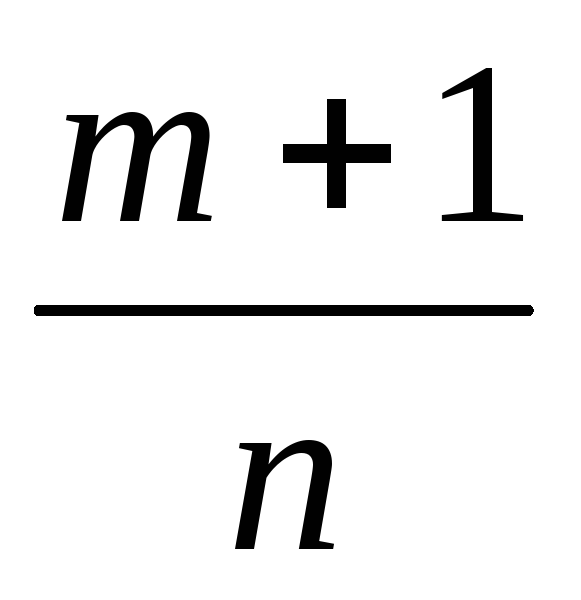 – ціле число, то інтеграл раціоналізується
підстановкою
– ціле число, то інтеграл раціоналізується
підстановкою
 ,
де s
– знаменник числа р.
,
де s
– знаменник числа р.
3)
Якщо
![]() – ціле число, то використовується
підстановка
– ціле число, то використовується
підстановка
![]() ,
де s
– знаменник числа р.
,
де s
– знаменник числа р.
Однак, найбільше практичне значення мають інтеграли від функцій, раціональних щодо аргументу й квадратного кореня із квадратного тричлена.
На розгляді цих інтегралів зупинимося більш докладно.
