Інтегрування раціональних функцій. Інтегрування раціональних дробів.
Для того, щоб проінтегрувати раціональний дріб необхідно розкласти його на елементарні дроби.
Теорема:
Якщо
– правильний раціональний дріб,
знаменник P(x)
якого представлений у вигляді добутку
лінійних і квадратичних множників
(відзначимо, що будь-який багаточлен з
дійсними коефіцієнтами може бути
представлений у такому вигляді: P(x)
= (x
– a)…(x-b)(x2+px+q)…(x2+rx+s)),
то цей дріб може бути розкладена на
елементарні за наступною схемою:
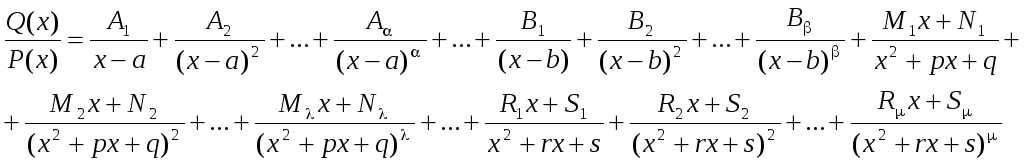
де Ai, Bi, Mi, Ni, Ri, Si – деякі постійні величини.
При інтегруванні раціональних дробів вдаються до розкладу вихідного дробу на елементарні. Для знаходження величин Ai, Bi, Mi, Ni, Ri, Si застосовують так званий метод невизначених коефіцієнтів, суть якого полягає в тому, що для того, щоб два багаточлени були тотожно рівні, необхідно й досить, щоб були рівні коефіцієнти при однакових ступенях х.
Застосування цього методу розглянемо на конкретному прикладі.
Приклад.
Оскільки
,
то
Приводячи до спільного знаменника й дорівнюючи відповідні чисельники, одержуємо:
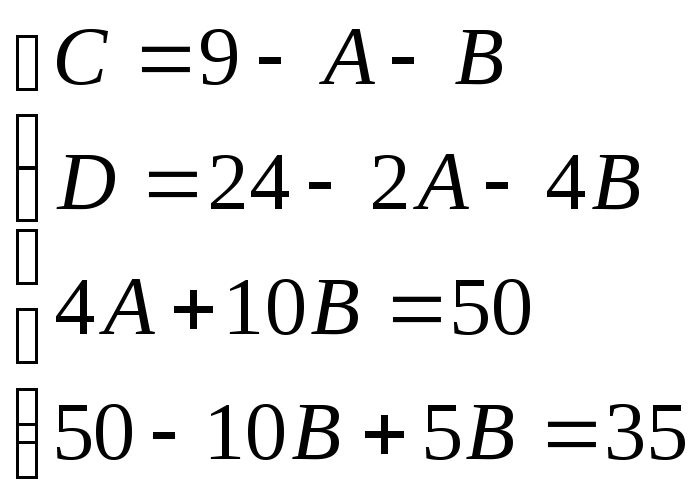
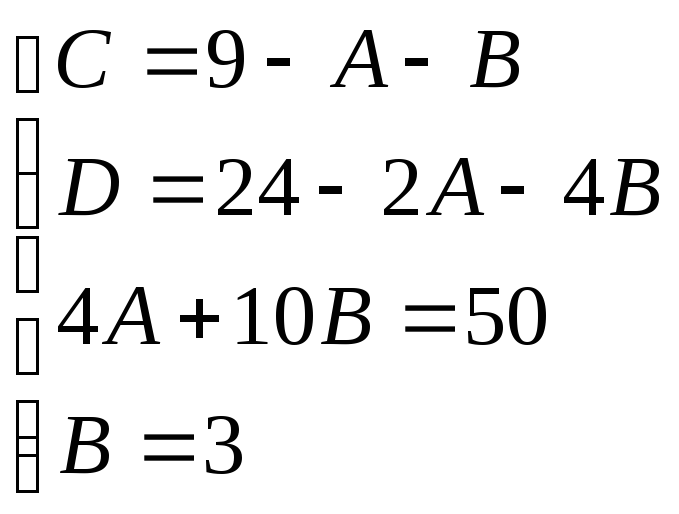
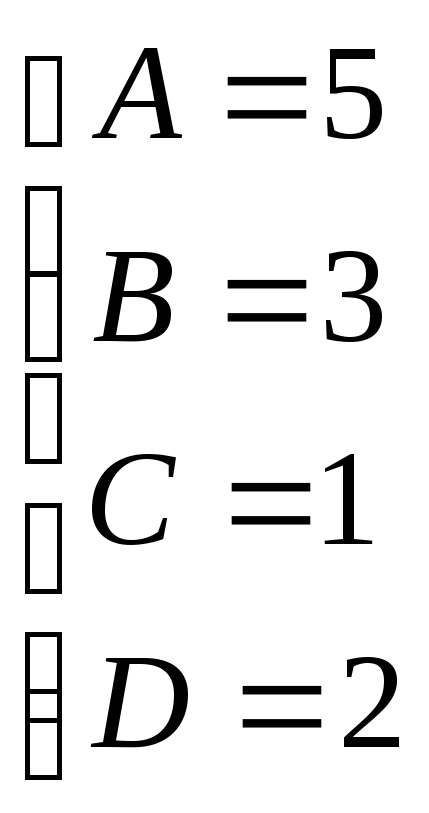
Отже:
Приклад.
Оскільки дріб неправильний, то попередньо слід виділити в ньому цілу частину:
6x5
– 8x4
– 25x3
+ 20x2
– 76x
– 7 3x3
– 4x2
– 17x
+ 6
6x5 – 8x4 – 34x3 + 12x2 2x2 + 3
9x3 + 8x2 – 76x – 7
9x3 – 12x2 – 51x +18
20x2 – 25x – 25
Розкладемо знаменник отриманого дробу на множники. Видно, що при х = 3 знаменник дробу перетворюється в нуль. Тоді:
3x3
– 4x2
– 17x
+ 6 x
– 3
3x3 – 9x2 3x2 + 5x – 2
5x2 – 17x
5x2 – 15x
– 2x + 6
– 2x + 6
0
Таким чином 3x3 – 4x2 – 17x + 6 = (x – 3)(3x2 + 5x – 2) = (x – 3)(x + 2 )(3x – 1). Тоді:
Для того, щоб уникнути при знаходженні невизначених коефіцієнтів розкриття дужок, групування й розв’язання системи рівнянь (яка в деяких випадках може виявитися досить великою) застосовують так званий метод довільних значень. Суть методу полягає в тому, що в отриманий вище вираз підставляються по черзі декілька (по числу невизначених коефіцієнтів) довільних значень х. Для спрощення обчислень прийнято як довільні значення приймати точки, при яких знаменник дробу дорівнює нулю, тобто в нашому випадку – 3, – 2, 1/3. Одержуємо:
Остаточно одержуємо:
=
Приклад.
Знайдемо невизначені коефіцієнти:
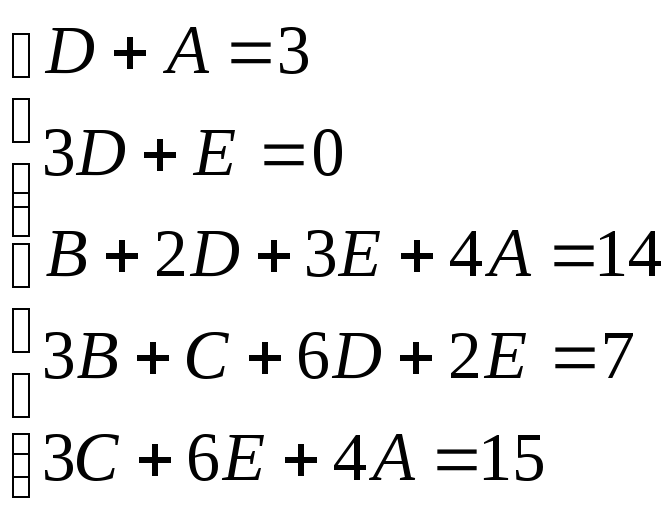
Тоді значення заданого інтеграла:
Інтегрування деяких тригонометричних функцій.
Інтегралів від тригонометричних функцій може бути нескінченно багато. Більшість із цих інтегралів взагалі не можна обчислити аналітично, тому розглянемо деякі найголовніші типи функцій, які можуть бути проінтегровані завжди.
Інтеграл виду .
Тут R – позначення деякої раціональної функції від змінних sin x і cos x.
Інтеграли
цього виду обчислюються за допомогою
підстановки
.
Ця підстановка дозволяє перетворити
тригонометричну функцію в раціональну.
, 
Тоді
У такий
спосіб:
Описане вище перетворення називається універсальною тригонометричною підстановкою.
Приклад.
Безсумнівною перевагою цієї підстановки є те, що з її допомогою завжди можна перетворити тригонометричну функцію в раціональну й обчислити відповідний інтеграл. До недоліків можна віднести те, що при перетворенні може вийти досить складна раціональна функція, інтегрування якої займе багато часу й сил.
Однак при неможливості застосувати раціональнішу заміну змінної цей метод є єдиним результативним.
Приклад.
