Рівняння деяких типів кривих у параметричній формі. Коло.

Якщо центр кола перебуває у початку координат, то координати будь-якої його точки можуть бути знайдені за формулами:

Якщо виключити параметр t, то одержимо канонічне рівняння кола:

x² + y² = r²(cos²t + sin²t) = r²

Еліпс.

Канонічне рівняння: .

у

C M(x, y)

t

О N P

Для довільної точки еліпса М(х, у) з геометричних міркувань можна записати: з ОВР і з OCN, де а – більша піввісь еліпса, а b – менша піввісь еліпса, х і y – координати точки М.

Тоді одержуємо параметричні рівняння еліпса:

де 0  t  2

Кут t називається ексцентричним кутом.

Циклоїда.

y

C

М К

О Р B а 2а х

Визначення. Циклоїдою називається крива, що описує деяка точка, що лежить на кола, коли коло без ковзання котиться по прямій.

Нехай коло радіуса а пересувається без ковзання уздовж осі х. Тоді з геометричних міркувань можна записати: OB = = at; PB = MK = a sin t;

MCB = t; Тоді y = MP = KB = CB – CK = a – a cos t = a(1 – cos t).

x = at – a sin t = a(t – sin t).

Отже: при – це параметричне рівняння циклоїди.

Якщо виключити параметр, то одержуємо:

Як видно, параметричне рівняння циклоїди набагато зручніше у використанні, ніж рівняння, що безпосередньо виражає одну координату через іншу.

Астроїда.

Дана крива являє собою траєкторію точки кола радіуса R/4, що обертається без ковзання по внутрішній стороні кола радіуса R.

R/4

R

Параметричні рівняння, що задають зображену вище криву,

Перетворюючи, одержимо: x^2/3 + y^2/3 = a^2/3 (cos² t + sin² t) = a^2/3

Похідна функції, заданої параметрично.

Нехай .

Припустимо, що ці функції мають похідні й функція x = (t) має зворотну функцію t = Ф(х).

Тоді функція y =  (t) може бути розглянута як складна функція y =  [Ф(х)].

оскільки Ф(х) – обернена функція, то

Остаточно одержуємо:

Таким чином, можна знаходити похідну функції, не знаходячи безпосередньої залежності у від х.

Приклад. Знайти похідну функції

Спосіб 1: Виразимо одну змінну через іншу , тоді

Спосіб 2: Застосуємо параметричне завдання даної кривої: .

x² = a²cos² t;

Кривизна плоскої кривої.

 

В

А А В

Визначення: Кут  повороту дотичної до кривої при переході від точки А до точки В називається кутом суміжності.

Відповідно, вигнутіша та крива, у якої при однаковій довжині більше кут суміжності.

Визначення: Середньою кривизною К_ср дуги називається відношення відповідного кута суміжності  до довжини дуги .

Відзначимо, що для однієї кривої середня кривизна її різних частин може бути різної, тобто дана величина характеризує не криву цілком, а деяка її ділянка.

Визначення: Кривизною дуги в точці К_А називається границя середньої кривизни при прямуванні довжини дуги  0.

Легко бачити, що якщо позначити = ш, то за умови, що кут  – функція, що залежить від S і диференційована, то

Визначення: Радіусом кривизни кривої називається величина .

Нехай крива задана рівнянням y = f(x).

y

B



A  +

x

K_cp = ; ;

Якщо  =  (x) і S = S(x), то .

У той же час .

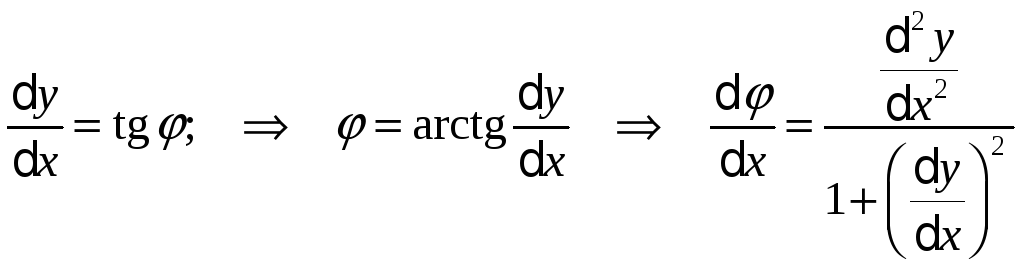Для диференціала дуги: , тоді

Оскільки . В інших позначеннях: .

Розглянемо криву, задану рівнянням: y = f(x).

A

C(a, b)

Якщо побудувати в точці А кривої нормаль, спрямовану убік опуклості, то можна відкласти відрізок АС = R, де R – радіус кривизни кривої у точці А. Тоді точка C(a, b) називається центром кривизни кривої у точці А.

Коло радіуса R із центром у точці C називається колом кривизни.

Очевидно, що в точці А кривизна кривої і кривизна кола рівні.

Можна показати, що координати центра кривизни можуть бути знайдені за формулами:

Визначення: Сукупність всіх центрів кривизни кривої лінії утворять нову лінію, що називається еволютою стосовно даної кривої. Стосовно еволюти вихідна крива називається евольвентою.

Наведені вище рівняння, що визначають координати центрів кривизни кривої визначають рівняння еволюти.