“Курс вищої математики. Частина 2.”

Зміст КВМ Частина 2.

КУРС

ВИЩОЇ

МАТЕМАТИКИ

ЧАСТИНА 2

2005

Диференціальне числення функції однієї змінної. Похідна функції, її геометричний і фізичний зміст.

Визначення. Похідної функції f(x) у точці х = х₀ називається границя відносини приросту функції в цій точці до приросту аргументу, якщо він існує.

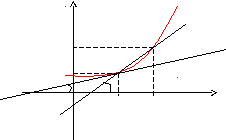у

f(x)

f(x₀ +x) P

f

f(x₀) M

  x

0 x₀ x₀ + x x

Нехай f(x) визначена на деякому проміжку (a, b). Тоді – тангенс кута нахилу січної МР до графіка функції.

,

де  – кут нахилу дотичній до графіка функції f(x) у точці (x₀, f(x₀)).

Кут між кривими може бути визначений як кут між дотичними, проведеними до цих кривих у який-небудь точці.

Рівняння дотичної до кривої:

Рівняння нормалі до кривої: .

Фактично похідна функції показує начебто швидкість зміни функції, як змінюється функція при зміні змінної.

Фізичний зміст похідної функції f(t), де t – час, а f(t) – закон руху (зміни координат) – миттєва швидкість руху.

Відповідно, друга похідна функції – швидкість зміни швидкості, тобто прискорення.

Однобічні похідні функції в точці.

Визначення. Правою (лівою) похідною функції f(x) у точці х = х₀ називається праве (ліве) значення границі відношення за умови, що це відношення існує.

Якщо функція f(x) має похідну в деякій точці х = х₀, то вона має в цій точці однобічні похідні. Однак, зворотне твердження невірне. По-перше функція може мати розрив у точці х₀, а по-друге, навіть якщо функція неперервна в точці х₀, вона може бути в ній не диференційована.

Наприклад: f(x) = x – має в точці х = 0 і ліву й праву похідну, неперервна в цій точці, однак, не має в ній похідної.

Теорема. (Необхідна умова існування похідної) Якщо функція f(x) має похідну в точці х₀, то вона неперервна в цій точці.

Зрозуміло, що ця умова не є достатнім.

Основні правила диференціювання.

Позначимо f(x) = u, g(x) = v – функції, диференційовані в точці х.

1) (u  v) = u  v

2) (uv) = uv + uv

3) , якщо v  0

Ці правила можуть бути легко доведені на основі теорем про границі.

Похідні основних елементарних функцій.

1) С = 0; 9)

2) (x^m) = mx^m–1; 10)

3) 11)

4) 12)

5) 13)

6) 14)

7) 15)

8) 16)

Похідна складної функції.

Теорема. Нехай y = f(x); u = g(x), причому область значень функції u входить в область визначення функції f.

Тоді

Доведення.

(з врахуванням того, що якщо x0, то u0, тому що u = g(x) – неперервна функція)

Тоді

Теорему доведено.

Логарифмічне диференціювання.

Розглянемо функцію .

Тоді (, тому що .

З огляду на отриманий результат, можна записати .

Відношення називається логарифмічною похідною функції f(x).

Спосіб логарифмічного диференціювання полягає в тому, що спочатку знаходять логарифмічну похідну функції, а потім похідну самої функції за формулою

Спосіб логарифмічного диференціювання зручно застосовувати для знаходження похідних складних, особливо показникових функцій, для яких безпосереднє обчислення похідної з використанням правил диференціювання видається трудомістким.