
- •§1. Функция, основные понятия.
- •§2. Основные свойства функций. Четность
- •Периодичность
- •§3. Предел функции. Раскрытие простейших неопределенностей.
- •§4. Сравнение бесконечно малых функций.
- •Говорят, что бесконечно малая a(X) имеет порядок k по сравнению с бесконечно малой b(X) при , если имеют одинаковый порядок малости бесконечно малые a(X) и (b (X))k, то есть
- •Дополнительные упражнения
- •Ответы.
- •§5. Замечательные пределы. Эквивалентные бесконечно малые функции.
- •§6. Односторонние пределы.
- •§7. Непрерывность функции в точке. Точки разрыва.
- •§8. Производная. Правила и формулы дифференцирования.
- •§9. Дифференциал функции, его применение.
- •§10. Дифференцирование неявных и параметрически заданных функций.
- •§11.Геометрический и механический смысл производной.
- •Пример 3
- •Из уравнения первой параболы получаем
- •Дополнительные упражнения
- •§12. Производные высших порядков.
§8. Производная. Правила и формулы дифференцирования.
Приращением функции
![]() называется разность
называется разность
![]() ,
где
,
где
![]() – произвольное малое приращение
аргумента
– произвольное малое приращение
аргумента
![]() .
.
Производной
функции
![]() в
точке
в
точке
![]() называется предел отношения приращения
функции
называется предел отношения приращения
функции
![]() к приращению аргумента
к приращению аргумента
![]() при
при
![]() и обозначается одним из следующих
символов:
и обозначается одним из следующих
символов:
![]()
Таким образом, по определению
![]() или
или ![]() .
.
Если указанный
предел существует, то функцию
![]() называют
дифференцируемой
в точке
называют
дифференцируемой
в точке
![]() ,
а операцию нахождения ее производной
,
а операцию нахождения ее производной
![]() -
дифференцированием.
-
дифференцированием.
Правила дифференцирования.
Если С – постоянная,
![]()
![]() – некоторые дифференцируемые функции,
то:
– некоторые дифференцируемые функции,
то:
-
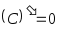 ,
, -

-
 ,
, -

-

-
 в частности,
в частности,
 ,
,

-
если
 ,
т.е.
,
т.е.
 -
сложная функция, составленная из
дифференцируемых функций, то
-
сложная функция, составленная из
дифференцируемых функций, то
![]() .
.
На основании определения производной и правил дифференцирования составляется таблица производных основных элементарных функций:
-
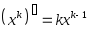 ,
,
 .
. -
 , в
частности
, в
частности  .
. -
 ,
в частности
,
в частности  .
. -
 ;
;
![]() ;
;
![]() ;
;
![]() .
.
5.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
-
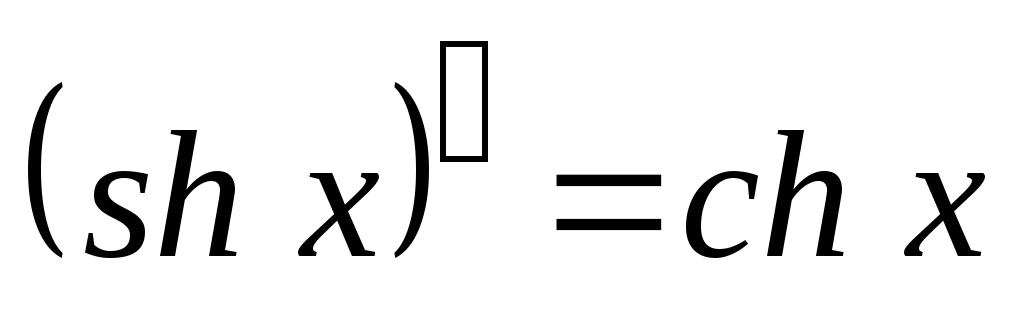 ;
;
![]() ;
;
![]() ,
,
![]() .
.
Пример 1.
Найти производную функции по определению:
а)
![]() ; б)
; б)
![]() .
.
Решение.
а) При любом
приращении
![]() имеем:
имеем:
![]()
![]()
Т.к.
![]() то
то
![]() .
.
б)
![]()
![]()
![]()
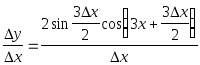
![]()
 .
.
Пример 2.
Доказать, что
функция
![]() в точке
в точке
![]() недифференцируема.
недифференцируема.
Решение.
При любом приращении
![]() найдем приращение функции
найдем приращение функции
![]() в точке
в точке
![]() :
:
![]()
![]()
![]()
Из определения производной следует, что
![]()
![]()
![]()
Так как односторонние
пределы не совпадают, то
![]() не существует. Это и означает, что в
точке
не существует. Это и означает, что в
точке
![]() данная функция не имеет производной,
т.е. недифференцируема .
данная функция не имеет производной,
т.е. недифференцируема .
Пример 3.
Применяя правила и формулы дифференцирования, найти производные следующих функций:
а)
![]() , б)
, б)
![]() ,
,
в)
![]() , г)
, г)![]() ,
,
д)![]() .
.
Решение.
а) Перепишем заданную функцию в виде
![]()
(при этом используются
формулы
![]() и
и
![]() ).
).
Тогда по правилам дифференцирования суммы, вынесения постоянного множителя за знак производной и формуле производной степенной функции получим:
![]()
![]() .
.
б) Преобразуем заданную функцию, раскрыв скобки в числителе и поделив почленно на знаменатель:
![]()
![]()
![]() .
.
в) По правилу дифференцирования произведения и таблице производных находим, что
![]()
![]() .
.
г) По правилу дифференцирования суммы, частного, произведения и таблице производных находим, что
![]()

д) Упростим заданную функцию, пользуясь свойствами логарифмов:
![]()
![]()
![]() .
.
Пример 4.
Применяя правила и формулы дифференцирования, найти производные следующих сложных функций:
а)![]() , б)
, б)![]() , в)
, в)![]() ,
,
г)![]() , д)
, д)![]() ,
,
е)![]() .
.
Решение.
а) Данная функция
является композицией двух функций
![]() и
и
![]() .
По правилу дифференцирования сложной
функции получаем:
.
По правилу дифференцирования сложной
функции получаем:
![]() .
.
б) Данная функция
является композицией трех функций
![]() ,
,
![]() и
и
![]() .
Тогда по правилу дифференцирования
сложной функции получаем:
.
Тогда по правилу дифференцирования
сложной функции получаем:
![]()
![]()
![]() .
.
в)![]()
![]() .
.
г) Сначала применяем правило дифференцирования произведения, а затем - дифференцирования сложной функции:
![]()

д) Сначала применяем правило дифференцирования сложной функции, а затем - дифференцирования частного:
![]()
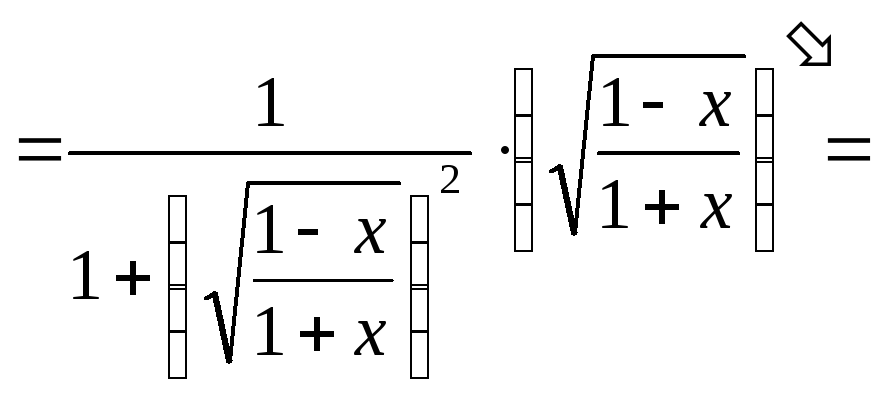

![]()
![]() .
.
е)![]()
![]()
![]()
![]()
![]()
Пример 5.
Найти значение
![]() ,
если
,
если
а)
![]() , б)
, б)![]() .
.
Решение.
а) Упростим функцию, пользуясь свойствами логарифмов
![]()
![]()
![]()
![]() ;
;
при
![]() получим
получим
![]()
б) Найдем производную


![]() .
.
При
![]() получим
получим
![]() .
.
Логарифмической
производной функции
![]() называется
производная от логарифма этой функции,
т.е.
называется
производная от логарифма этой функции,
т.е.
![]() ,
,
откуда находят
![]() .
.
Последовательное
применение логарифмирования и
дифференцирования функций называется
логарифмическим
дифференцированием.
В некоторых случаях оно значительно
упрощает нахождение производной.
Логарифмическое дифференцирование
полезно применять, когда заданная
функция содержит логарифмирующиеся
операции (умножение, деление, возведение
в степень) и, в частности, для нахождения
производной показательно-степенной
функции
![]()
Пример 6.
Используя
логарифмическое дифференцирование,
найти
![]() если
если
а)![]() , б)
, б)![]() ,
,
в)![]() , г)
, г)![]() .
.
Решение.
а) Прологарифмируем функцию:
![]() .
.
Найдем логарифмическую производную
![]()
![]() .
.
Так как
![]() ,
то
,
то
![]() .
.
б) Прологарифмируем функцию:
![]() .
.
Найдем логарифмическую производную
![]()
![]() .
.
Тогда
![]() .
.
в) Прологарифмируем
функцию и продифференцируем по
![]() ,
имея в виду зависимость
,
имея в виду зависимость
![]() от
от
![]() :
:
![]()
![]()
![]()
![]()
В дальнейшем для дифференцирования показательно-степенных функций можно использовать эту формулу.
г) Здесь
![]() .
.
Найдем
![]() ,
,
![]() .
.
Тогда по формуле, выведенной в предыдущем примере, получим
![]()
![]() .
.
Самостоятельная работа.
Вариант 1.
Найти производные функций:
а)
![]() , б)
, б)![]() ,
,
в)![]() , г)
, г)![]() .
.
Вариант 2.
Найти производные функций:
а)![]() , б)
, б)![]() ,
,
в)![]() , г)
, г)![]() .
.
Вариант 3.
Найти производные функций:
а)![]() , б)
, б)![]() ,
,
в)![]() , г)
, г)![]() .
.
Ответы.
Вариант 1. а)![]() , б)
, б)![]() ,
,
в)![]() , г)
, г)![]() .
.
Вариант 2. а)![]() , б)
, б)![]() ,
,
в)![]() , г)
, г)![]() .
.
Вариант 3. а)![]() , б)
, б)
![]() ,
,
в) , г)
, г)
![]() .
.
Дополнительные упражнения.
Найти производные функций:
1)![]() , 2)
, 2)
![]() , 3)
, 3)
![]() ,
,
4)
![]() , 5)
, 5)![]() , 6)
, 6)![]() ,
,
7)![]() , 8)
, 8)![]() .
.
Ответы.
1)![]() ,
,
2)
![]() ,
,
3)![]() ,
,
4)
![]() ,
,
5)![]() ,
,
6)![]()
![]() ,
,
7)![]()
![]() ,
,
8)![]()
![]() .
.
