§4. Сравнение бесконечно малых функций.
Функция
называется бесконечно
малой при
,
если
.
Для сравнения двух
бесконечно малых функций
и
при
находят предел их отношения при
:
-
Если число A = 0 , то говорят, что бесконечно малая a(x) имеет более высокий порядок малости, чем бесконечно малая b(x) при
.
При этом используют
обозначение: a(x)=о(b(x))
при
.
-
Если
,
то говорят, что бесконечно малая a(x)
имеет более
низкий порядок малости, чем
бесконечно
малая b(x)
при
.
При этом очевидно,
что
,
поэтому b(x) = о(a(x)).
-
Если число
,
то говорят, что бесконечно малые a(x)
и b(x)
имеют
одинаковый
порядок малости при
.
При используют
обозначение: a(x)=О(b(x))
при
.
В частности, если
число А = 1,
то бесконечно
малые a(x)
и b(x)
называются
эквивалентными
и обозначаются: 
при
.
4. Если А не существует, то говорят, что бесконечно малые a(x) и b(x) сравнить нельзя.
Говорят, что бесконечно малая a(X) имеет порядок k по сравнению с бесконечно малой b(X) при , если имеют одинаковый порядок малости бесконечно малые a(X) и (b (X))k, то есть
.
Пример 1
Сравнить бесконечно
малые функции a(x)
при
с бесконечно малой функцией b(x) = x,
,
если
1)
2)
3)
4)
Решение.
Вычисляем предел
отношения
в каждом случае:
1)
бесконечно малая
x3
имеет
более высокий порядок малости, чем
бесконечно малая x
при
.
Это означает, что
быстрее, чем
.
Ответ: x3 =
о(x)
при
.
2)
бесконечно малая
имеет
более низкий порядок малости, чем
бесконечно малая x
при
.
Это означает, что
медленнее, чем
.
Ответ: x =
о(
)
при
.
3)
бесконечно малые
10x
и
x
при
имеют
одинаковый порядок малости.
Ответ: 10x =
O(x)
при
.
4) 
следовательно,
есть бесконечно малая, эквивалентная
,
при
.
Ответ:
при
.
Пример2.
Определить порядок
бесконечно малой функции
относительно бесконечно малой
при
.
Решение.
Составим
.
Этот предел будет
равен некоторому числу
,
если сократится
.
Чтобы так произошло, нужно взять k = 8.
Действительно,
.
Таким образом,
k = 8
– это порядок
данной функции y
относительно
функции x
при
.
Ответ:
О(x8),
то есть
k = 8.
Дополнительные упражнения
-
Сравнить бесконечно малые функции a(x) и b(x) при
,
если:
а)
б)
в)
г)
-
Определить порядок относительно x бесконечно малой функции
при
,
если
а)
б)
в)
г)
Ответы.
1.а)
О(b(x)); б)
О(b(x));
в) bn=о(an); г) an=О(bn).
2.а) k = 2; б) k = 0.5;
в) k = 1; г) k = 10.
§5. Замечательные пределы. Эквивалентные бесконечно малые функции.
При раскрытии неопределенностей используются следующие замечательные пределы:
1.
.
-
или
. -
,
в частности
. -
,
в частности
. -
.
Две бесконечно
малые функции a(x)
и b(x)
при
,
если предел их отношения при
равен единице:
при
.
Принцип замены бесконечно малых:
При раскрытии
неопределенностей вида
любой бесконечно малый множитель может
быть заменен на ему эквивалентный.
Теоретические эквивалентности бесконечно малых функций следует из замечательных пределов и записываются следующим образом:
|
1.
|
|
|
2.
|
|
|
3.
|
|
|
4.
|
|
при
при
при
при
при
при
при
Пример 1.
Найти
.
Решение.
Имеем неопределенность
.
Воспользуемся первым замечательным
пределом:
.
Этот же предел можно найти с помощью эквивалентных бесконечно малых:
~
.
Пример 2.
Найти
Решение.
~
~
.
Пример 3.
Найти
.
Решение.
в разности нельзя заменять бесконечно малые функции на им эквивалентные, поэтому сначала проведем преобразования разности в произведение
Пример 4.
Найти
.
Решение.
.
Пример 5.
Найти
Решение.
Разложим числитель на множители, используя формулу разности кубов:
.
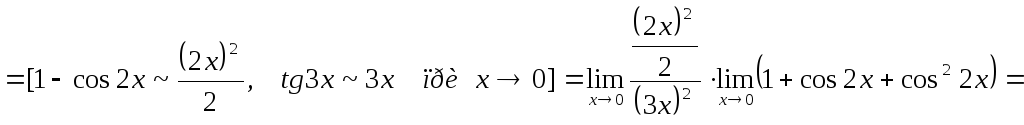
Часто при вычислении пределов бывает удобно сделать замену переменной, чтобы воспользоваться эквивалентными бесконечно малыми функциями.
Пример 5.
Найти
.
Решение.
Получаем
неопределенность
,
но т.к.
,
то сразу воспользоваться эквивалентными
бесконечно малыми нельзя. Введем новую
переменную такую, чтобы она стремилась
к нулю при
:
Пример 6.
Найти
.
Решение.
Имеем неопределенность
,
которую раскрываем с помощью второго
замечательного предела:
,
добившись того, чтобы бесконечно малая
величина z
в основании степени и показатель
были бы взаимно обратными дробями
.
Здесь подразумевалось,
что
при
.
Пример 7.
Найти
.
Решение.
Так как
,
то используем второй замечательный
предел в форме:
.
Для этого в основании выделяем целую
часть дроби:
.
Здесь при
использовании замечательного предела
подразумевали, что
при
.
Пример 8.
Найти
.
Решение.
.
Пример 9.
Найти
.
Решение.
Самостоятельная работа.
Вариант 1.
Найти: а)
; б)
;
в)
; г)
.
Вариант 2.
Найти: а)
; б)
;
в)
; г)
.
Вариант 3.
Найти: а)
; б)
;
в)
; г)
.
Ответы.
Вариант
1: а)
; б)
; в)
; г)
.
Вариант
2: а)
; б)
; в)
; г)
.
Вариант
3: а)
; б)
; в)
; г)
.
Дополнительные упражнения.
-
2.
3.
4.
5.
6.
7.
8.
-
10.
Ответы.
1.
; 2.
; 3.
; 4.
8; 5.
;
6. 24; 7.
; 8.
; 9.
; 10.
.