1.1.2. Ядерные реакции

Ядерными реакциями называются превращения ядер атомов одних химических элементов в ядра других атомов. Ядерные реакции происходят в результате перестройки структуры атомных ядер или же в результате изменения количества нукло­нов в них, при взаимодействии последних между собой и с други­ми частицами (дейтронами, гамма-фотонами, многозарядными ио­нами и т. п.).

В результате взаимодействия ядра с другим ядром или с «бомбардирующей» его частицей происходит изменение состава и строения исходного ядра, вследствие чего в большинстве слу­чаев получается новое ядро (ядро реакции) и обычно еще какая-либо ядерная частица. Следует заметить, что самопроизвольные превращения неустойчивых радиоактивных ядер не относятся к ядерным реакциям в их современном понимании.

Для осуществления ядерных реакций, бомбардирующие ядра и частицы должны обладать большой энергией и большой вероят­ностью столкновения с бомбардируемыми ядрами. Большая энер­гия бомбардирующим частицам необходима для преодоления электростатических сил отталкивания между ними и бомбарди­руемым ядром. Как известно, сила отталкивания F между двумя ядрами может быть определена по формуле Кулона:

F=Z₁Z₂e²/r²

(1.1)

где Z₁ и Z₂ — атомные номера вступающих в реакцию ядер;

е — заряд электрона (е = 4,8- 10^-10 ГСЭ); r — расстояние меж­ду ядрами.

Для того, чтобы началась ядерная реакция, два ядра должны приблизиться друг к другу на расстояние около 10^-15. В этом случае, как следует из формулы (1.1), сила отталкивания весьма велика, особенно у тяжелых ядер. Даже у легких ядер сила отталкивания настолько велика, что для ее преодоления необхо­димо, чтобы энергия ядер была равна миллионам электронвольт. Для протекания же химических реакций, которые являются результатом взаимодействия атомов, их энергия не должна превышать одного электронвольта. Такую энергию значительная часть атомов имеет при температуре 20°С.

Итак, для того, чтобы совершилась ядерная реакция, бомбар­дирующая частица должна проникнуть в ядро-мишень. Только лишь после этого между частицей, протонами и нейтронами ядра-мишени начинают действовать мощные ядерные силы притяжения, благодаря которым и происходит ядерная реакция. При сближении тух ядер на расстояние r необходимо затратить энергию Е, которая выражается формулой

При сближении двух ядер, энергия отталкивания их возрастает и достигает максимального значения Е_макс при их соприкосновении:

(1.2)

где R₁ и R₂— радиусы ядер атомов.

Поскольку радиусы ядер R₁ и R₂ связаны с массовым числом ядер А приближенной зависимостью R = 1,4*10^-13, то зави­симость (1.2) может быть записана в виде

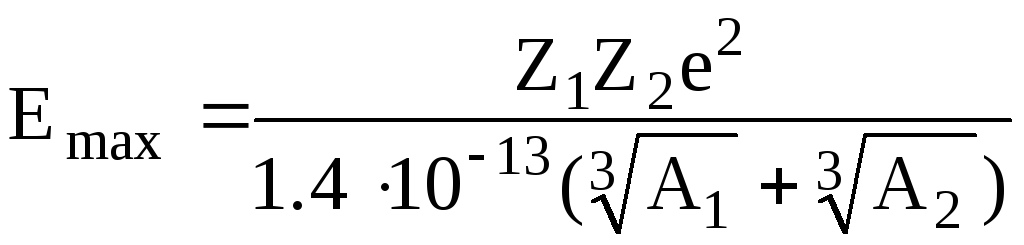(1.3)

Если в формулу (1.3) подставить значение е= 4,8 • 10^-10 CGSE и выразить энергию в МэВ, то формула (1.3) будет выглядеть так:

(1,4)

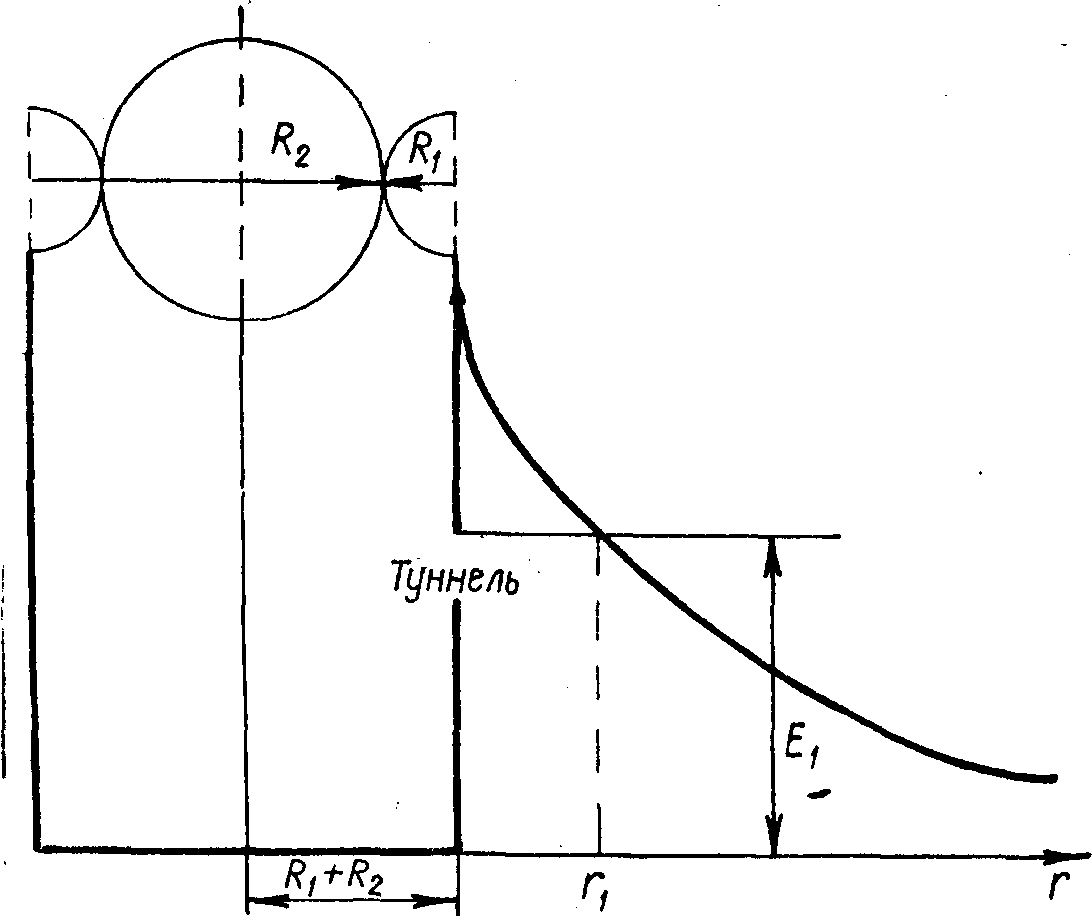
Рис. 1.5. График зависимости энергии электростатического отталкивания от расстояния между ядрами атомов

Следовательно, если энергия Е бомбардирующей частицы больше энергии отталкивания Е_макс, то такая частица свободно проникает в ядро-мишень. Построенная с использованием формулы (1.4) кривая энергии электростатического отталкивания (рис. 1.5) по­казывает, что вокруг ядра-мишени образуется своеобразный по­тенциальный барьер, препятствующий проникновению частиц в яд­ро. Частицы с Е<Емакс, «ударяясь» о потенциальный барьер, как бы отскакивают (отражаются) от него, м вероятность проникнове­ния такой частицы в ядро хотя и существует, но она невелика. Ес­ли частица преодолела расстояние r=R₁+R₂ в этом случае про­исходит резкое падение потенциальной энергии отталкивания. Это объясняется тем, что на указанном и меньших расстояниях дейст­вие ядерных сил во много раз превосходит действие электростати­ческих сил отталкивания. Поэтому на расстояниях r<=R₁+R₂ ядерные силы не только компенсируют отталкивающие электро­статические силы, но и способствуют слиянию ядер под действием сил притяжения. Следовательно, на расстояниях r=R₁+R₂ меж­ду ядрами действуют силы притяжения, которые образуют как бы потенциальную «яму». Эта «яма» имеет приблизительно прямо­угольную форму, так как на всем протяжении ядра действуют одинаковые по величине силы притяжения. Вероятность осущест­вления ядерной реакции определяется двумя условиями:

— энергия бомбардирующей частицы должна обеспечивать преодоление потенциального барьера (E>Eмакс);

— вероятность встречи бомбардирующей частицы с ядром должна быть больше нуля.

Вероятность встречи частицы с ядром-мишенью зависит от вели­чины эффективного сечения ядра (ядерной реакции). Эффектив­ное сечение ядерной реакции  может быть много меньше геомет­рической площади сечения ядра, вследствие действия отталкиваю­щих электростатических сил. За единицу эффективного сечения  ядра принимается один барн, равный 10^-24 см², что соответствует площади сечения ядра. Эффективное сечение ядерных реакций, происходящих в результате действия на ядро-мшшень заряженных частиц даже при энергиях, превышающих высоту кулоновского по­тенциального барьера, обычно в десятки и сотни раз меньше одно­го барна.

В результате взаимодействия заряженных частиц с ядром-ми­шенью, при поглощении последним частицы, ядро оказывается сильно возбужденным и могут произойти различные ядерные реак­ции. Сумма вероятностей всех возможных реакций будет равна ве­роятности проникновения частицы в ядро — полному эффективно­му сечению ядерной реакции _п: _п=_I+_II+_III, где_I,_II,_III- эффективное сечение трех различных типов ядерных реакций, кото­рые описаны ниже.

Следует особо заметить, что имеется класс ядерных реакций, для которых кулоновский потенциальный барьер как бы не су­ществует. Такими реакциями являются реакции с нейтронами. Нейтрон, не имея электрического заряда, не испытывает отталки­вания со стороны ядра и может свободно проникнуть ib ядро и со­вершить ядерную реакцию. Вероятность взаимодействия между ядром и нейтроном возрастает с уменьшением скорости нейтрона. Для медленных (тепловых) нейтронов (с энергией порядка сотых долей электронвольта) эта вероятность гораздо больше, чем для быстрых (с энергией в несколько мегаэлектронвольт). Причиной по­вышенной эффективности тепловых нейтронов при взаимодействии с ядром является то, что дейтрон обладает волновыми свойствами. Нейтрон в явлениях атомного масштаба ведет себя как волна. Нейтрону, как и любой другой движущейся частице с массой т со­путствуют волны де Бройля, длина которых  обратно пропорциональна скорости частицы v, т. е. = h/mv, где h- постоянная Планка.

Чем меньше скорость (а это значит, что меньше и энергия), тем больше длина волны. У быстрых нейтронов с энергией в 1 МэВ длина волны около 10^-14м. У тепловых нейтронов длина волны больше и достигает 1,5*10^-10 м. Длина волны ядерной частицы определяет ее эффективное сечение. Поэтому эффективное сечение медленных (тепловых) нейтронов больше, чем быстрых. Сечения нейтронных реакций для медленных нейтронов могут быть во много раз больше геометрической площади ядра и достигают сотен и даже тысяч барн. Поэтому тепловой нейтрон, размеры которого больше размеров ядра, имеет больше шансов столкнуться с ядром и быть им поглощенным. Проникая в ядро и попадая в сферу действия огромных ядерных сил, нейтрон приходит в очень быстрое движение с чрезвычайно высокой энергией, до 50 МэВ. Такой энергии соответствует очень малая длина волны де Бройля. Размеры нейтрона при такой большой энергии менее одного ферми и он мо­жет свободно размещаться внутри ядра.

Механизм протекания ядерных реакций определяется кинети­ческой энергией бомбардирующих частиц. Если энергия такой час­тицы больше энергии связи нуклона в ядре, то такая частица име­ет возможность вырвать из ядра одну или несколько ядерных частиц. Частица с большой энергией, попадая в ядpo, взаимодействует с одним или же с малым количеством нуклонов. Представляют интерес ядерные реакции, протекающие при энергиях бомбардирующих частиц, значительно меньших энергии связи нуклона в ядре. В этом случае попадающая в ядро частица уже не может вырвать нуклон из ядра. В результате образуется новое ядро с большим числом нуклонов. Такое ядро находится в возбужденном состоянии и называется промежуточным ядром. Энергии промежуточного ядра больше энергии того же ядра в нормальном состоянии. Энергия возбуждения равна сумме кинетической энергии бомбардирующей частицы и ее энергии связи с промежуточным ядром. Для того, чтобы перейти в нормальное устойчивое состоя­ние, такое ядро должно испустить какую-либо частицу (нуклон, группу нуклонов, фотон, гамма-излучение и т. п.), Время сущест­вования промежуточного ядра — время его «жизни» - составляет около 10^-14с. В момент образования промежуточною ядра энергия его возбуждения сосредоточена на захваченной ядром мишенью частице. Затем эта энергия распределяется между частицами ядра по законам случая, т. е. по законам статистики. В результате от­дельный нуклон или группа нуклонов (альфа-частица) в проме­жуточном ядре может приобрести энергию, достаточную для вы­лета из ядра. Вылет частицы приводит к распаду промежуточного ядра. Распад промежуточного ядра не зависит от условий его об­разования, а определяется только свойствами ядра и его энергией возбуждения.

Ядерные реакции обычно записываются в форме уравнений, в левой части которых — символы ядер и частиц, вступающих в реакцию, в правой — получившихся в результате реакции. Правая и левая части уравнения соединяются стрелкой, острие которой об­ращено вправо и указывает на то, что получилось в результате ядерной реакции. В уравнениях ядра записываются обычными символами химических элементов. Вверху символа, слева, пи­шется массовое число ядра, а внизу — атомный номер (за­ряд ядра). Частицы обозначаются следующими символами: альфа-частица (дважды ионизированный атом гелия) — ⁴₂Не (), нейтрон —¹₀n, протон (ядро водорода) —¹₁Н (Р), электрон— ⁰_-1

позитрон —⁰₁, нейтрино — ⁰₀, гамма-квант — и т. д. В обеих частях уравнения любой ядерной реакции суммы атомных и массовых чисел должны быть равны. Например, в результате взаимо­действия нейтрона с ядром бора уравнение ядерной реакции мо­жет быть записано так:

(1,5)

Взаимодействие ядра урана-235 с нейтроном записывается в следующем виде:

(1,6)

В уравнении (1.6) звездочкой обозначено промежуточное (состав­ное) или так называемое возбужденное ядро.

Применяется и сокращенная запись ядерных реакций. Напри­мер, реакцию 1.5 можно записать в виде

Интерпретация этой записи остается прежней: перед скобкой стоит ядро-мишень, в скобках первой обозначена бомбардирую­щая частица, затем — вылетающая частица (их может быть не­сколько) и за скобками — результирующее ядро (ядро от­дачи). Символы частиц в скобках пишутся без массовых и атом­ных чисел.

Наиболее важными ядерными реакциями являются реакции такого типа: упругое рассеяние (n,n), р,р) и т. п.; неупругое рассеяние (n,n), (,); радиационный захват (n,), (р,); ядерный фотоэффект (, n) и (,p); реакция делении ядер тяжелых элементов; реакция синтеза ядер легких элементов.

Тип ядерной реакции определяется бомбардирующий и выле­тающей частицами. Если бомбардирующий и вылетающая частицы одноименны, то протекает реакция (а,а), называемая реакцией рассеяния частицы а. Различают два вида рассеяния. При упругом рассеянии ядро и частица взаимодействуют как два упругих шарика. В этой ядерной реакции внутреннее состояние ядра не изменяется, а между ядром и частицей происходят перераспределение кинетической энергии. Неупругое рассеяние сопровождается возбуждением ядра-мишени без изменения его состава. Часть кинетической энергии неупруго рассеянной частицы тратится на возбуждение ядра. Неупругое рассеяние сапровождается испусканием -квантов возбужденным ядром. В практике упругое и неупругое рассеяние используется для замедления нейтронов. Замедление быстрых нейтронов осуществляется Путем пропускания их через вещества, содержащие легкие ядре (АБ=12): берилий, графит, парафин и т.д.

В реакциях типа (а,в) частица a исчезает поглащается а вместо нее испускается другая частица—в. Состав ядра-мишени изменяется. Реакцию (а,в) называют радиационным захватом частицы а. Поглощение частицы а в радиационном захвате сопровождается испусканием  -квантов.

В реакции ядерного фотоэффекта при поглощении ядром-мишенью -кванта испускается нейтрон или протон.

Энергетически ядерный фотоэффект возможен только при энергиях -кванта, превышающих энергию связи нуклона в ядре. Особенно низок порог фотоэффектов у дейтона и ядра ⁹₄Ве. Дейтон расщепляется на протон и нейтрон -квантами с энергией Е=2,225 МэВ, а в реакции ⁹₄Ве (,n) ⁸₄В пороговая энергия -квантов составляет всего 1,67 МэВ.

В процессе распространения из одной среде в другую часть квантов или частиц меняет свое направление. Для характеристики этого процесса применяется понятие коэффициента рассеяния излучения, или альбедо. Процесс отражения частиц от границы раздела сред наиболее полно характеризуется альбедо по энергии _Е : _Е=Е_ВА/Е_АВ , где Е_ВА,Е_АВ - плотность потоков энергии на границе раздела среды А и среды В.

В ядерных реакциях происходит выделение или поглощение энергии и соответствующей массы. Энергия, выделяющимся и про­цессе ядерных реакций, называется ядерной. Наибольшее выделение ядерной энергии происходит в результате ядерных реак­ций двух типов:

— реакции деления ядер тяжелых элементов (урана, тория, плутония и т. п.);

— реакция синтеза ядер легких элементов (водорода, лития и др.).

Эти реакции используются в ядерных и термоядерных боепри­пасах н будут рассматриваться более подробно.

Реакции деления ядер тяжелых элементов ус­пешно осуществляются при бомбардировке их нейтронами. Нейт­роны электрически нейтральны, не взаимодействуют с электрона­ми оболочек атомов и легко преодолевают электростатические си­лы отталкивания атомных ядер. При взаимодействии нейтронов с ядрами атомов тяжелых элементов (урана и других) во мно­гих случаях происходит мгновенное деление (расщепление) ядра, чаще всего на две части (осколки). Делением атомного ядра на­зывается процесс его распада на два (редко—на три) более лег­ких атомных ядра, называемых осколками деления. Деление свой­ственно атомным ядрам тяжелых радиоактивных элементов, рас­положенных в крице периодической системы элементов Д. И. Мен­делеева (урана, плутония и др.).

В процессе деления ядер имеет место выделение внутриядер­ной энергии в виде кинетической энергии быстролетящих осколков, альфа- и бета-частиц, а также от одного до трех свободных ней­тронов. Свободные (вторичные) нейтроны в свою очередь способ­ны вызвать деление других ядер, вследствие чего число делящих­ся ядер и число нейтронов будет лавинообразно увеличивать­ся. Такая самоподдерживающаяся ядерная реакция называется цепной. Таким образом, один нейтрон дает начало целой цепочке делений. Схема цепной реакции деления ядер урана показана на рис. 1.6.

Теория деления ядер была разработана на основе «капель­ной» модели ядра в СССР Я. И. Френкелем в 1939 году, а позднее — зарубежными учеными Д. Уилером и Бором.

В результате ядерной реакции деления урана выделяется ог­ромное количество энергии. При делении одного ядра урана выде­ляется энергия, равная 195 МэВ, что составляет около одной ты­сячной доли всей внутриядерной энергии этого ядра (2- 10⁵ МэВ).

Примерное распределение энергии (ядерной), выделяющейся при делении одного ядра урана ²³⁵₉₂U:

кинетическая энергия «осколков» .......162МэВ

кинетическая энергия нейтронов ........ 6МэВ

энергия мгновенного -излучения ........6МэВ

энергия радиоактивного излучения «осколков» (бета-, гамма-лучи и нейтрино) .......21МэВ

энергия деления……………………..195МэВ

Высвобождение энергии (около 200 МэВ на одно разделившееся ядро) происходит за счет дефекта массы, который в реакциях де­ления со'ста1вляет 0,1% всей участвовавшей в реакции массы урана. Вещества, в которых возможно осуществление саморазви­вающейся цепной ядерной реакции деления, называют делящими­ся веществами или ядерным горючим. К ним относятся изотопы урана и плутоний-239. Природный уран пред­ставляет собой смесь урна-234 (0,006%), yрана-235 (0,712%) и урана-238 (99,28%). На 140 атомов ypaна-238 прихо­дится всего лишь один атом урана-235. Свойства этих изотопов и отношении деления, вызываемого нейтронами, несколько различны, что объяс­няется тем, что деление ядра урана-235 осуществ­ляется при сообщении ему энергии в 6,5 МэВ, а ядра ypана-238 - при энергии в 7,0 МэВ, Энер­гию, сообщаемую ядру, при которой ядро делит­ся, называют критической энергией деления или энергией активации ядра. Энергии, которую прино­сит ядру нейтрон, называется энергией возбуж­дения. Чем больше ско­рость нейтрона, тем боль­ше энергия возбуждения ядра. В зависимости от скорости нейтроны подразделяются на медленные (тепловые), быстрые, сверхбыстрые и др. (см. 2.5.2).

Важную роль в ядерной энергетике играют медленные или так называемые тепловые нейтроны. Энергия возбуждения, сообщаемая ядру попадающим в него тепловым нейтроном, для урана-235 равна 6,8 МэВ, а для урана-238 — 5,5 MэВ. Это различие объясняется тем, что нейтрон вносит в ядро не только кинетическую энергию (в обоих случаях одинаковую), но и свою энергию связи с ядром, которая для урана-235 равна 6,5 МэВ и 7,0 МэВ для урана-238. Энергия возбуждения тепловых нейтронов ядра урана-235 больше его критической энергии (6,8 против 6,5 МэВ) и значительно меньше для ядра урана-238 (5,5 против 7,0 МэВ). Отсюда следует, что ядра урана-285 могут делиться как быст­рыми, так и тепловыми нейтронами, а урана-238 — только быстрыми и сверхбыстрыми.

Например, реакция деления урана-235 может протекать так:

Механизм делания урана-235 состоит в захвате исходным ядром нейтрона с образованием промежуточного (возбужденного) ядра и с последующим делением последнего через 10^-14—10^-15 с. При этом возможно образование осколков в виде ядер других элементов. У осколков деления энергия связи на один нуклон на 0,9 МэВ боль­ше, чем в ядре урана-235. Следовательно, энергия, освобождаю­щаяся при каждом делении ядра урана, равна Е = Е • А = 0,9 * 235  200 МэВ. Из всех известных реакций деления тяжелых ядер нейтронами наибольший интерес для осуществления ядерно­го взрыва представляет реакция деления ядер атомов урана-233, урана-235 и плутония-239. Указанные изотопы легко делятся ней­тронами небольших энергий (медленными нейтронами). При этом создаются условия для возникновения саморазвивающейся цепной ядерной реакции деления, при которой число делящихся ядер бу­дет нарастать лавинообразно (рис. 1.6) ив течение весьма мало­го промежутка времени выделится огромное количество энергии. Например, при делении всех ядер атомов, находящихся в 1г урана-235 выделяется такое же количество энергии, как при взрыве тротилового заряда массой 20 т. Важнейшей характеристикой цеп­ной ядерной реакции деления является коэффициент развития ре­акции К, который равен отношению среднего числа вторичных ней­тронов, производящих деление ядер, к числу первичных нейтронов, вызвавших деление ядер в данном цикле. При K<1 реакция быст­ро затухает, при K 1 — протекает с постоянной скоростью, при K>1 — реакция саморазвивается, а при К> 1,1 — приобретает взрывной характер. Реакция (цепная) деления ядер атомов, при которой за короткий промежуток времени выделяется ядерная энергия огромной величины, и называется ядерным взрывом. Вре­мя t_к протекания (развития) цепной ядерной реакции деления мо­жет быть определено по формуле

где n_k—общее число ядер, разделившихся при взрыве ядерно­го заряда;— число разделившихся ядер в первом цикле деле­ния; т— период развития реакции — то время, за которое число нейтронов в заряде с K>1 возрастает в е раз; , причем — среднее время жизни нейтронов в заряде из тяжелых ядер. К— коэффициент развития ядерной реакции— эти отношение пол­ного числа нейтронов любого поколения к соответствующему числу нейтронов предыдущего поколения. Коэффициент К всегда меньше среднего числа нейтронов, возникающих при делении одного ядра, так как часть нейтронов теряется в результате:

— внешней утечки из заряда делящегося вещества;

— захвата нейтронов ядрами посторонних примесей в заряде;

— захвата нейтронов ядрами заряда без деления.

Реакция синтеза (соединения) легких ядер яв­ляется способом получения ядерной энергии. Осуществить реакцию синтеза технически существенно сложнее, чем реакцию деления. Соединению ядер препятствуют силы их взаимного электростатического отталкивания. Преодоление этих сил возможно при боль­ших скоростях сближающихся ядер до расстояний, ни которых на­чинают действовать ядерные силы притяжения. Ядерные силы в конечном итоге и обусловливают соединение ядер, сопровождаю­щееся выделением быстрых нейтронов.

Необходимую скорость сближения ядра могут приобрести при нагревании вещества до температуры в несколько десятков мил­лионов градусов. Поэтому реакции синтеза ядер называют термо­ядерными реакциями. В природе условия для термоядерных реак­ций существуют в недрах солнца и звезд. В земных условиях необходимая температура для протекания реакций синтеза ядер пока что достигается только в зоне ядерного взрыва, основанного на делении тяжелых ядер.

Реакция соединения легких ядер таких изотопов, как водород и литий

дейтерий и тритий

в ядра более тяжелых атомов по количеству освобождающейся энергии значительно эффективнее, чем реакция деления. Напри­мер, при синтезе 1 г тритий-дейтериевой смеси (0,4 г дейтерия и 0,6 г трития) освобождается в четыре раза больше энергии, чем при делении 1 г урана.

Взрыв, основанный на синтезе легких ядер - термоядер­ных реакциях, называется термоядерным взрывом.

В зоне ядерных реакций температура и давление достигают огромных величин. Температура Т (в Кельвинах) в зоне ядерной реакции к концу ее развития может быть определена по формуле

(1,7)

где — период развития ядерной реакции, с; q — тротиловый эквивалент заряда, кг; — весовая плотность заряда; — коэф­фициент ислользовадия делящегося вещества.

Так, например, температура в зоне ядерной реакции заряда q = 30 кт ( при =0,2; = 19 г/см³; = 2 • 10^-8с), вычисленная по формуле (1.7), составляет Т35*10⁶ К.

Для приближенной оценки давления р в зоне реакции (р изме­ряется в кгс/см²) можно воспользоваться уравнением кинетической теории газов:

где Т — абсолютная температура газа, которая принимается рав­ной величине температуры, вычисленной по формуле (1.7); k — 1,38 эрг/град — постоянная Больцмана; п — концентрация частиц, 1/см³, определяемая по формуле

(1.8)

где N_A 6,023 • 10²³ — постоянная Авогадро.

При расчете по формуле (1.8) для == 19 г/см³, A = 235 и Z = 92 получим n3,6*10²⁴ частиц/см². Имея значение п, вычис­ленное по формуле (1.8), значение давления в плазме составит р17•10⁹ кг/см². Под действием столь больших давлений вещество заряда стремительно' расширяется, в результате чего цепная реак­ция затухает спустя 2—3 миллионные доли секунды после ее на­чала.