
- •Основные цели и задачи мат физики. Предмет и методы ее исследования.
- •2. Постановка краевой задачи поперечных колебаний тонкой струны.
- •Постановка краевой задачи продольных колебаний стержня.
- •4. Постановка краевой задачи стационарного обтекания тела идеальной жидкостью.
- •5. Постановка краевой задачи переноса тепла в неподвижной среде.
- •6. Классификация краевых задач мат физики. Общая постановка краевых задач мат физики. Понятие корректно и некорректно поставленной задачи.
- •7. Классификация диф ур-й 2 порядка с 2 независимыми переменными.
- •8. Приведение к каноническому виду уравнений гиперболического типа.
- •9. Приведение к каноническому виду уравнений параболического типа.
- •10. Приведение к каноническому виду уравнений эллиптического типа.
- •11. Уравнение Трикоми. Канонический вид ур-я Трикоми.
- •12. Классификация уравнений 2 порядка с числом независимых переменных больше 2.
- •13. Постановка задачи ш-л. Основные свойства собственных значений и собственных функций.
- •14. Основная идея и расчетная схема метода разделения переменных.
- •15. Задача ш-л для отрезка.
- •16. Задача ш-л для отрезка с периодическими граничными условиями.
- •17. Задача Штурма-Лиувиля для прямоугольника и прямоугольного параллелепипеда.
- •18. Задача ш-л для круга.
- •19. Задача ш-л для кругового сектора.
- •20. Задача ш-л для кругового кольца.
- •21. Задача ш-л для цилиндра.
- •22. Задача ш-л для шара.
- •23. Задача ш-л для шарового слоя.
11. Уравнение Трикоми. Канонический вид ур-я Трикоми.
В качестве примера уравнения смешанного типа рассмотрим уравнение Трикоми:

Приведем это уравнение к каноническому виду, а также найдем для него области эллиптичности, гиперболичности и параболичности. Выпишем коэффициенты уравнения:

Тогда
 .
Следовательно, при
.
Следовательно, при
 уравнение (1) является уравнением
эллиптического типа, а при
уравнение (1) является уравнением
эллиптического типа, а при
 – уравнением гиперболического типа.
Область параболичности представляет
собой пустое множество.
– уравнением гиперболического типа.
Область параболичности представляет
собой пустое множество.
Характеристическое уравнение для (1) имеет вид

Тогда


Пусть
 (гиперболическое). Тогда
(гиперболическое). Тогда

Т.о. , характеристиками уравнения Трикоми являются кривые

Выберем в качестве новых переменных:

Дифференцируя:


и подставляя результат в ,
находим:
,
находим:


Подставляя полученные выражения в (1), запишем:

Приводя подобные слагаемые, имеем:

Выразим y через ξ и η.

Тогда имеем:

или, после упрощения,

Уравнение (3) является канонической формой уравнения Трикоми в области гиперболичности.
Пусть
 (эллиптическое). Тогда из характеристического
уравнения следует:
(эллиптическое). Тогда из характеристического
уравнения следует:

Характеристиками уравнения Трикоми в этом случае являются кривые

Выберем в качестве новых переменных

Тогда


Выражения для
 и
и
 принимают вид:
принимают вид:

Подставляя полученные соотношения в (1), имеем:

Произведем необходимые упрощения

и перейдем к новым переменным:
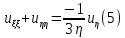
Уравнение (5) есть канонический вид уравнения Трикоми в области эллиптичности.
Уравнение Трикоми представляет интерес для газовой динамики, причем, в области гиперболичности оно соответствует сверхзвуковому движению, а в области эллиптичности – дозвуковому движению.
12. Классификация уравнений 2 порядка с числом независимых переменных больше 2.
Обобщим полученные результаты на линейное Д.У. 2-го порядка со многими независимыми переменными:

Здесь
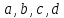 – функции
– функции
 .
Введем новые переменные:
.
Введем новые переменные:

Тогда
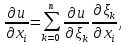

Подставляя полученные выражения (3) в (1), имеем:

Здесь

Рассмотрим квадратичную форму

коэффициенты
которой равны коэффициентам
 исходного уравнения в некоторой точке
исходного уравнения в некоторой точке
 .
Произведем над переменными y
линейное преобразование
.
Произведем над переменными y
линейное преобразование

в результате которого получим новое выражение для квадратичной формы:

Сравнивая (7) и (5), можно убедиться, что коэффициенты уравнения (1) при старшей производной изменяются по тому же закону, что и законы квадратичной формы.
Как известно, матрицу
 квадратичной формы всегда можно привести
к диагональному виду:
квадратичной формы всегда можно привести
к диагональному виду:

Причем

При этом число положительных, отрицательных
и равных нулю коэффициентов
 в каноническом виде квадратичной формы
инвариантно относительно линейного
преобразования.
в каноническом виде квадратичной формы
инвариантно относительно линейного
преобразования.
Назовем уравнение (1) уравнением
эллиптического типа в точке
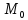 ,
если все n коэффициентов
,
если все n коэффициентов
 имеют один знак; уравнением
гиперболического типа (или нормально
гиперболического типа), если
имеют один знак; уравнением
гиперболического типа (или нормально
гиперболического типа), если
 коэффициентов
коэффициентов
 имеют одинаковый знак, а один коэффициент
– противоположный знак; уравнением
ультрагиперболического типа, если
среди
имеют одинаковый знак, а один коэффициент
– противоположный знак; уравнением
ультрагиперболического типа, если
среди
 имеется m коэффициентов
одного знака и
имеется m коэффициентов
одного знака и
 - противоположного знака (причем,
- противоположного знака (причем,
 и
и
 );
уравнением параболического типа,
если хотя бы один из коэффициентов
);
уравнением параболического типа,
если хотя бы один из коэффициентов
 равен нулю.
равен нулю.
Выбирая независимые переменные
 таким образом, чтобы коэффициенты
преобразования
таким образом, чтобы коэффициенты
преобразования
 в точке
в точке
 приводили квадратичную форму (6) к
каноническому виду, получаем одну из
следующих канонических форм уравнения
(1) в точке
приводили квадратичную форму (6) к
каноническому виду, получаем одну из
следующих канонических форм уравнения
(1) в точке
 :
:




Т.о. если уравнение (1) в некоторой точке M принадлежит к определенному типу, то его можно привести к соответствующему каноническому виду в этой точке.
Для приведения уравнения в некоторой
области к каноническому виду на функции
 следует наложить ограничения вида:
следует наложить ограничения вида:
 .
Число таких условий равно
.
Число таких условий равно
 и при
и при
 превосходит число определяемых функций
превосходит число определяемых функций
 .
Для
.
Для
 недиагональные элементы
недиагональные элементы
 ,
можно обратить в нуль, но диагональные
элементы окажутся при этом различными.
,
можно обратить в нуль, но диагональные
элементы окажутся при этом различными.
Итак при
 уравнение нельзя привести к каноническому
виду в некоторой окрестности точки M.
При
уравнение нельзя привести к каноническому
виду в некоторой окрестности точки M.
При
 можно обратить в нуль единственный
недиагональный коэффициент и выполнить
условие равенства двух диагональных
коэффициентов.
можно обратить в нуль единственный
недиагональный коэффициент и выполнить
условие равенства двух диагональных
коэффициентов.
Если коэффициенты уравнения (1) постоянны, то приводя (1) к каноническому виду в точке M, мы получим уравнение, приведенное к каноническому виду во всей области определения уравнения.
