6. Классификация краевых задач мат физики. Общая постановка краевых задач мат физики. Понятие корректно и некорректно поставленной задачи.

Уравнение вида

или, в более общем случае

описывает процессы колебаний.

Уравнение

или, в более общем случае

описывает процессы теплопередачи и диффузии.

Уравнение или

описывает стационарные процессы. Уравнение (1) относится к уравнениям гиперболического типа, (2) – к уравнениям параболического типа, уравнение (3) – к уравнениям эллиптического типа.

В общем случае эти уравнения имеют бесконечное множество решений. Поэтому в силу единственности на уравнение (3) необходимо наложить граничные условия, а на уравнения (1), (2) – граничные и начальные условия. Рассмотрим область определения уравнений (1) – (3).

Пусть – пространство переменных , – область пространства, занимаемого исследуемой физической системой. Область G является областью определения уравнения (3) в случае стационарных процессов.

В случае нестационарных процессов, описываемых уравнениями (1) и (2), областью определения этих уравнений для систем с твердыми границами является цилиндр, опирающийся на область G, образующие которого направлены вдоль оси времени.

Для систем с подвижными (свободными) границами ситуация усложняется, поскольку с течением времени область G может деформироваться. Как правило, деформация области G описывается отдельными уравнениями, на которые накладываются дополнительные начальные условия.

Под начальными условиями понимают задание состояния физической системы в каждой точке области G в некоторый определенный момент времени .

Под граничными условиями понимают условия на границе области G. Исходя из требования единственности число начальных условий равно порядку дифференцирования по времени, а число граничных условий, равно сумме порядков дифференцирования по координатам.

Вместе начальные и граничные условия образуют краевые условия, а задача решения уравнений с наложенными на него краевыми условиями называется краевой задачей.

Различают следующие основные типы краевых задач.

а) Задача Коши для уравнений гиперболического и параболического типов: задаются начальные условия, область G совпадает со всем пространством , граничные условия отсутствуют.

б) Краевая задача для уравнений эллиптического типа: задаются условия на границе S. Начальные условия отсутствуют.

В общем случае краевая задача для уравнения эллиптического типа состоит в определении функции , удовлетворяющей в области G уравнению (3) и граничному условию на S вида:

Здесь – заданные на S кусочно-непрерывные функции, причем .

Выделяют следующие типы граничных условий:

• граничные условия I-го рода ()

• граничные условия II-го рода ()

• граничные условия III-го рода ()

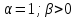Соответствующие краевые задачи называются краевыми задачами I, II, и III рода.

Для уравнения Лапласа и Пуассона краевая задача I рода

называется задачей Дирихле, а краевая задача II рода

– задачей Неймана.

в) Смешанная задача для уравнений гиперболического и параболического типов: область G не совпадает с пространством 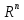, задаются и начальные, и граничные условия.

В большинстве случаев на постановку краевых задач накладываются следующие естественные требования:

• решение должно существовать в некотором классе функций ;

• решение должно быть единственным в некотором классе функций ;

• решение должно непрерывно зависеть от данных задачи (начальных и граничных параметров, свободного члена, коэффициентов уравнения и т.д.).

Задача, удовлетворяющая перечисленным требованиям, называется корректной по Адамару, а множество функций называется классом корректности. Задача, не удовлетворяющая хотя бы одному из перечисленных условий, называется некорректно поставленной. К некорректной постановке часто приводят обратные задачи математической физики.