
- •Основные цели и задачи мат физики. Предмет и методы ее исследования.
- •2. Постановка краевой задачи поперечных колебаний тонкой струны.
- •Постановка краевой задачи продольных колебаний стержня.
- •4. Постановка краевой задачи стационарного обтекания тела идеальной жидкостью.
- •5. Постановка краевой задачи переноса тепла в неподвижной среде.
- •6. Классификация краевых задач мат физики. Общая постановка краевых задач мат физики. Понятие корректно и некорректно поставленной задачи.
- •7. Классификация диф ур-й 2 порядка с 2 независимыми переменными.
- •8. Приведение к каноническому виду уравнений гиперболического типа.
- •9. Приведение к каноническому виду уравнений параболического типа.
- •10. Приведение к каноническому виду уравнений эллиптического типа.
- •11. Уравнение Трикоми. Канонический вид ур-я Трикоми.
- •12. Классификация уравнений 2 порядка с числом независимых переменных больше 2.
- •13. Постановка задачи ш-л. Основные свойства собственных значений и собственных функций.
- •14. Основная идея и расчетная схема метода разделения переменных.
- •15. Задача ш-л для отрезка.
- •16. Задача ш-л для отрезка с периодическими граничными условиями.
- •17. Задача Штурма-Лиувиля для прямоугольника и прямоугольного параллелепипеда.
- •18. Задача ш-л для круга.
- •19. Задача ш-л для кругового сектора.
- •20. Задача ш-л для кругового кольца.
- •21. Задача ш-л для цилиндра.
- •22. Задача ш-л для шара.
- •23. Задача ш-л для шарового слоя.
18. Задача ш-л для круга.
Найти
решения уравнения

с граничным условием

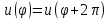
Введем
полярную систему координат
 .
Раскрывая лапласиан, запишем
.
Раскрывая лапласиан, запишем


Подставляя
(4) в () и поделив обе части полученного
уравнения на
 ,
получим:
,
получим:

Уравнение (5) эквивалентно системе обыкновенных Д.У.:


Подставляя (4) в граничное условие (2), и сокращая Φ, имеем

Т.о, задачу (1) – (2) можно представить в
виде двух задач для
 и
и
 :
:


Начнем решение с задачи (9), представляющей
задачу Ш-Л для отрезка с периодическими
граничными условиями. Соб знач этой
задачи равны:
 а
собственные функции –
а
собственные функции –

Перейдем к решению задачи (8) с учетом
значения
 ;
выполняя замену
;
выполняя замену
 и выполняя преобразования, имеем:
и выполняя преобразования, имеем:

Уравнение (12) представляет собой уравнение Бесселя. Его общее решение имеет вид:

Тогда

При
 функция Неймана
функция Неймана
 обращается в бесконечность. По этой
причине потребуем равенства нулю
коэффициента
обращается в бесконечность. По этой
причине потребуем равенства нулю
коэффициента
 :
:

Для
определения собственных значений
 подставим функцию (14) в граничное
условие системы (8). Имеем:
подставим функцию (14) в граничное
условие системы (8). Имеем:

Полученное
выражение представляет собой
трансцендентное уравнение относительно
λ. Пусть соб знач имеют вид
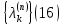 Тогда
соб ф имеют вид:
Тогда
соб ф имеют вид:
 .
.
Подставляя полученный результат имеем
соб ф :

19. Задача ш-л для кругового сектора.
Пусть D – круговой
сектор:
 ,
,
 ;
C – граница области
D.
;
C – граница области
D.
Задача Ш-Л имеет вид:
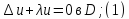





Представляя функцию u в виде произведения

и
разделяя переменные, получим две краевые
задачи относительно переменных r
и
 :
:

Вторая краевая задача представляет
задачу Ш-Л для отрезка. Ее общее решение
имеет вид:


Решением (6) являются собственные значения
 .
Собственные функции задачи Штурма-Лиувилля
для отрезка имеют вид:
.
Собственные функции задачи Штурма-Лиувилля
для отрезка имеют вид:

По
аналогии с задачей для круга, запишем
радиальную функцию
 :
:

Подставим (8) в (6) для R:

(9) – уравнение для нахождения с.з.
 (10). Подставим (8) и (7) в (3), получим
с.ф.
(10). Подставим (8) и (7) в (3), получим
с.ф.

20. Задача ш-л для кругового кольца.
Пусть
D – круговое кольцо,
 ,
,
 .
.

Задача Ш-Л для этой системы имеет вид:


Представляя искомое решение в виде
произведения

и
разделяя переменные в (1) – (2), получим
две краевые задачи для радиальной
 и угловой
и угловой
 функций:
функций:

Вторая
краевая задача полностью совпадает с
задачей для круга. Ее собственные
значения равны
 ,
а собственные функции имеют вид:
,
а собственные функции имеют вид: 
Решение
уравнения для
 в первой краевой задаче имеет вид:
в первой краевой задаче имеет вид:

Поскольку точка с
 не входит в рассматриваемую область D,
равенства нулю коэффициента при функции
Неймана не требуется. Подставим полученный
результат в граничные условия и запишем
следующую систему:
не входит в рассматриваемую область D,
равенства нулю коэффициента при функции
Неймана не требуется. Подставим полученный
результат в граничные условия и запишем
следующую систему:

Потребуем
равенства нулю определителя, составленного
из коэффициентов при
 и
и
 :
:

Последнее
выражение представляет собой
трансцендентное уравнение относительно
 .
Обозначим его корни через
.
Обозначим его корни через
 .
Итак, семейство
.
Итак, семейство
 образует
спектр собственных значений задачи Ш-Л
для кругового кольца. Для определения
собственных функций найдем связь между
коэффициентами
образует
спектр собственных значений задачи Ш-Л
для кругового кольца. Для определения
собственных функций найдем связь между
коэффициентами
 и
и
 .
Из определителя видно:
.
Из определителя видно:


Тогда радиальная функция
 имеет вид:
имеет вид:

И окончательно получаем следующий вид собственных функций задачи Ш-Л для кругового кольца:

