
- •Основные цели и задачи мат физики. Предмет и методы ее исследования.
- •2. Постановка краевой задачи поперечных колебаний тонкой струны.
- •Постановка краевой задачи продольных колебаний стержня.
- •4. Постановка краевой задачи стационарного обтекания тела идеальной жидкостью.
- •5. Постановка краевой задачи переноса тепла в неподвижной среде.
- •6. Классификация краевых задач мат физики. Общая постановка краевых задач мат физики. Понятие корректно и некорректно поставленной задачи.
- •7. Классификация диф ур-й 2 порядка с 2 независимыми переменными.
- •8. Приведение к каноническому виду уравнений гиперболического типа.
- •9. Приведение к каноническому виду уравнений параболического типа.
- •10. Приведение к каноническому виду уравнений эллиптического типа.
- •11. Уравнение Трикоми. Канонический вид ур-я Трикоми.
- •12. Классификация уравнений 2 порядка с числом независимых переменных больше 2.
- •13. Постановка задачи ш-л. Основные свойства собственных значений и собственных функций.
- •14. Основная идея и расчетная схема метода разделения переменных.
- •15. Задача ш-л для отрезка.
- •16. Задача ш-л для отрезка с периодическими граничными условиями.
- •17. Задача Штурма-Лиувиля для прямоугольника и прямоугольного параллелепипеда.
- •18. Задача ш-л для круга.
- •19. Задача ш-л для кругового сектора.
- •20. Задача ш-л для кругового кольца.
- •21. Задача ш-л для цилиндра.
- •22. Задача ш-л для шара.
- •23. Задача ш-л для шарового слоя.
15. Задача ш-л для отрезка.
В наиболее общей постановке задача Ш-Л для оператора Лапласа имеет вид:


Здесь
D – область определения
уравнения (1), S – граница
области D,
 одновременно. Рассмотрим общую постановку
задачи для отрезка. Найти собственные
функции уравнения
одновременно. Рассмотрим общую постановку
задачи для отрезка. Найти собственные
функции уравнения
 ,
,

и
собственные значения
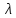 при следующих граничных условиях:
при следующих граничных условиях:


Знак «минус» в (3а) связан с тем, что
внешняя нормаль к границе S
для отрезка при
 направлена в отрицательную сторону.
направлена в отрицательную сторону.
Обозначим через
 и
и
 фундаментальную систему решений
уравнений (2). Общее решение имеет вид:
фундаментальную систему решений
уравнений (2). Общее решение имеет вид:

Подставим решение (4) в граничные условия (3а) и (3b):


Выражение (5) можно рассматривать как
систему алгебраических уравнений
относительно неизвестных
 и
и
 .
В случае, если эта система имеет
единственное решение, оно равно:
.
В случае, если эта система имеет
единственное решение, оно равно:
 .
Это решение является тривиальным и не
представляет никакого интереса с
физической точки зрения. По этой причине
потребуем, чтобы система (48) имела
множество решений. Это возможно в том
случае, если определитель, составленный
из коэффициентов системы (5), был равен
нулю:
.
Это решение является тривиальным и не
представляет никакого интереса с
физической точки зрения. По этой причине
потребуем, чтобы система (48) имела
множество решений. Это возможно в том
случае, если определитель, составленный
из коэффициентов системы (5), был равен
нулю:


Уравнение (6) записано относительно λ и
называется дисперсионным уравнением.
Система решений
 уравнения (6) образует спектр собственных
значений задачи Ш-Л.
уравнения (6) образует спектр собственных
значений задачи Ш-Л.
Найдем собственные функции задачи Ш-Л. В силу равенства нулю определителя (6) уравнения системы (5) являются равносильными. Выберем, первое уравнение системы (5). Его решение имеет вид:

Подставляя полученный результат в (4), имеем:

Функция (7) является собственной функцией задачи Ш-Л для отрезка.
16. Задача ш-л для отрезка с периодическими граничными условиями.
Рассмотрим задачу

Общее
решение уравнения имеет вид:

Подставим общее решение в граничные
условия
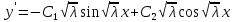
Пользуясь линейной независимостью
функций
 и
и
 и применяя известные тригонометрические
формулы, получим систему уравнений
и применяя известные тригонометрические
формулы, получим систему уравнений

Эта система уравнений имеет ненулевое решение при условии

или
 ;
;

Из последнего соотношения находим спектр собственных значений

При найденных
 система, полученная из граничных условий,
будет иметь два линейно независимых
ненулевых решения:
система, полученная из граничных условий,
будет иметь два линейно независимых
ненулевых решения:

Находим собственные функции:


17. Задача Штурма-Лиувиля для прямоугольника и прямоугольного параллелепипеда.
Прям-к.
Найти собственные функции уравнения

с граничными условиями


Здесь
 и
и
 – постоянные, причем
– постоянные, причем

Для решения задачи (1) – (2) воспользуемся
методом разделения переменных. Представим
функцию u в виде
произведения:

Подставляя (3) и выполняя преобразования, запишем:

Граничные условия (2) принимают вид:


Соотношения (4) – (5) можно рассматривать как две задачи Ш-Л для отрезка.

Тогда собственные значения
 задачи Ш-Л для прямоугольника есть сумма
собственных значений
задачи Ш-Л для прямоугольника есть сумма
собственных значений
 и
и
 соответствующих задач для отрезка,
собственная функция задачи Ш-Л для
прямоугольника есть произведения
соответствующих собственных функций
для отрезка:
соответствующих задач для отрезка,
собственная функция задачи Ш-Л для
прямоугольника есть произведения
соответствующих собственных функций
для отрезка:


Прямоугольного парал-да. Найти решение уравнения

с граничными условиями
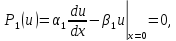





После первого разделения переменных задача (7) – (8) сведется к задачам Ш-Л для отрезка и прямоугольника. Соб ф и соб знач задачи для прям-ого парал-да имеют вид

Здесь
 ,
,

 – собственные функции и собственные
значения соответствующих одномерных
задач Ш-Л по каждой переменной.
– собственные функции и собственные
значения соответствующих одномерных
задач Ш-Л по каждой переменной.
