4. Математическое описание автоматических систем

Любая система радиоавтоматики (РА) состоит из ряда элементов (звеньев). Для каждого элемента характерна связь между его входом и выхо- дом. Эта связь выражается дифференциальным уравнением. Система РА в це- лом описывается системой дифференциальных уравнений.

4.1. Составление дифференциального уравнения элемента автоматической системы

Конкретный вид дифференциального уравнения зависит от физи-

ческой природы и свойств элемента.

Рассмотрим в качестве примера инерционную RC- цепь (рис.4.1):

_{Рис.4.1. Схема инерционного звена}

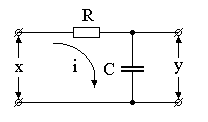
_Здесь

_{x  iR  y ;}

_{i } ^dQ _{ C} ^dy

_{; отсюда}

_{x  RC} ^dy _{ y .}

dt

Обозначим RC = T. Тогда

dt dt

_{x  T} ^dy _{ y .}

^dt

_d

Введем символ дифференцирования

_{p  и запишем полученное}

dt

уравнение в символической форме :

_x

x  Tpy  y . Вынесем y за скобки и

₁

окончательно получим

_{y }

^{pT 1}

₁

_{ x .}

^{1 pT}

Отметим, что выражение

_{1 pT}

называется операторным коэффициентом пе-

редачи инерционного (в данном случае) звена.

4.2. Статические и динамические свойства элементов

После подачи на вход элемента некоторого воздействия на его выходе возникает переходный процесс, по окончании которого наступает стационарное состояние.

Статическая характеристика- это зависимость, связывающая между со-

бой стационарные входную и выходную величины.

Примером статической характеристики может служить зависимость ме-

жду напряжением на выходе частотного дискриминатора и отклонением часто-

ты сигнала от его номинального значения (рис.4.2).

Динамическая характеристика - это зависимость, связывающая между собой приращения входной и выходной величин в переходном режиме.

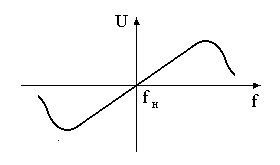
Рис.4.2. Статическая характеристика дискриминатора

4.3. Преобразование Лапласа

Преобразование Лапласа имеет две формы:

_{- прямое преобразование}

X ( p) 

jω

изображение по оригиналу функции;

_{- обратное преобразование}

_

_ ^{x(t )  e  pt dt , которое позволяет найти}

0

_{x(t) }

₁ ^{c }

_

_{X ( p)e} ^pt _{dp , которое позволяет}

^2j _{c  jω}

_{отыскать оригинал функции по ее изображению.}

Здесь

_{x(t )  оригинал функции;}

_{X ( p) }

изображение функции по Ла-

пласу;

_{p  c }

_{jω - комплексная переменная.}

Существуют следующие методы отыскания оригинала:1) табличный, 2)

метод интегрирования в комплексной плоскости.

Рис.4.3. Примеры описания звеньев в операторной форме

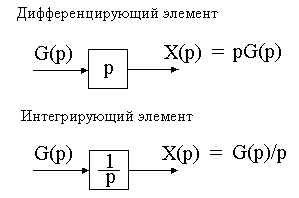
Преобразование Лапласа позволяет осуществить переход от исходных дифференциальных уравнений системы РА к алгебраическим уравнениям.

4.4. Преобразование Фурье

Заменим в преобразовании Лапласа оператор

_{перейдем к преобразованию Фурье:}

p на переменную jω -

x( jω) 

^ _

 ^x(t)e

_{ }

^jωdt ;

x( jω)

называется спектральной функцией воздействия

_{Обратное преобразование Фурье имеет вид:}

x(t ).



_{x(t) } ¹

^ _{x( jω)e} ^jωt _{dω .}

^2 _{ }

Преобразование Лапласа описывает как переходное, так и стационарное

состояние процесса.

Преобразование Фурье описывает стационарное состояние процесса в частотной области.

4.5. Передаточная функция

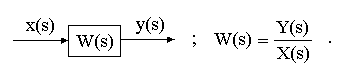
Отношение изображения Y(s) выходной величины элемента (системы) к изображению X(s) входной величины при нулевых начальных условиях назы- вается передаточной функцией элемента (системы).

Формально передаточная функция получается из дифференциального уравнения элемента (системы) в символической форме путем замены в нем символа p на комплексную переменную s и деления образованного таким об- разом многочлена правой части уравнения на многочлен левой части.

Например, если дифференциальное уравнение инерционного

_{мента имеет вид (см. п. 4.1)}

RC - эле-

_{x( t ) = RC} ^{dy( t )} _{+ y( t );}

^dt

x( p ) = Tpy( p ) + y( p ) = y( p )( Tp + 1 );

то получаем

W ( s ) =

^{Y ( s )} ₌

^{X ( s )}

¹ _.

^{Ts + 1}

Здесь

X ( s ) и Y ( s ) - изображения по

Лапласу

x ( s ) и

y ( s ) .

4.6. Переход от передаточной функции к частотной характеристике

В общем виде передаточная функция записывается так:

_{W ( s ) =} ^{kQ( s )} _,

^{P( s )}

где

_{Q( s ) - многочлен в числителе,}

_{P( s )}

_{- многочлен в знаменателе, k }

по-

стоянный множитель.

Заменим комплексную переменную s на комплексную частоту

_{jω ,-}

_{получим амплитудно-фазо-частотную характеристику элемента (системы):}

_{W ( jω) } ^{kQ( jω)} _.

P( jω)

Например, передаточная функция последовательного соединения безы-

нерционного усилителя с коэффициентом усиления k и инерционной RC - це-

_{пи имеет вид}

Заменим s на

_{jω :}

W ( s ) =

_k

_.

^{Ts + 1}

_{W ( jω) } ^k

_ ^{k (1}

^{jωT )} _{ W (ω)e} ^{j (ω)} _.

jωT 1

_{1 ω} ²_T ²

_{|W ( ) |} ^k

1 ω²T ²

- это модуль комплексного выражения или, иначе,

амплитудно-частотная характеристика данного элемента;

() = - arctg (T) - это аргумент комплексного выражения или, иначе, фазо-

_{частотная характеристика элемента.}

_{Запишем W ( jω)}

в алгебраической форме:

W ( jω)  U (ω) 

jV (ω).

Здесь

U (ω) - вещественная частотная характеристика,

V (ω) - мнимая

частотная характеристика.

В случае замкнутой системы РА передаточная функция обозначается через Ф ( s ) , а амплитудно-фазо-частотная характеристика - через

_{Ф( jω)  P(ω) }

_jQ(ω),

где

_P(ω)

_{и Q(ω) - соответственно вещественная и}

_{мнимая частотные характеристики замкнутой системы.}

4.7. Логарифмические частотные характеристики

В реальных автоматических системах модуль частотной характеристики изменяется в очень широких пределах при изменении частоты. Поэтому прак- тическое изображение их в обычном масштабе невозможно. В этих случаях удобно пользоваться логарифмическими частотными характеристиками: ам- плитудной и фазовой.

_{Логарифмическая амплитудно-частотная характеристика определяется}

_{соотношением L(ω)  20lgW (ω) , где}

_{L(ω) }

_{в децибелах, а частота ω}

откла-

_{дывается в декадах или в октавах. Логарифмическая фазо-частотная характери-}

стика

_{ (ω)}

отображается в градусах, а частота - в декадах или в октавах

_{(рис.4.4).}

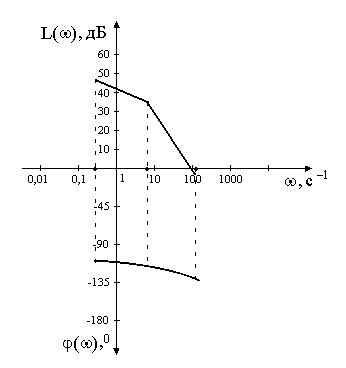
Рис.4.4. Логарифмические амплитудно-фазо-частотные характеристики

Контрольные вопросы

1. Что такое операторный коэффициент передачи звена (системы) ра-

диоавтоматики ?

2. Чем отличается динамическая характеристика звена (системы) радио-

автоматики от статической характеристики ?

_{3. В чем состоит отличие преобразования Фурье от преобразования Лап-}

ласа ?

_{4. Что такое передаточная функция автоматической системы и что она}

характеризует ?

5. Какие динамические характеристики системы радиоавтоматики вы можете назвать ?