16. Качество процессов в линейных импульсных системах

Основные показатели качества процессов в импульсных системах такие

же, как и в непрерывных автоматических системах: время регулирования t_p, ве-

личина перерегулирования  и число перерегулирований п (показатели качест-

ва переходного процесса); точность работы систем в установившихся режимах.

В чем же особенности исследования качества импульсных автоматиче-

ских систем?

Оценку показателей качества переходного процесса производят по им-

пульсной переходной функции системы h (пТ) — реакции на единичную сту-

^{пенчатую дискретную функцию Х}_вх ^{(nТ) = 1 (пТ).}

Изображение реакции системы в смысле Z-преобразования находят по

_{формуле (14)}

^Х _вых ^{( z) }

^X _вх ^{( z)  Ф( z) .}

_{Так как изображение единичной дискретной функции}

^Х вх

^{( z)  Z} ^{1nT }^

_z

^,

z 1

_{то изображение дискретной переходной функции импульсной системы}

^{H ( z)  Z} ^{hnT }^

z

z 1

Ф( z) .

Как видно из этой формулы, изображение можно представить в общем случае в виде отношения двух полиномов.

Следовательно, для нахождения Н (z) достаточно знать передаточную функцию замкнутой системы Ф (z).

Далее, необходимо по изображению найти оригинал h (пТ), т. е. осуще-

ствить операцию обратного Z-преобразования. Эту задачу часто решают мето-

дом разложения функции в степенной ряд по отрицательным степеням z (деле- нием полинома числителя на полином знаменателя). Коэффициенты получен- ного степенного ряда равны дискретным значениям импульсной переходной функции в моменты времени t = пТ. Другой метод требует разложения Н (z)

на простые дроби.

Рассмотрим на примере методику оценки показателей качества переход-

ных процессов импульсной системы, изображенной на рис.14.1, при различных

значениях ее параметров k_v и Т. Изображение переходной функции системы с учетом формулы (19)

H ( z) 

z

z 1

Ф( z) 

^{k vTz} _.

^{z 2  z(k} _v^{t  2) 1 k} _v^T

^{1. При k}_v^{T= 1,5 изображение переходной функции системы}

_1,5z

H ( z) 

_.

_z ² _{ 0,5z  0,5}

В результате деления числителя на знаменатель находим:

_{H ( z)  1,5z} ^1 _{ 0,75z} ^{ 2}

_{ 1,125z} ^{ 3} _{ 0,937 z} ^{ 4}

_{ 1,03z} ^{ 5} _{ ...}

Коэффициенты степенного ряда определяют следующие значения дис-

_{кретной переходной функции-оригинала:}

h(0)  0,

h(T )  1,5,

h(2T )  0,75,

h(3T )  1,125,

h(4T )  0,937,

_{h(5T )  1,03}

и т.д.

График переходной функции для этого случая изображен на рис.16.1, а.

Анализ графика позволяет определить показатели качества переходного про-

цесса: t_p = 5Т сек; = 50%; п = 4.

Очевидно, что для уменьшения величины перерегулирования необходи-

мо уменьшать произведение k _vТ.

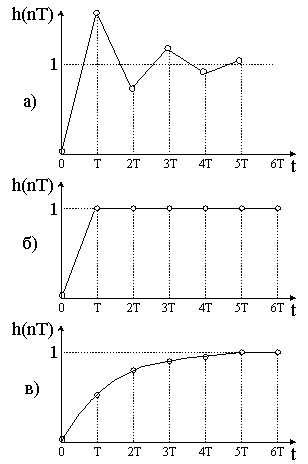
Рис.16.1. Переходные функции импульсной системы

^{2. При k} _v ^{Т = 1 изображение переходной функции системы}

H ( z) 

₁

^

z 1

z ^1  z ^{ 2}  z ^3  z ^{ 4}  .. .

Дискреты переходной функции:

h(0)=0; h(T)=1; h(2T)=1.

Из графика переходной функции, представленного на рис.16.1,б, видно,

что при k_v Т = 1 в системе имеет место оптимальный по быстродействию пере- ходный процесс, так как он завершается за один период дискретности Т без пе- ререгулирования.

3. При k _v Т = 0,5 имеем:

H ( z) 

0,5z

_z ² _{1,5z  0,5}

 0,5z ^1  0,75z ^{ 2}  0,875z ^{ 3}  0,938z ^{ 4}  ..

Отсюда находим:

h(0) = 0; h(T) = 0,5; h(2T) = 0,75; h(3T) = 0,875; …

График этой функции, изображенный на рис. 16.1, в, близок к экспонен-

те. Время регулирования в этом случае t_p = 5Тсек.

Проведенный анализ позволяет сделать важный вывод о том, что пока-

затели качества переходного процесса импульсной системы существенно зави-

сят от величины произведения коэффициента передачи k_v на период дискрет-

ности Т.

Точность импульсной системы оценивается величиной ошибки в устано-

вившихся режимах. Для расчета ошибки необходимо знать изображение за-

дающего воздействия и передаточную функцию ошибки Ф_ (z). Методика вы-

числения дискретной функции  (nT) аналогична изложенной выше.

Контрольные вопросы

1. Какими показателями оценивается качество работы дискретных авто-

матических систем ?

_{2. Как определяется дискретная переходная функция импульсной систе-}

мы ?

_{3. Каким способом можно для импульсной системы определить величи-}

ну ошибки в установившемся режиме ?