
- •Санкт-Петербург
- •Введение
- •1. Основные понятия и определения
- •2. Классификация систем радиоавтоматики
- •3. Типовые системы радиоавтоматики
- •4. Математическое описание автоматических систем
- •5. Типовые входные сигналы
- •5.5. Белый шум
- •6. Переходная и импульсная переходная функции
- •7. Типовые линейные звенья и их соединения
- •7.1. Усилительное звено
- •7.2. Инерционное звено
- •8. Переход от функциональной схемы системы ра к ее структурной схеме
- •9. Правила структурных преобразований
- •10. Функциональные и структурные схемы систем радиоавтоматики
- •11. Импульсные системы радиоавтоматики
- •12. Понятие о дискретных функциях и разностных уравнениях
- •13. Дискретное преобразование Лапласа и z – преобразование
- •14. Передаточные функции импульсных автоматических систем
- •15. Оценка устойчивости импульсной автоматической системы
- •16. Качество процессов в линейных импульсных системах
- •17. Цифровые системы радиоавтоматики
- •18. Цифровая фильтрация
- •8. Переход от функциональной схемы системы ра к ее
- •10. Функциональные и структурные схемы систем
- •12.Понятие о дискретных функциях и разностных
- •14. Передаточные функции импульсных автоматических
- •15. Оценка устойчивости импульсной автоматической
14. Передаточные функции импульсных автоматических систем
Структурные представления и передаточные функции составляют осно-
ву для инженерных расчетов импульсных автоматических систем. Они позво-
ляют в значительной степени облегчить решение задач исследования.
Для исследования динамических свойств системы в первую очередь не-
обходимо определить ее передаточные функции, которые, как известно, уста-
навливают зависимость между входным воздействием и реакцией системы
(звена). Обычно в рассмотрение вводят, как и при исследовании непрерывных систем, следующие передаточные функции: передаточную функцию разомкну-
той импульсной системы и передаточную функцию ошибки.
Передаточной функцией разомкнутой импульсной системы называется отношение изображений в смысле дискретного преобразования Лапласа вы-
вых
X ( p)
W ( p)
.
E ( p)
Аналогично определяется эта передаточная функция в смысле Z – пре-
образования:
W ( z)
X вых ( z) .
E( z)
Основная задача состоит в том, чтобы определить передаточную функ-
цию W(z) по известной передаточной функции приведенной непрерывной час-
ти системы W(p). Эту задачу решают в следующей последовательности:
1. По передаточной функции W(p) в результате применения обратного преобразования Лапласа находят функцию веса ПНЧ:
w(t ) L1W ( p).
2. По функции веса ПНЧ w(t) определяют аналитическое выражение для соответствующей дискретной функции веса w(nТ).
3. Искомую передаточную функцию W(z) получают как Z –
преобразование дискретной функции веса ПНЧ:
W ( z) Z w(nT ).
Основная передаточная функция замкнутой импульсной системы позво-
ляет вычислить реакцию замкнутой системы хвых(пТ) на задающее воздействие хвх(пТ). Ее определяют, как и в непрерывных системах, в соответствии с урав- нением замыкания через дискретную передаточную функцию разомкнутой системы:
Ф( z)
xвых ( z)
xвх ( z)
W ( z)
.
1W ( z)
(14)
Передаточную функцию замкнутой системы всегда можно представить в
виде отношения двух полиномов относительно переменной z:
Ф( z)
bk z k
bk 1z
k 1
...b1z b0 .
(15)
m
cm z
cm 1z
m 1
... c1z
c0
Запишем это выражение в развернутом виде :
(cm z m
... c1z c0 ) X вых ( z) (bk z k
... b1z b0 ) X вх ( z).
(16)
Левая часть этого уравнения (в скобках) представляет собой характери-
стический полином замкнутой импульсной системы М (z).
В результате перехода от изображений к оригиналам в формуле (16) лег-
ко получить соответствующее разностное уравнение системы:
cm X вых (nT
mT ) ..... c1 X вых nT T c0 X вых (nT )
bk X вх (nT
kT ) .....b1X вх (nT
T ) b0 X вх (nT ).
Аналогично можно получить разностное уравнение разомкнутой систе-
мы по передаточной функции W(z).
Передаточная функция ошибки определяется через передаточную функ-
цию разомкнутой системы по формуле
Фε ( z)
Е( z)
X вх ( z)
1
1W ( z)
. (17)
Зная задающее воздействие и эту передаточную функцию, можно оце-
нить динамическую точность импульсной системы — найти дискретную функ-
цию ошибки (nТ).
Рассмотрим конкретный пример определения передаточных функций импульсной системы. Определим передаточные функции системы, структурная схема которой изображена на рис.14.1.
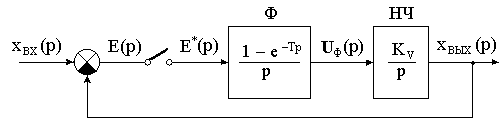
Как видно из рисунка, в прямой цепи системы имеется простейший им-
пульсный элемент (фиксатор) и непрерывная часть (интегрирующее звено).
Передаточная функция приведенной непрерывной части:
W ( р)
Х вых ( р)
Wф ( p)Wн ( p) k v
1 e pT
.
2
Е ( р) p
Дискретную передаточную функцию разомкнутой системы находим в соответствии с методикой, изложенной выше:
W ( z)
X вых
( z)
k
z 1 1
Z
k vT
. (18)
E( z)
v z p 2
z 1
Разностное уравнение разомкнутой системы определяем, в случае необ-
ходимости, непосредственно из формулы (18):
Х вых (nT T ) X вых (nT ) k vTε(nT ) .
Зная W (z), легко найти основную передаточную функцию замкнутой системы :
Ф( z)
Х вых ( z)
X вх ( z)
W ( z)
1W ( z)
k vT
z (k vT 1)
(19)
и передаточную функцию ошибки:
Фε ( z)
E( z)
X вх ( z)
1
1W ( z)
z 1
z (k vT 1)
. (20)
Динамические процессы в замкнутой импульсной системе описываются
следующим разностным уравнением, полученным из формулы (19) путем пе-
рехода к оригиналам:
Х вых (nT T ) (k vT 1) X вых (nT ) k vTX вх (nT ) .
Контрольные вопросы
1. Какие передаточные функции обычно используют при исследовании импульсных систем радиоавтоматики и почему ?
2. Как определяют передаточную функцию замкнутой импульсной сис-
темы ?
3. Как определяется дискретная передаточная функция ошибки и для че-
го она используется ?
