12. Понятие о дискретных функциях и разностных уравнениях

Сигналы в импульсных системах могут быть представлены в виде дис-

кретных функций времени, т. е. функций, значения которых определены только

для дискретных значений аргумента t=nT. Между этими значениями независи-

мой переменной дискретная функция равна нулю.

Дискретную функцию можно образовать из любой непрерывной функ-

ции, если принять во внимание только ее дискретные значения в равностоящие друг от друга моменты времени (рис.12.1). Эти ординаты называют дискретами.

Дискретную функцию будем обозначать символом x (nT), где T-период дискретности; n – любое целое число. Для того чтобы получить функцию

x(nT) по заданной непрерывной функции x(t), в последней необходимо заме-

нить t на nT.

Рис.12.1. Непрерывная (a) и дискретная (b) функции

Примеры непрерывных функций и соответствующих им дискретных функций приведены ниже.

Непрерывная функция Дискретная функция

x(t) x(nT)

1(t) 1(nT) At AnT At² A(nT)²

_e ^{–a t} _e ^{–a nT}

sin_ct sin_cnT

Заметим, что дискретная функция не является однозначной: ей могут соответствовать различные непрерывные или разрывные функции, если только

их ординаты в моменты времени t = nT равны значениям функции x(nT). Для устранения этой неоднозначности в рассмотрение вводят смещенные дискрет- ные функции, позволяющие «просматривать» процессы внутри периодов дис- кретности Т.

_{Иногда оказывается удобным перейти к относительному масштабу вре-}

_{_}

мени

_нице.

_{t } ^t

^T

. При этом интервал между дискретами становится равным еди-

Как известно, скорость изменения непрерывной функции определяется

ее первой производной. Скорость изменения дискретной функции x(nT) ха- рактеризуется ее первой разностью, деленной на период дискретности Т. Сле- довательно, аналогом дифференциалов для дискретных функций являются разности, а интегралов – суммы.

Первая разность, или разность первого порядка, дискретной функции x(nT)  x(nT) = x(nT+Т) - x(nT) также является дискретной функцией времени.

Вторая разность, или разность второго порядка, определяется как первая разность от первой разности:

² x(nT) = x(nT+Т) - x(nT),

или ² x(nT) = x(nT+2Т) - 2 x(nT+Т) + x(nT).

Разность k – го порядка ^k x(nT) = ^k-1 x(nT+Т) - ^k-1x(nT).

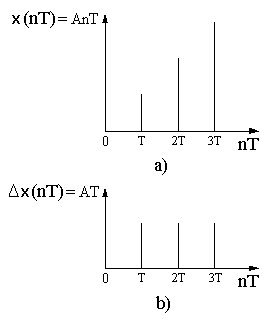
Рис.12.2. Дискретная функция (a) и ее первая разность (b)

Рассмотрим пример. Дана дискретная функция x(nT)=AnT (рис.12.2).

Ее первая разность  x(nT) = А(nT+Т) – АnT = АТ является единичной

ступенчатой дискретной функцией. Вторая и высшие разности этой функции

равны нулю.

Часто на практике вычисляют запаздывающую разность, которую легче получить техническими средствами:

x(nT)=x(nT)-x(nT-T)=x(nT)e^-pT.

Известно, что исследование динамики непрерывных систем основано на

составлении и решении дифференциальных уравнений. Динамические процессы

в дискретных автоматических системах описываются разностными уравнениями,

или уравнениями в конечных разностях. Линейное неоднородное разностное уравнение с постоянными коэффициентами имеет следующий вид:

c_m^mx_вых(nT) + c_m-1^m-1x_вых(nT) + … + c₁x_вых(nT) + c₀x_вых(nT) =

^b₀^x_вх^{(nT) + b}₁^x_вх^{(nT) + … + b}_k-1^k-1x_вх^{(nT) +b}_k^kx_вх^(nT),

^{где х}_вх^{(nT) – известная дискретная функция (задающее воздействие); х}_вых^{(nT) –}

дискретная функция, определяемая уравнением (решение);  - разности I – х

порядков; b_i и c_i – постоянные коэффициенты.

Контрольные вопросы

1. Что такое дискретная функция времени ?

2. Что является аналогами дифференциалов и интегралов при использо-

вании дискретных функций времени ?

3. Чем описываются динамические процессы в дискретных системах ра-

диоавтоматики ?