58. Ознака Даламбера

Якщо для ряду з додатними членами існує границя тоді: при ряд збігається;при ряд розбігається;при питання про збіжність ряду ознака не вирішує.

59.Ознака збіжності рядуДля того щоб ряд збігався, необхідно, щоб загальний член ряду прямував до нуля, тобто щоб виконувалась умова

. (6)

Доведення. Нехай ряд збігається, тобто існує границя частинних сум ряду

З рівності u_n = S_n – S_n–1 випливає, що існує границя

що і доводить правильність теореми.Умова (6) не є достатньою для збіжності ряду, що можна бачити на прикладі так званого гармонійного ряду

64.Радіус збіжності

Означення. Інтервалом збіжності степеневого ряду називається такий інтервал, у всіх внутрішніх точках якого ряд збігається абсолютно, а для всіх точок ряд є розбіжним; при цьому число R > 0 називається радіусом збіжності степеневого ряду.

Виведемо формулу для знаходження радіуса збіжності ряду. Для цього побудуємо ряд із абсолютних величин членів ряду:(1):

(2 (9.14)

Нехай існує границя . Тоді, застосовуючи ознаку Даламбера до ряду (2), дістаємо:

.

При ряд (2) збігається, а отже, ряд (1) збігається абсолютно; при ряд (2) розбігається. Розбіжність ряду, установлена за ознакою Даламбера, означає, що для цього ряду не виконується необхідна умова збіжності: , а тому не виконується необхідна умова збіжності і для ряду (1) , і ряд (1) при буде також розбіжним. Отже, нерівність визначає інтервал збіжності ряду (2): . Радіус збіжності визначається за формулою

. (9.15)

Аналогічно, використовуючи радикальну ознаку Коші, можна дістати формулу для радіуса збіжності, степеневого ряду у вигляді: .

65..Наближене інтегрування за доп.рядів

Степеневий ряд

буде рівномірно збіжним на будь-якому відрізку із його інтервалу збіжності , а тому на такому відрізку його можна почленно інтегрувати та диференціювати, при цьому мають місце рівності:

74. Структура заг.Розв.Лінйного неоднорідного др.

Шукаємо загальний розв’язок неоднорідного ДР у вигляді .

Оскільки виконується тотожність, то для відшукання z маємо однорідне ДР

Отже, справджується така теорема:

Теорема 1. Загальний розв’язок неоднорідного лінійного ДР дорівнює сумі частинного розв’язку неоднорідного ДР і загального розв’язку однорідного ДР.

75. Метод варіації довільних сталих.

Лагранж запропонував загальний метод розв’язування неоднорідних лінійних ДР. Спочатку розв’язується однорідне ДР. У загальний розв’язок входять довільні сталі. Потім шукається загальний розв’язок неоднорідного ДР і при цьому довільні сталі стають новими шуканими функціями.Шукатимемо розв’язок неоднорідного ДР (8.29).

Спочатку розв’яжемо однорідне ДР . Загальний розв’язок має вигляд . Шукаємо розв’язок неоднорід­ного ДР у вигляді Підставляючи в ДР (8.28), дістаємо рівняння

.Приходимо до простого ДР

і загального розв’язку неоднорідного ДР виду (8.30):

Метод Лагранжа часто називають методом варіації довільної сталої.

79. Розв.лінійного неоднорідного рівняння н-го порядку.

ДР виду

називається лінійним ДР n-го порядку. Якщо то ДР називається однорідним, якщо то ДР називається неоднорідним.

80. Системи ДР

ДР

завжди можна звести до системи рівнянь виду

(8,54) (8.54)

Загальний розв’язок системи рівнянь (8,54) має вигляд

де — довільні сталі. Система рівнянь

визначає s-й частинний розв’язок системи рівнянь (8.54). Ці розв’язки будуть лінійно незалежні, якщо

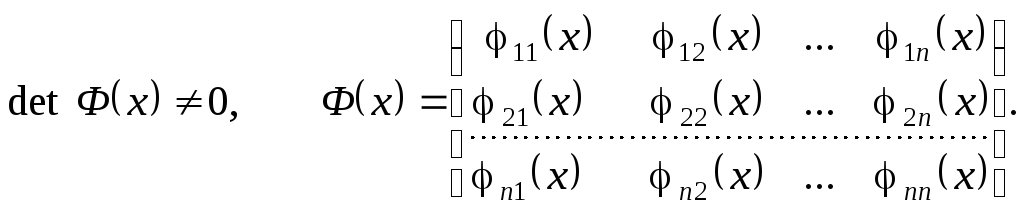
Матриця Ф(х) називається фундаментальною матрицею роз­в’язків. Загальний розв’язок можна записати у векторній формі

Систему рівнянь (8.54) часто можна звести до одного ДР n-го порядку, що можна використати для розв’язання системи ДР.

81.Метод Ейлера.

Домножуємо рівняння на інтегрувальний множник Дістаємо ДР

Нехай ДР набирає вигляду:

.

Остаточно приходимо до розв’язку виду

: