
Показательный тренд
Исходные данные
|
Средние цены на первичном рынке жилья на элитные квартиры y |
t |
lny |
|
7739 |
1 |
8,9540 |
|
10077 |
2 |
9,2180 |
|
13413 |
3 |
9,5040 |
|
14826 |
4 |
9,6041 |
|
17968 |
5 |
9,7963 |
|
23899 |
6 |
10,0816 |
|
30063 |
7 |
10,3111 |
|
34518 |
8 |
10,4492 |
|
50175 |
9 |
10,8233 |
|
65854 |
10 |
11,0952 |
|
69612 |
11 |
11,1507 |
|
65617 |
12 |
11,0916 |
|
69351 |
13 |
11,1469 |
y=8,8633*0,1978t
Средняя ошибка аппроксимации
В данном случае:
|
t |
Lny (фактическая) |
Остатки |
Отклонение, % |
|
|
1 |
8,9540 |
-0,107091928 |
1,20% |
|
|
2 |
9,2180 |
-0,040948708 |
0,44% |
|
|
3 |
9,5040 |
0,04718018 |
0,50% |
|
|
4 |
9,6041 |
-0,050501708 |
0,53% |
|
|
5 |
9,7963 |
-0,056131604 |
0,57% |
|
|
6 |
10,0816 |
0,031272716 |
0,31% |
|
|
7 |
10,3111 |
0,062891381 |
0,61% |
|
|
8 |
10,4492 |
0,003237229 |
0,03% |
|
|
9 |
10,8233 |
0,179433299 |
1,66% |
|
|
10 |
11,0952 |
0,253516676 |
2,28% |
|
|
11 |
11,1507 |
0,111173573 |
1,00% |
|
|
12 |
11,0916 |
-0,145768483 |
1,31% |
|
|
13 |
11,1469 |
-0,288262623 |
2,59% |
|
|
Средняя ошибка аппроксимации, % |
1,00% |
|||
Средняя ошибка аппроксимации составила 1,00.
Таким образом, можно говорить о высокой точности модели.
F критерий Фишера
F = 327,6081 (>Fкр = 4,8443 из таблицы распределения Фишера-Снедекора (F-распределение)). Таким образом, можно сделать вывод о значимости уравнения регрессии.
Автокорреляция в остатках. Критерий Дарбина-Уотсона
Автокорреляция в остатках была найдена с помощью пакета анализа в Exel и составила 0,6998. Оценим ее существенность с помощью критерия Дарбина-Уотсона.
|
t |
Остатки |
et-1 |
et-1^2 |
(et-et-1)^2 |
et^2 |
||
|
1 |
-0,10709193 |
|
|
|
0,011469 |
||
|
2 |
-0,04094871 |
-0,107091928 |
0,011469 |
0,004375 |
0,001677 |
||
|
3 |
0,04718018 |
-0,040948708 |
0,001677 |
0,007767 |
0,002226 |
||
|
4 |
-0,05050171 |
0,04718018 |
0,002226 |
0,009542 |
0,00255 |
||
|
5 |
-0,0561316 |
-0,050501708 |
0,00255 |
3,17E-05 |
0,003151 |
||
|
6 |
0,031272716 |
-0,056131604 |
0,003151 |
0,00764 |
0,000978 |
||
|
7 |
0,062891381 |
0,031272716 |
0,000978 |
0,001 |
0,003955 |
||
|
8 |
0,003237229 |
0,062891381 |
0,003955 |
0,003559 |
1,05E-05 |
||
|
9 |
0,179433299 |
0,003237229 |
1,05E-05 |
0,031045 |
0,032196 |
||
|
10 |
0,253516676 |
0,179433299 |
0,032196 |
0,005488 |
0,064271 |
||
|
11 |
0,111173573 |
0,253516676 |
0,064271 |
0,020262 |
0,01236 |
||
|
12 |
-0,14576848 |
0,111173573 |
0,01236 |
0,066019 |
0,021248 |
||
|
13 |
-0,28826262 |
-0,145768483 |
0,021248 |
0,020305 |
0,083095 |
||
|
|
0,177032 |
0,239187 |
|||||
Критерий Дарбина-Уотсона
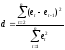
В нашем случае d = 0,177031707 / 0,239186783 = 0,7401
|
0 |
0,7401 |
1,01 |
1,34 |
2 |
2,66 |
2,99 |
4 |
|
|
d |
dl |
du |
|
du |
dl |
|
d<dl =>Есть положительная автокорреляция в остатках. Значит в выборке есть тенденция.
|
ВЫВОД ИТОГОВ |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Регрессионная статистика |
|
|
|
|
|
|
|
|||||||||||
|
Множественный R |
0,98362293 |
|
|
|
|
|
|
|
||||||||||
|
R-квадрат |
0,967514069 |
|
|
|
|
|
|
|
||||||||||
|
Нормированный R-квадрат |
0,964560803 |
|
|
|
|
|
|
|
||||||||||
|
Стандартная ошибка |
0,147459326 |
|
|
|
|
|
|
|
||||||||||
|
Наблюдения |
13 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Дисперсионный анализ |
|
|
|
|
|
|
|
|
||||||||||
|
|
df |
SS |
MS |
F |
Значимость F |
|
|
|
||||||||||
|
Регрессия |
1 |
7,123593823 |
7,123593823 |
327,6081195 |
1,55513E-09 |
|
|
|
||||||||||
|
Остаток |
11 |
0,239186783 |
0,021744253 |
|
|
|
|
|
||||||||||
|
Итого |
12 |
7,362780606 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
Нижние 95,0% |
Верхние 95,0% |
||||||||||
|
Y-пересечение |
8,863279789 |
0,08675746 |
102,1615874 |
9,87552E-18 |
8,672327908 |
9,05423167 |
8,672327908 |
9,05423167 |
||||||||||
|
t |
0,197839898 |
0,010930412 |
18,09994805 |
1,55513E-09 |
0,173782223 |
0,221897574 |
0,173782223 |
0,221897574 |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
ВЫВОД ОСТАТКА |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Наблюдение |
Предсказанное lny |
Остатки |
|
|
|
|
|
|
||||||||||
|
1 |
9,061119688 |
-0,107091928 |
|
|
|
|
|
|
||||||||||
|
2 |
9,258959586 |
-0,040948708 |
|
|
|
|
|
|
||||||||||
|
3 |
9,456799485 |
0,04718018 |
|
|
|
|
|
|
||||||||||
|
4 |
9,654639383 |
-0,050501708 |
|
|
|
|
|
|
||||||||||
|
5 |
9,852479281 |
-0,056131604 |
|
|
|
|
|
|
||||||||||
|
6 |
10,05031918 |
0,031272716 |
|
|
|
|
|
|
||||||||||
|
7 |
10,24815908 |
0,062891381 |
|
|
|
|
|
|
||||||||||
|
8 |
10,44599898 |
0,003237229 |
|
|
|
|
|
|
||||||||||
|
9 |
10,64383888 |
0,179433299 |
|
|
|
|
|
|
||||||||||
|
10 |
10,84167877 |
0,253516676 |
|
|
|
|
|
|
||||||||||
|
11 |
11,03951867 |
0,111173573 |
|
|
|
|
|
|
||||||||||
|
12 |
11,23735857 |
-0,145768483 |
|
|
|
|
|
|
||||||||||
|
13 |
11,43519847 |
-0,288262623 |
|
|
||||||||||||||
|
|
Линейный |
Парабола |
Степенной |
Показательный |
|
Уравнение |
y = 6045,5220x - 5925,4231 |
y = 214,5509x2 + 3041,8087x + 1583,8601 |
y = 5182,x0,977 |
y=8,8633*0,1978t |
|
R2 |
93,06%
|
94,35%
|
91,17% |
96,75% |
|
F-критерий |
+ |
+ |
+ |
+ |
|
Ошибка аппроксимации |
24,27% |
14,97% |
1,94% |
1,00% |
|
Автокоррелиция в остатках |
есть |
в зоне неопределенности |
есть |
есть |
Таким образом, наилучшим трендом является показательный.
Задача 2
|
Месяц |
Число незанятых граждан, тыс. чел. (y) |
y-1 |
Объем платных услуг населению, млрд. руб. (x) |
x-1 |
|
Январь |
44 |
|
6,5 |
|
|
Февраь |
45,5 |
44 |
7 |
6,5 |
|
Март |
46,8 |
45,5 |
7 |
7 |
|
Апрель |
47,9 |
46,8 |
7,4 |
7 |
|
Май |
48,3 |
47,9 |
7,5 |
7,4 |
|
Июнь |
49,1 |
48,3 |
7,2 |
7,5 |
|
Июль |
49,9 |
49,1 |
7,5 |
7,2 |
|
Август |
50,5 |
49,9 |
7,9 |
7,5 |
|
Сентябрь |
51,9 |
50,5 |
8,2 |
7,9 |
|
Октябрь |
52,3 |
51,9 |
8,5 |
8,2 |
|
Ноябрь |
53,5 |
52,3 |
8,9 |
8,5 |
|
Декабрь |
54,7 |
53,5 |
9,2 |
8,9 |
|
Автокорреляция y |
Столбец 1 |
Столбец 2 |
|
Столбец 1 |
1 |
|
|
Столбец 2 |
0,991167061 |
1 |
|
Автокорреляция x |
Столбец 1 |
Столбец 2 |
|
Столбец 1 |
1 |
|
|
Столбец 2 |
0,953471458 |
1 |
Коэффициент автокорреляции характеризует тесноту линейной связи предыдущего и текущего уровней ряда. По двум рассмотренным рядам динамики - Число незанятых граждан и Объем платных услуг населению коэффициент автокорреляции уровней первого порядка составил 0,9911 и 0,9534 соответственно, что демонстрирует тесную связь последующих уровней ряда от предыдущих. Значит в выборке есть тенденция.
Метод первых разностей

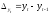

|
ВЫВОД ИТОГОВ |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
(входные данные у-1 и x-1) |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Регрессионная статистика |
|
t табл |
2,262157158 |
|
|
|
|
||||||||||||||||||
|
Множественный R |
0,95724877 |
|
F табл |
5,117355008 |
|
|
|
|
|||||||||||||||||
|
R-квадрат |
0,916325208 |
|
|
|
|
|
|
|
|||||||||||||||||
|
Нормированный R-квадрат |
0,907028009 |
|
|
|
|
|
|
|
|||||||||||||||||
|
Стандартная ошибка |
0,896078581 |
|
|
|
|
|
|
|
|||||||||||||||||
|
Наблюдения |
11 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Дисперсионный анализ |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
df |
SS |
MS |
F |
Значимость F |
|
|
|
|||||||||||||||||
|
Регрессия |
1 |
79,13884314 |
79,13884314 |
98,55927599 |
0,00000380 |
|
|
|
|||||||||||||||||
|
Остаток |
9 |
7,226611408 |
0,802956823 |
|
|
|
|
|
|||||||||||||||||
|
Итого |
10 |
86,36545455 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
Нижние 95,0% |
Верхние 95,0% |
|||||||||||||||||
|
Y-пересечение |
19,12559715 |
3,027684875 |
6,316904809 |
0,000138184 |
12,27649813 |
25,9747 |
12,2765 |
25,97469616 |
|||||||||||||||||
|
Переменная X 1 |
3,939215686 |
0,396790265 |
9,927702453 |
3,80088E-06 |
3,041613748 |
4,836818 |
3,041614 |
4,836817624 |
|||||||||||||||||

ty = 6,316904809 tx = 9,927702453 tтабл = 2,2621
Все t> tтабл следовательно все параметры уравнения не случайно отличаются от нуля, и сформировались под влиянием систематически действующего фактора. Все коэффициенты регрессии статистически значимы.
R2=0,9163
На 91,63% объем платных услуг населению объясняется числом незанятых граждан. На 8,37% объем платных услуг населению объясняется другими факторами.
F = 98,5593 Fтабл = 5,1173
F>Fтабл следовательно уравнение статистически значимо и надежно.
|
ВЫВОД ОСТАТКА |
|
|
|
|
|
|
|
|
|
Наблюдение |
Предсказанное Y |
Остатки |
|
|
1 |
44,73049911 |
-0,730499109 |
|
|
2 |
46,70010695 |
-1,200106952 |
-0,730499109 |
|
3 |
46,70010695 |
0,099893048 |
-1,200106952 |
|
4 |
48,27579323 |
-0,375793226 |
0,099893048 |
|
5 |
48,6697148 |
-0,369714795 |
-0,375793226 |
|
6 |
47,48795009 |
1,612049911 |
-0,369714795 |
|
7 |
48,6697148 |
1,230285205 |
1,612049911 |
|
8 |
50,24540107 |
0,25459893 |
1,230285205 |
|
9 |
51,42716578 |
0,472834225 |
0,25459893 |
|
10 |
52,60893048 |
-0,308930481 |
0,472834225 |
|
11 |
54,18461676 |
-0,684616756 |
-0,308930481 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Автокорреляция в остатках |
Столбец 1 |
Столбец 2 |
|
|
Столбец 1 |
1 |
|
|
|
Столбец 2 |
0,40365645 |
1 |
|
Метод
включения в уравнение регрессии фактора
времени
|
ВЫВОД ИТОГОВ |
(входные данные y x и t) |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Регрессионная статистика |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Множественный R |
0,995165 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
R-квадрат |
0,990353 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
Нормированный R-квадрат |
0,98821 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
Стандартная ошибка |
0,35183 |
|
t табл |
2,262157158 |
|
|
|
|
|
||||||||||||||||
|
Наблюдения |
12 |
|
F табл |
4,256494729 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Дисперсионный анализ |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
df |
SS |
MS |
F |
Значимость F |
|
|
|
|
||||||||||||||||
|
Регрессия |
2 |
114,3726 |
57,1863022 |
461,9820069 |
8,50549E-10 |
|
|
|
|
||||||||||||||||
|
Остаток |
9 |
1,114062 |
0,123784696 |
|
|
|
|
|
|
||||||||||||||||
|
Итого |
11 |
115,4867 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
Нижние 95,0% |
Верхние 95,0% |
|
||||||||||||||||
|
Y-пересечение |
40,36131 |
2,99449 |
13,47852582 |
2,84547E-07 |
33,5873048 |
47,13532 |
33,5873 |
47,13532 |
|
||||||||||||||||
|
t |
0,776607 |
0,108078 |
7,185586141 |
5,16311E-05 |
0,532116735 |
1,021098 |
0,532117 |
1,021098 |
|
||||||||||||||||
|
Объем платных услуг населению, млрд. руб. (x) |
0,533285 |
0,473616 |
1,12598717 |
0,289298952 |
-0,538108205 |
1,604679 |
-0,53811 |
1,604679 |
|
||||||||||||||||

ty = 13,47852582 tx = 1,12598717 tt = 7,185586141 tтабл = 2,2621
Все t> tтабл следовательно все параметры уравнения не случайно отличаются от нуля, и сформировались под влиянием систематически действующего фактора. Все коэффициенты регрессии статистически значимы.
R2=0,9904
На 99,04% объем платных услуг населению объясняется числом незанятых граждан. На 6,35% объем платных услуг населению объясняется другими факторами
F = 461,982 Fтабл = 4,2564
F>Fтабл следовательно уравнение статистически значимо и надежно.
Проверка на автокорреляцию в остатках
|
Автокорреляция |
Столбец 1 |
Столбец 2 |
|
Столбец 1 |
1 |
|
|
Столбец 2 |
0,204299002 |
1 |
|
ВЫВОД ОСТАТКА |
|
|
||
|
|
|
|
||
|
Наблюдение |
Предсказанное Число незанятых граждан, тыс. чел. (y) |
Остатки |
||
|
1 |
44,60427 |
-0,60427 |
||
|
2 |
45,64752 |
-0,14752 |
||
|
3 |
46,42413 |
0,375868 |
||
|
4 |
47,41405 |
0,485947 |
||
|
5 |
48,24399 |
0,056011 |
||
|
6 |
48,86061 |
0,239389 |
||
|
7 |
49,7972 |
0,102796 |
||
|
8 |
50,78713 |
-0,28713 |
||
|
9 |
51,72372 |
0,176282 |
||
|
10 |
52,66031 |
-0,36031 |
||
|
11 |
53,65023 |
-0,15023 |
||
|
12 |
54,58683 |
0,113175 |
||
Оценим ее существенность с помощью критерия Дарбина-Уотсона.
|
t |
Остатки |
et-1 |
et-et-1 |
(et-et-1)^2 |
et^2 |
||
|
1 |
-0,604274732 |
|
|
|
0,365147951 |
||
|
2 |
-0,147524711 |
-0,60427 |
0,45675 |
0,208620582 |
0,02176354 |
||
|
3 |
0,375868041 |
-0,14752 |
0,523393 |
0,273939972 |
0,141276784 |
||
|
4 |
0,485946608 |
0,375868 |
0,110079 |
0,012117291 |
0,236144106 |
||
|
5 |
0,056010814 |
0,485947 |
-0,42994 |
0,184844787 |
0,003137211 |
||
|
6 |
0,239389203 |
0,056011 |
0,183378 |
0,033627634 |
0,057307191 |
||
|
7 |
0,102796317 |
0,239389 |
-0,13659 |
0,018657617 |
0,010567083 |
||
|
8 |
-0,287125116 |
0,102796 |
-0,38992 |
0,152038724 |
0,082440832 |
||
|
9 |
0,176281997 |
-0,28713 |
0,463407 |
0,214746153 |
0,031075343 |
||
|
10 |
-0,36031089 |
0,176282 |
-0,53659 |
0,287931926 |
0,129823937 |
||
|
11 |
-0,150232322 |
-0,36031 |
0,210079 |
0,044133004 |
0,022569751 |
||
|
12 |
0,113174791 |
-0,15023 |
0,263407 |
0,069383307 |
0,012808533 |
||
|
|
1,500040997 |
1,114062262 |
|||||
Критерий Дарбина-Уотсона

В нашем случае d=1,500040997/ 1,114062262= 1,346460649
|
0 |
0,97 |
1,33 |
1,346460649 |
2 |
2,67 |
3,03 |
4 |
|
|
dl |
du |
d |
|
du |
dl |
|
du<d>dl => Нет положительной автокорреляции в остатках.
Таким образом, тенденция была исключена, модель статистически значима, ее можно использовать для дальнейших расчетов.
