7. Шумы. Белый шум, фликер шум, красный шум, серый шум, тепловой шум, дробовой шум.

Цвета шума — система терминов, приписывающая некоторым видам шумовых сигналов определённые цвета исходя из аналогии между спектром сигнала произвольной природы (точнее, его спектральной плотностью или, говоря математически, параметрами распределения случайного процесса) и спектрами различных цветов видимого света.

Многие из следующих определений рассматривают спектр сигнала на всех частотах.

\ Основные «цвета» шумов

Цветовые соответствия различных типов шумового сигнала определяются с помощью графиков (гистограмм) спектральной плотности, то есть распределения мощности сигнала по частотам.

Белый шум

Белый шум — это сигнал с равномерной спектральной плотностью на всех частотах и дисперсией, равной бесконечности. Является стационарным случайным процессом.

Спектр белого шума

Другими словами, такой сигнал имеет одинаковую мощность в любой полосе частот. К примеру полоса сигнала в 20 герц между 40 и 60 герц имеет такую же мощность, что и полоса между 4000 и 4020 герц. Неограниченный по частоте белый шум возможен только в теории, так как в этом случае его мощность бесконечна. На практике сигнал может быть белым шумом только в ограниченной полосе частот.

Спектр броуновского шума

Броуновский (красный, коричневый) шум

Спектральная плотность красного шума пропорциональна 1/f², где f — частота. Это означает, что на низких частотах шум имеет больше энергии, чем на высоких. Энергия шума падает на 6 децибел на октаву. Акустический красный шум слышится как приглушённый, в сравнении с белым или розовым шумом. Может быть получен путем интегрирования белого шума, а также с помощью алгоритма, симулирующего броуновское движение. Спектр красного шума зеркально противоположен спектру фиолетового

Спектр серого шума

Серый шум

Термин серый шум относится к шумовому сигналу, который имеет одинаковую субъективную громкость для человеческого слуха на всём диапазоне воспринимаемых частот. Спектр серого шума получается, если сложить спектры броуновского и фиолетового шумов. В спектре серого шума виден большой «провал» на средних частотах, однако человеческий слух субъективно воспринимает серый шум как

8. Энтропия Шеннона, кол-во информации.

Информацио́нная энтропи́я — мера неопределённости или непредсказуемости информации,

Энтропия — это количество информации, приходящейся на одно элементарное сообщение источника, вырабатывающего статистически независимые сообщения.

Шеннон предположил, что прирост информации равен утраченной неопределённости, и задал требования к её измерению:

1. мера должна быть непрерывной; то есть изменение значения величины вероятности на малую величину должно вызывать малое результирующее изменение функции;

2. в случае, когда все варианты (буквы в приведённом примере) равновероятны, увеличение количества вариантов (букв) должно всегда увеличивать значение функции;

3. должна быть возможность сделать выбор (в нашем примере букв) в два шага, в которых значение функции конечного результата должно являться суммой функций промежуточных результатов.

Поэтому функция энтропии H должна удовлетворять условиям:

1. определена и непрерывна для всех , где для всех 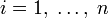и . (Нетрудно видеть, что эта функция зависит только от распределения вероятностей, но не от алфавита.)

2. Для целых положительных n, должно выполняться следующее неравенство:

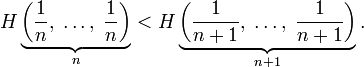
3. Для целых положительных b_i, где , должно выполняться равенство:

Шеннон показал, что единственная функция, удовлетворяющая этим требованиям, имеет вид:

где K — константа (и в действительности нужна только для выбора единиц измерения).

Шеннон определил, что измерение энтропии (), применяемое к источнику информации, может определить требования к минимальной пропускной способности канала, требуемой для надёжной передачи информации в виде закодированных двоичных чисел.

9. Принцип предпочтительности. Ряды предпочтительных чисел.

Принцип предпочтительности – один из основных принципов, используемых в стандартизации. Различают качественный и количественный аспекты применения этого принципа. Качественный аспект состоит в образовании предпочтительных рядов объектов стандартизации.

Уровней предпочтительности может быть как минимум два. В соответствии с уровнями следует выбирать по возможности более предпочтительные объекты. Как правило, наиболее предпочтительный ряд включает наименьшее количество объектов или параметров объектов стандартизации. Следующие, менее предпочтительные ряды отличаются расширенной номенклатурой и могут включать объекты предыдущих рядов. Соблюдение принципа предпочтительности позволяет добиться разумного сокращения применяемой номенклатуры стандартных объектов (элементов). Поскольку в первую очередь выбирают из наиболее предпочтительного ряда (1) и переходят к менее предпочтительным (2, 3 и др.) только если поставленная задача не имеет удовлетворительного решения на более высоком уровне, то при наличии необходимого разнообразия стандартных объектов (элементов) существенно сокращается число наиболее часто используемых решений. Стандартом установлены пять рядов R, называемых иногда рядами Ренара, которые построены на основе геометрической прогрессии со знаменателем в виде корня определенной степени из десяти (табл. 1). Ряды R5…R40 называются основными, ряд R80 – дополнительным. Наиболее предпочтительным является ряд R5, за ним следует ряд R10, и т.д. Дополнительный ряд R80 можно применять только в технически и экономически обоснованных случаях.

Структура знаменателей рядов предпочтительных чисел

Ряд	Знаменатель
R5	5 __ √10   ≈ 1,5949 (приблизительно 1,6)
R10	10 __ √10   ≈ 1,2589 (приблизительно 1,25)
R20	20__   √10   ≈ 1,1220 (приблизительно 1,12)
R40	40__   √10   ≈ 1,0593 (приблизительно 1,06)
R80	80 __ √10   ≈ 1,0292 (приблизительно 1,03)