
- •§1. Раскрытие неопределенностей с помощью правила Лопиталя. Формулировка правила Лопиталя.
- •Раскрытие неопределенностей или .
- •§2. Возрастание и убывание функции.
- •§3. Экстремумы функции.
- •§4. Наибольшее и наименьшее значения функции.
- •§5. Выпуклость и вогнутость графика функции. Точки перегиба.
- •§6. Асимптоты плоской кривой.
- •§7. Полное исследование функции и построение графика.
§5. Выпуклость и вогнутость графика функции. Точки перегиба.
График дифференцируемой
функции
![]() называется выпуклым (или выпуклым вверх)
на интервале x(a;b),
если он расположен ниже любой касательной,
проведенной к графику на этом интервале.
называется выпуклым (или выпуклым вверх)
на интервале x(a;b),
если он расположен ниже любой касательной,
проведенной к графику на этом интервале.
График функции
![]() называется вогнутым (или выпуклым вниз)
на интервале x(a;b),
если он расположен выше любой касательной,
проведенной к графику на этом интервале.
называется вогнутым (или выпуклым вниз)
на интервале x(a;b),
если он расположен выше любой касательной,
проведенной к графику на этом интервале.
Точка графика непрерывной
функции
![]() ,
отделяющая его выпуклую часть от
вогнутой, называется точкой перегиба.
,
отделяющая его выпуклую часть от
вогнутой, называется точкой перегиба.
В простейших случаях область определения функции можно разбить на конечное число интервалов с постоянным направлением выпуклости.
При x(a;х0) график выпуклый, при x(х0;b) вогнутый, М0(х0;y0) – точка перегиба.
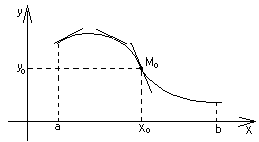
Достаточное условие выпуклости, вогнутости.
Если функция
![]() является дважды дифференцируемой и ее
является дважды дифференцируемой и ее
![]() сохраняет знак при всех x(a;b),
то график функции имеет постоянное
направление выпуклости на этом интервале:
сохраняет знак при всех x(a;b),
то график функции имеет постоянное
направление выпуклости на этом интервале:
при
![]() <0
– выпуклость вверх,
<0
– выпуклость вверх,
при
![]() >0
– вогнутость (выпуклость вниз).
>0
– вогнутость (выпуклость вниз).
Необходимое условие для точки перегиба.
Если x0
– абсцисса точки перегиба графика
функции
![]() ,
то
,
то
![]() или
или
![]() не существует.
не существует.
Необходимое условие
не является достаточным. Точки,
принадлежащие графику функции
![]() ,
в которых
,
в которых
![]() или
или
![]() не существует, называются подозрительными
на перегиб.
не существует, называются подозрительными
на перегиб.
Достаточное условие для точек перегиба.
Если вторая производная
![]() при переходе через точку х0,
подозрительную на перегиб, изменяет
знак, то точка графика с абсциссой х0
является точкой перегиба. Если
при переходе через точку х0,
подозрительную на перегиб, изменяет
знак, то точка графика с абсциссой х0
является точкой перегиба. Если
![]() не изменяет знак при переходе через
точку х0, то перегиба нет.
не изменяет знак при переходе через
точку х0, то перегиба нет.
В следующих примерах требуется определить точки перегиба и интервалы выпуклости и вогнутости графиков функций.
Пример 1.
![]() .
.
Решение.
Область
определения функции
![]() .
.
Находим
![]() ;
;
![]()
![]()
![]() .
.
![]() при х1 = 0, х2 = 1,
х3 = 3 – это точки,
подозрительные на перегиб.
при х1 = 0, х2 = 1,
х3 = 3 – это точки,
подозрительные на перегиб.
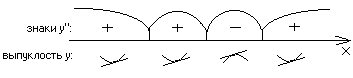
Проверяем достаточное условие выпуклости, вогнутости, точек перегиба:
При х = 1 и х = 3 есть перегибы, при х = 0 перегиба нет.
Вычисляем ординаты точек перегиба:
![]()
![]() ;
;
![]()
![]() .
.
Ответ: точки перегиба М1(1; 5,5) и М2(3; –112,5),
график вогнутый при x(–; 1) и x(3; +), график выпуклый x(1; 3).
Пример 2.
![]() .
.
Решение.
Область определения функции: x(–;+).
Находим
![]() ,
,
![]() .
.
![]() не существует при х=0, но изменяет знак
с +
на –
при переходе через х=0. Поэтому точка
графика (0;0) является точкой перегиба,
при x(–;0)
график вогнут, при x(0;+)
– выпуклый.
не существует при х=0, но изменяет знак
с +
на –
при переходе через х=0. Поэтому точка
графика (0;0) является точкой перегиба,
при x(–;0)
график вогнут, при x(0;+)
– выпуклый.

Дополнительные упражнения.
Определить интервалы выпуклости и вогнутости графиков следующих функций. Найти точки перегибов.
|
1. y=3x4–8x3+6x2+12; |
|
2. y=x3–12x2+x–1; |
|
3. y=ln(1+x2); |
|
4. y= |
|
5.
|
Ответы.
-
Точки перегиба
 и
и
 ;
при
;
при
 и
и
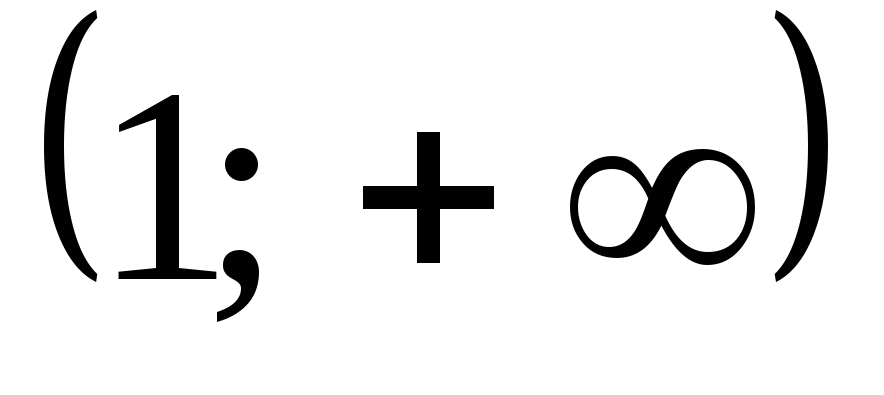 график выпуклый,
при
график выпуклый,
при
 график вогнутый.
график вогнутый.
-
Точка перегиба
 ;
при
;
при
 график выпуклый,
при
график выпуклый,
при
 график вогнутый.
график вогнутый.
-
Точка перегиба
 и
и
 ;
при
;
при
 и
и
 график выпуклый,
при
график выпуклый,
при
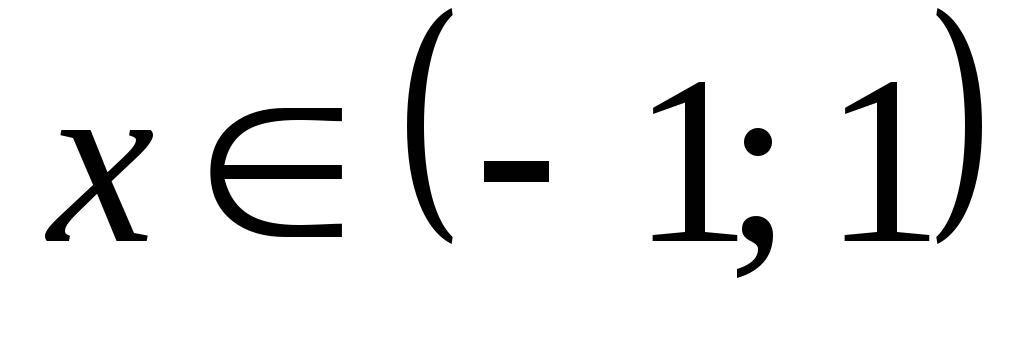 график вогнут.
график вогнут.
-
Точка перегиба
 и
и
 ;
при
;
при
 и
и
 график вогнут,
при
график вогнут,
при
 график выпуклый.
график выпуклый.
-
Точка перегиба
 ;
при
;
при
 график выпуклый,
при
график выпуклый,
при
 график вогнут.
график вогнут.
