
- •§1. Раскрытие неопределенностей с помощью правила Лопиталя. Формулировка правила Лопиталя.
- •Раскрытие неопределенностей или .
- •§2. Возрастание и убывание функции.
- •§3. Экстремумы функции.
- •§4. Наибольшее и наименьшее значения функции.
- •§5. Выпуклость и вогнутость графика функции. Точки перегиба.
- •§6. Асимптоты плоской кривой.
- •§7. Полное исследование функции и построение графика.
Тихонова В.Ф.
Практикум по высшей математике.
Приложения производной функции одной переменной. Графики.
2004
Оглавление
|
§1. Раскрытие неопределенностей с помощью правила Лопиталя. §2. Возрастание и убывание функции. §3. Экстремумы функции. §4. Наибольшее и наименьшее значения функции. §5. Выпуклость и вогнутость графика функции. Точки перегиба. §6. Асимптоты плоской кривой. §7. Полное исследование функции и построение графика. Список учебной литературы |
4 стр. 5 стр. 14 стр. 18 стр. 24 стр. 31 стр. 35 стр. 39 стр. 51 стр. |
§1. Раскрытие неопределенностей с помощью правила Лопиталя. Формулировка правила Лопиталя.
Пусть
в некоторой окрестности точки х = а
функции f(x)
и
![]() дифференцируемы (кроме, может быть самой
точки х = а) и
дифференцируемы (кроме, может быть самой
точки х = а) и
![]() .
.
Если
![]() или
или
![]() ,
так что предел
,
так что предел
![]() содержит неопределенность
содержит неопределенность
![]() или
или
![]() ,
,
и
существует предел отношения производных
этих функций
![]() (конечный или бесконечный),
(конечный или бесконечный),
то существует и предел отношения самих функций, причем выполняется равенство
![]()
![]() . (1)
. (1)
Это
правило остается справедливым, если х![]()
Правило может применятся несколько раз (если соблюдаются условия, при которых оно справедливо).
Применение правила Лопиталя можно комбинировать с другими приемами вычисления пределов.
Раскрытие неопределенностей или .
Вычислить следующие пределы, применяя правило Лопиталя.
Пример 1.
![]()
Решение.
Здесь
![]()
![]()
![]()
![]()
Поэтому
данный предел содержит неопределенность
![]() .
.
Так
как функции f(x)
и
![]() дифференцируемы в окрестности точки
х = –1, то попробуем вычислить
предел отношения их производных:
дифференцируемы в окрестности точки
х = –1, то попробуем вычислить
предел отношения их производных:
![]()
![]() =
=![]() =
=![]() =
=![]() .
.
Получилось,
что предел отношения производных
существует и равен числу
![]() .
На основании правила Лопиталя заключаем,
что предел отношения функций
.
На основании правила Лопиталя заключаем,
что предел отношения функций
![]() также существует и равен числу
также существует и равен числу
![]() .
.
Ответ:
![]() .
.
Пример 2.
![]() .
.
Решение.
![]()
![]()
![]()
![]()
![]()
![]()
Пояснение к символу “”:
после
того, как обнаружена неопределенность
![]() в пределе отношения производных, пробуем
вычислить предел отношения вторых
производных и эту попытку обозначаем
символом “”. В
результате получилась такая цепочка
записей:
в пределе отношения производных, пробуем
вычислить предел отношения вторых
производных и эту попытку обозначаем
символом “”. В
результате получилась такая цепочка
записей:
![]() .
.
В
конце концов предел отношения третьих
производных вычислился и равен числу
![]() .
Теперь в соответствии с правилом Лопиталя
заключаем, что все пределы отношений
предыдущих производных и самих функций
существует и равен
.
Теперь в соответствии с правилом Лопиталя
заключаем, что все пределы отношений
предыдущих производных и самих функций
существует и равен
![]() .
Поэтому получается обратная цепочка
записей
.
Поэтому получается обратная цепочка
записей
![]()
Таким образом, правило Лопиталя применено три раза, в результат получено значение искомого предела и этот факт отражается в записях с использованием символа “”.
При этом важно понимать, что если бы получилось так, что предел отношения оказался несуществующим, то это бы не означало, что не существуют и предыдущие пределы (то есть переходы “” в этом случае делать нельзя). Это только лишь означало бы, что данный предел не может быть вычислен по правилу Лопиталя.
Ответ:
![]() .
.
Пример 3.
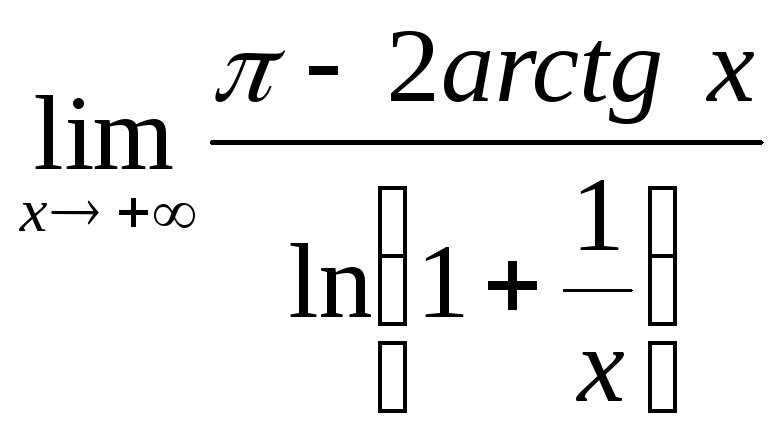 .
.
Решение.

![]()
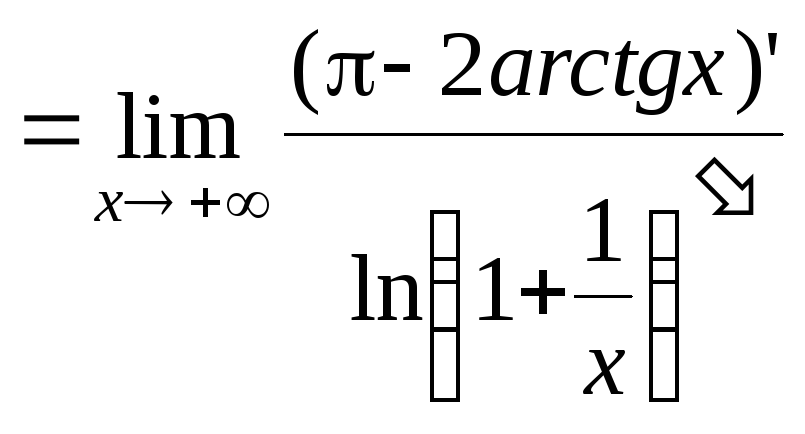 =
=
 =
=
![]()
![]()
![]()
![]()
![]() .
.
Ответ: 2.
Пример 4.
![]() .
.
Решение.
![]()
![]()
![]()
![]() =
=
![]() =
=
![]()
![]() =
=![]()
![]()
![]()
![]()
Здесь
работа по правилу Лопиталя значительно
упростилась применением теоремы о
пределе произведения, с помощью которой
была отделена функция
![]() ,
не участвующая в создании неопределенности.
,
не участвующая в создании неопределенности.
Ответ:
![]() .
.
Пример 5.
![]() .
.
Решение.
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ:
![]()
![]()
Пример 6.
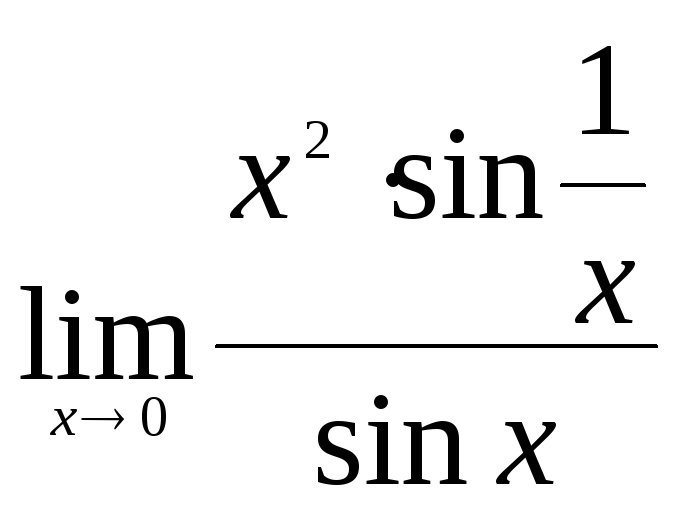 .
.
Решение.

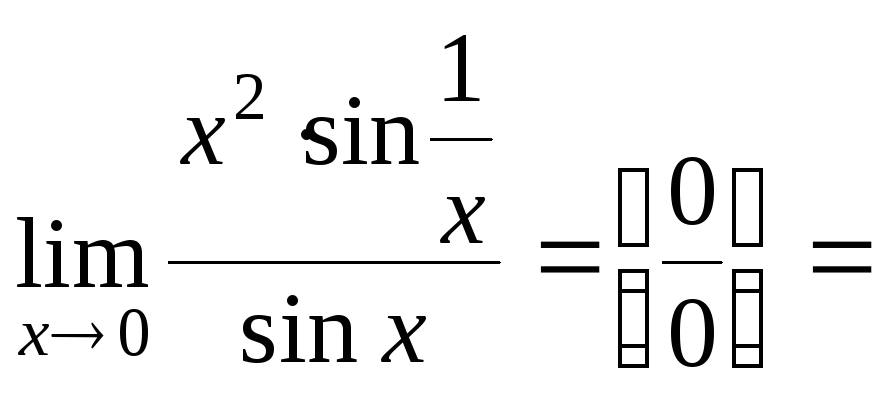


![]()
![]() – не существует.
– не существует.
Это значит, что не выполняется одно из условий правила Лопиталя – условие существования предела отношения производных двух функций. Поэтому предел отношения этих двух функций не может быть вычислен по правилу Лопиталя, хотя может существовать и быть вычислен иными приемами.
Действительно,


Таким образом, работая с пределом по правилу Лопиталя, нельзя быть уверенным в его успешном вычислении до тех пор, пока не получится значение (конечное или бесконечное) предела отношения производных некоторого порядка. Только в этом случае становятся справедливыми все равенства в цепочке
![]()
![]()
![]()
![]()
Раскрытие неопределенностей ([0], [ – ], [1], [0], 00]).
В
случае неопределенности вида [0]
или [
– ],
следует функцию, стоящую под пределом,
преобразовать алгебраически так, чтобы
привести её к неопределенности вида
![]() или
или
![]() и далее воспользоваться правилом
Лопиталя. В частности, используется
преобразование произведение к дроби:
и далее воспользоваться правилом
Лопиталя. В частности, используется
преобразование произведение к дроби:
 .
.
Неопределенности типов [1], [0], 00] раскрываются с помощью предварительного логарифмирования функции, стоящей под пределом.
Пример 7.
![]() .
.
Решение.
![]() [0]
[0]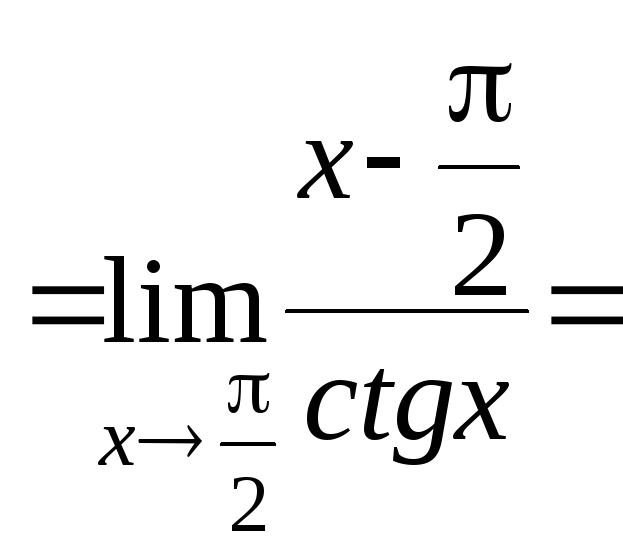
![]()
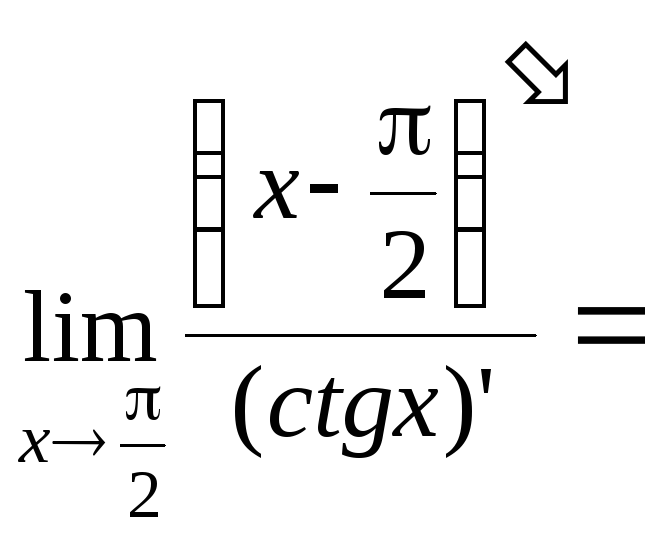
![]() .
.
Ответ:
![]() –1.
–1.
Пример 8.
![]() .
.
Решение.
![]() []
[]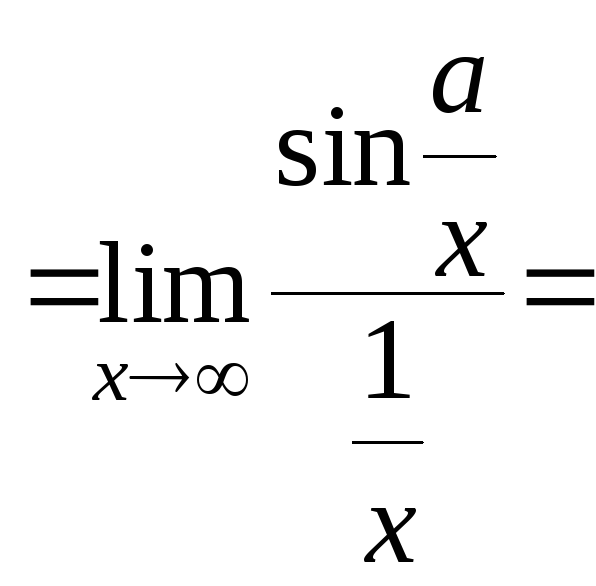
![]()

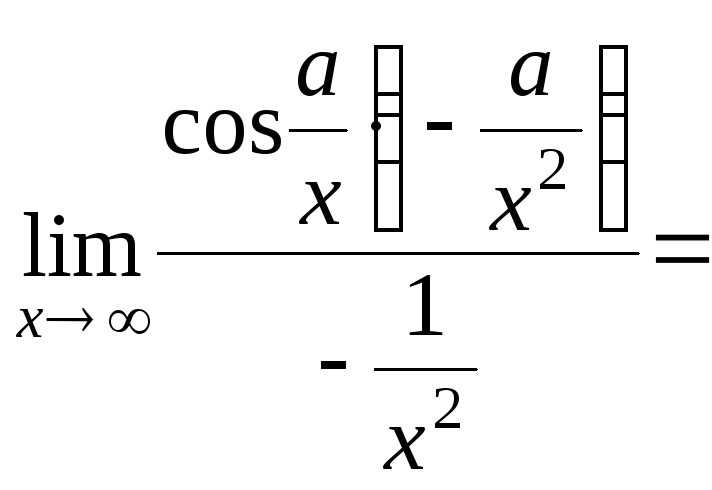
![]()
![]()
Ответ:
![]()
![]()
Пример 9.
![]() .
.
Решение.
![]() []
[]![]()
![]()
![]() =
=
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ:
![]()
![]()
Пример 10.
![]() .
.
Решение.
Данный
предел содержит неопределенность [1].
Обозначим
![]() .
Тогда
.
Тогда
![]()
Вычислим
![]()
![]()
![]()
![]() =
= ![]()

![]()
![]()
Итак,
получено, что
![]()
![]()
![]()
![]() .
.
Здесь знаки предела и логарифма были переставлены в соответствии со свойством пределов непрерывных функций:
![]() если
если
![]() непрерывная
функция в точке х = а.
непрерывная
функция в точке х = а.
Ответ:
![]() .
.
Пример 11.
![]() .
.
Решение.
Данный
предел содержит неопределенность [0].
Обозначим
![]() тогда
тогда
![]()
Вычислим
![]() [0]=
[0]=
![]()
![]()

![]() =
=![]()
Так
как
![]() то
то
![]()
Ответ:
![]()
Пример 12.
![]() =[00]
=[00]![]()
Решение.
![]()

![]()
![]()
![]() =
=![]()
![]()
![]()
![]()
![]() .
.
Получено
![]()
![]()
Здесь показана наиболее короткая запись вычислений, поясненных в предыдущих примерах.
Ответ:
![]() =1.
=1.
Дополнительные упражнения.
|
1.
|
2.
|
|
3.
|
4.
|
|
5.
|
6.
|
|
7. |
8.
|
|
9.
|
10.
|
|
11.
|
12.
|
|
13.
|
14.
|
|
15.
|
16.
|
|
17.
|
18.
|
|
19.
|
20.
|
|
21.
|
|
Ответы.
1.
![]() ; 2.
; 2.
![]() ; 3.
; 3.
![]() ; 4.
2; 5.
; 4.
2; 5.
![]() ; 6.
0;
; 6.
0;
7.
![]() ; 8.
1; 9.
; 8.
1; 9.
![]() ; 10.
–2; 11. 1; 12. 0;
; 10.
–2; 11. 1; 12. 0;
13. 0; 14.
![]() ; 15.
; 15.
![]() ; 16.
0; 17. 0; 18.
; 16.
0; 17. 0; 18.
![]() ;
;
19. 1; 20.
![]() ; 21.
1.
; 21.
1.


 ;
;