5.2 Выбор оптимальных режимных параметров

По данным таблицы 3 строим графики зависимостей выходных величин F и tкс от входных – gh, tnh и dn. Все полученные кривые являются непрерывно возрастающими. Поэтому оптимальным режимом будет базовый режим с некоторыми отклонениями.

Поиск интервала оптимальных отклонений осуществляется с помощью линеаризации статических характеристик в точке базового режима и определения коэффициентов усиления каналов из уравнения прямой.

Рисунок 1

Рисунок 2

Рисунок 3

1 – f(gh); 2 – f(tnh); 3 – f(dn);

Рисунок 4

Рисунок 5

Рисунок 6

4 – f(gh); 5 – f(tnh); 6 – f(dn);

Рисунок 3

Коэффициент усиления по каждому из шести каналов «вход-выход» определяется формулой

, где (36)

ΔY_j – приращение j-той выходной величины, %;

ΔX_i – приращение i-той входной величины, %.

По формуле (36) и данным таблицы 3, имеем

; ; ;

; ; ;

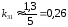Отсюда определяем каналы наибольшего влияния.

Поскольку приращение выходной переменной определяется как сумма приращений входных переменных, умноженных на соответствующие коэффициенты усиления, можно записать систему уравнений в отклонениях, добавив в неё наложенные ограничения:

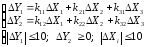; (37)

Решением этой системы является некоторая область в пространстве.

Управляя одними входами, такими как расход gh, можно компенсировать приращения выходов от влияния возмущений со стороны других входов, например, температура tnh или диаметр наружной трубы dn.

Исходя из вышесказанного, определим, насколько возможно расширить диапазоны изменений tnh и dn, используя компенсирующий канал по расходу gh:

1) ; ;

2) если неизменна dn (ΔX₃=0):

; (38)

(39)

Получаем 3 условия, накладываемые на приращение tnh:

-из уравнения (38), ;

-из уравнения (39), ;

-кроме того, должно соблюдаться условие из системы (37) .

Эти условия должны выполняться одновременно, т.к. являются ни чем иным как преобразованной системой (37). Следовательно, выбираем , или , поскольку .

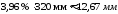3) если неизменна tnh (ΔX₂=0):

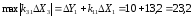; (40)

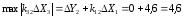. (41)

Действуя аналогично 2), находим: и .

Примечание: при определении допустимых интервалов отклонений входных переменных (в данном случае, tnh и gh), округление всегда производится в меньшую сторону, поскольку иначе отклонения выходных переменных могут превысить допустимые.

В итоге, с учётом знаков приращений, определена область оптимальных допустимых отклонений варьируемых параметров в % (рисунок 4). Варианты режимов работы аппарата при изменении одной из начальных температур потоков(tnc или tnh) даны в таблице 4.

Расчеты точек для графика:

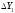1. =0

=10

10=1,32*0+1,11ΔX₂+0.26 ΔX₃

10=1.11 ΔX₂+0.36 ΔX₃

При ΔX₂=0 ΔX₃=10/0,26=38,5

При ΔX₃=0 ΔX₂=10/1,11=9,1

2. ΔX₁=0

=-10

-10=1,11 ΔX₂+0,26 ΔX₃

При ΔX₂=0 ΔX₃=-10/0,26=-38,5

При ΔX₃=0 ΔX₂=-10/1,11=-9,1

3. =10

=10

10=1,32*10+1,11 ΔX₂+0,26 ΔX₃

-3,2=1,11 ΔX₂+0,26 ΔX₃

При ΔX₂=0 ΔX₃=-3,2/0,26=-12,3

При ΔX₃=0 ΔX₂=-3,2/1,11=-2,9

4. =10

=-10

-10=1,32*10+1,11 ΔX₂+0,26 ΔX₃

-23,2=1,11 ΔX₂+0,26 ΔX₃

При ΔX₂=0 ΔX₃=-23,2/0,26=-89,2

При ΔX₃=0 ΔX₂=-23,2/1,11=-20,9

5. =-10

=-10

-10=1,32*(-10)+1,11 ΔX₂+0,26 ΔX₃

3,2=1,11 ΔX₂+0,26 ΔX₃

При ΔX₂=0 ΔX₃=3,2/0,26=12,3

При ΔX₃=0 ΔX₂=3,2/1,11=2,9

6. =-10

=10

10=1,32*(-10)+1,11 ΔX₂+0,26 ΔX₃

23,2=1,11 ΔX₂+0,26 ΔX₃

При ΔX₂=0 ΔX₃=23,2/0,26=89,2

При ΔX₃=0 ΔX₂=23,2/1,11=20,9

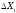=0

=0

0=1,16 ΔX₂ ΔX₂=0

=10 0=4,6+1,16 ΔX₂

ΔX₂=-4,6/1,16=-3,96

ΔX₁=-10

ΔX₂=4,6/1,16=3,96

параметры	базовый режим	варианты отклонений
		А	В	С	D
gh, т/ч	100	от 100 до 90	от 100 до 90	от 100 до 110	от 100 до 110
tnh, °С	320	320	От 320 до 332,6	320	От 320 до 319,7
dn, мм	295	От295до305	295	От295до285	295
tкс, °С	245,6	≥ 245,6
F, м2	243,7	от 219 до 268

Вариант А (C): в результате возмущений по каналу dn, значение диаметра наружной трубы увеличилось (уменьшилось) от номинального на величину от 0 до 10мм. Для компенсации этого возмущения, необходимо уменьшить (увеличить) расход gh на величину от 0 до 10 т/ч. Следовательно, возможные диапазоны изменений величин dn и gh составят соответственно 295...305 (285...295) и 90…100 (100…100). Вариант В (D) отличается от варианта А (С) тем, что возмущения поступают по каналу tnh.

Во всех вариантах, значения контролируемых параметров F и tkc могут отклоняться в допустимых пределах (±10% и ≥0%) от номинального значения, т.е. в диапазонах 219...268 м²· и ≥245,5 °С соответственно. Поскольку допустимые приращения tnh и dn рассчитаны с учетом всех наложенных условий (система (37), то работа теплообменника в пределах приведенных режимов гарантирует их выполнение.

Реакция системы управления на возмущения по каналам tnh и dn может быть определена с помощью рисунка 4. Заштрихованная область рисунка соответствует отсутствию компенсации (∆gh = 0), а затемненная область – наличию компенсации, которая расширяет пределы допустимых возмущений. Соответственно, на линиях границ затемнённой области компенсация принимает максимально возможное значение, а вне её – становится недостаточной для покрытия всех возмущений.

Точка А с координатами ∆dn = ∆tnh = 1%, лежащая в заштрихованной области, соответствует набору возмущений, при котором ∆F = 1,37% и ∆tkc = 1,16%. Эти приращения не превосходят допустимые. Следовательно, в компенсации нет необходимости.

В точке Б (∆dn=∆tnh=5%) ∆F = 6,85% и ∆tkc = 5,8%. Эти приращения не превосходят допустимые. Следовательно, в компенсации нет необходимости.

Точка В (∆dn=9, ∆tnh=3%) ∆F = 10.77% и ∆tkc = 10.44% что превышает 10%, следовательно, придется задействовать компенсирующий канал, т.е. изменить расход теплоносителя таким образом, чтобы он вызвал обратное приращение поверхности теплообмена.

В точке Г (∆dn=∆tnh= -3%) ∆F = -4,11% и ∆tkc = -3,48%., т.е. конечная температура продукта уменьшилась по сравнению с номинальной, что недопустимо. Значит, здесь также придется задействовать компенсирующий канал.