27. Что понимают под коэффициентом корреляции двух скалярных случайных величин? Сформулируйте и докажите основные свойства коэффициента корреляции.

Коэффициентом корреляции случайных величин X и Y называют число  = (X, Y), определяемое равенством (предполагается, что DX>0 и DY>0):.

Коэффициент корреляции имеет следующие свойства:

1. (X, X) = 1

2. Если случайные величины X и Y являются независимыми (и существуют DX>0 и DY>0), то (X, Y) = 0.

3. (a₁X₁+b₁, a₂X₂+b₂) = (X₁, X₂). При этом знак плюс нужно брать в том случае, когда a₁ и a₂ имеют одинаковые знаки, минус – разные.

4. –1  (X, Y)  1

5. |(X, Y)| = 1 тогда и только тогда, когда случайные величины X и Y линейно зависимы.

Доказательство следует из свойств ковариации.

28. Дайте определение ковариационной матрицы случайного вектора. Сформулируйте и докажите основные свойства ковариационной матрицы.

Матрицей ковариаций (ковариационной матрицей) случайного вектора называют матрицу , состоящую из ковариаций случайных величин X_i и X_j.

Свойства матрицы ковариаций.

1. Матрица ковариаций является симметрической.

2. Пусть m-мерный случайный вектор получен из n-мерного случайного вектора с помощью линейного преобразования B, т. е. . Тогда матрица ковариаций случайного вектора связана с матрицей ковариаций случайного вектора 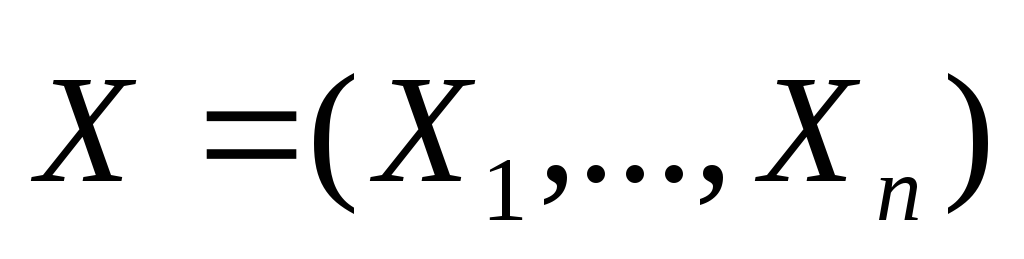соотношением .

3. Матрица ковариаций является неотрицательно определенной, т. е. для всех векторов

Доказательство. Утверждение 1 следует из определения матрицы ковариаций. Пусть матрица В линейного преобразования имеет вид B = (b_ij). Вычислим ковариацию случайных величин Y_i и Y_j: . Записывая последнее равенство в матричной форме, получаем утверждение 2. Для доказательства утверждения 3 рассмотрим скалярную случайную величину . В случае скалярной случайной величины Y ее дисперсия , и поэтому в соответствии с утверждением 2 имеем: , откуда в силу неотрицательности дисперсии получаем утверждение 3.

29. Что понимают под условным законом распределения? Докажите равенство , где - непрерывный случайный вектор.

Для двумерной дискретной случайной величины (X, Y) условной вероятностью , того, что случайная величина X примет значение x_i при условии Y = y_j, называют условную вероятность события {X=x_i} при условии события {Y=y_j}, т. е. . Набор вероятностей характеризует условное распределение дискретной случайной величины X при условии Y = y_j.

Условная функция распределения непрерывной случайной величины: .

Условная плотность распределения непрерывной случайной величины: .

Эти понятия называют условными законами распределения.

30. Дайте определение условного математического ожидания и докажите его основное свойство.

Условным математическим ожиданием M(X|Y) дискретной случайной величины X относительно дискретной случайной величины Y называют функцию M(X|Y) = g(Y) от случайной величины Y, где область определения функции g(y) совпадает с множеством значений y₁, …, y_m случайной величины Y, а каждому значению y_j аргумента y поставлено в соответствие число g(y_j) = M(X|y_j).

Свойства условного математического ожидания.

1. M(c|Y)  c

2. M(aX+b|Y) = aM(X|Y)+b

3. M(X₁+X₂|Y) = M(X₁|Y)+M(X₂|Y)

4. Пусть случайные величины X₁ и X₂ являются независимыми при условии, что случайная величина Y приняла любое конкретное значение. Тогда M(X₁X₂|Y) = M(X₁|Y) M(X₂|Y).

5. MX = M(M(X|Y))

6. Пусть u(X) и v(Y) – функции от случайных величин X и Y. Тогда M(u(X)v(Y)|Y) = v(Y) M(u(X)|Y)

7. Если X и Y – независимые случайные величины, то M(X|Y)  MX.