5

Билет №7, 11

Диэлектрические потери

4.1. ОПРЕДЕЛЕНИЯ И ОСНОВНЫЕ ПОНЯТИЯ

Диэлектрическими потерями Р (Вт) называют ту часть энергии приложенного электрического поля, которая рассеивается в диэлек­трике за единицу времени. Эта энергия переходит в тепло, и диэлек­трик нагревается.

При недопустимо высоких диэлектрических потерях электроизо­ляционная конструкция может нагреться до температуры теплового разрушения, т.е. наступит электротепловой пробой (см. гл. 5.3.1 и 5.4.2).

Диэлектрические потери электроизоляционных материалов и кон­струкций часто характеризуют тангенсом угла диэлектрических по­терь tgδ, где δ— угол, дополняющий до 90° угол сдвига фаз между то­ком и напряжением (угол φ) в емкостной цепи (рис. 4.1):

δ= 90°-φ. (4.1)

Величина tgδ является важной характеристикой диэлектриков. Она определяет диэлектрические потери в материале: чем больше tgδ, тем более высокие (при прочих равных условиях) диэлектриче­ские потери. Для наиболее широко применяемых диэлектриков tgδ имеет значение в пределах от 0,0001 до 0,03. О величине диэлектри­ческих потерь участка изоляции и некоторых радиодеталей (конден­саторов, катушек индуктивности и т.п.) можно судить также по зна­чению их добротности Q:

Q=-1/tgδ = ctgδ = tg φ. (4.2)

Диэлектрические потери могут быть как при постоянном, так и при переменном на­пряжении. При постоянном напряжении потери обусловлены только током сквозной проводимости, и величина диэлектриче­ских потерь в данном случае зависит (об­ратно пропорционально) от значений удельных объемного и поверхностного со­противлений. При переменном напряже­нии диэлектрические потери возникают под действием как тока сквозной проводи­мости, так и релаксационных видов поля­ ризации.

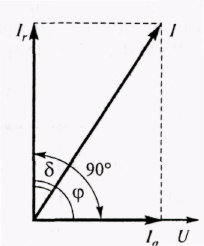
Рис 4.1. Векторная диаграмма диэлектрика с потерями.

В сильных электрических полях (в постоянном и переменном) дополнительно возникают ионизационные потери.

4.2. Эквивалентные схемы замещения диэлектрика с потерями

Чтобы изучить диэлектрические потери какого-либо материала, необходимо рассмотреть конденсатор с этим материалом в цепи пере­менного напряжения. Конденсатор с исследуемым диэлектриком, имеющий емкость С, рассеиваемую мощность Р и угол сдвига фаз ме­жду током и напряжением φ, заменим эквивалентной схемой, в кото­рой к идеальному конденсатору активное сопротивление подключено либо параллельно — параллельная эквивалентная схема, либо после­довательно — последовательная эквивалентная схема. Эти эквива­лентные схемы замещения диэлектрика с потерями должны быть вы­браны так, чтобы расходуемая в них активная мощность была равна мощности Р, которая рассеивается в конденсаторе с исследуемым ди­электриком, а ток опережал бы напряжение на тот же угол φ. Эквива­лентные схемы вводятся условно и не объясняют механизма диэлек­трических потерь. Величины емкости идеального конденсатора и активного сопротивления для параллельной и последовательной схем замещения обозначим соответственно Ср и R, Cs и r.

Параллельная эквивалентная схема замещения диэлектрика с по­терями и векторная диаграмма токов в ней представлены на рис.4.2, из которого видно, что активная составляющая тока Iа совпадает по фазе с напряжением U, а реактивная составляющая тока Ir опережает напряжение на угол, равный 90°. Значения соответствующих токов равны

I = U/Z, Ia = U/R, Ir = U/Xc = UωCp, (4.3)

где Z — полное сопротивление, Z = (Xc² + R²) ^1/2; Xс — реактивное (емко­стное) сопротивление конденсатора с диэлектриком, Xс = 1/ω Ср (ω — угловая частота).

Из треугольника токов (см. рис. 4.2, б) следует, что

tgδ = Ia/Ic = U/ RUωCp = 1/ωRCp (4.4)

Для параллельной схемы замещения, используя выражение (4.7) и векторную диаграмму токов, изображенную на рис. 4.2, б, получим

P=UIcosφ = UI sin δ = U Ir sinδ / cosδ = UIr, tgδ,

Рис. 4.2. Параллельная эквивалентная схема замещения диэлектрика с потерями (а) и векторная диаграмма токов в ней (б)

где I = Ir /cosδ (см. рис. 4.2, б).

Подставив в это выражение из (4.3) значение тока Ir получим

P = U ² ω Cp tgδ (4.8)

Для последовательной схемы замещения имеем (без вывода)

P= U² tgδ /(Xc(1+ tgδ )) P = U² ωCstgδ /(1+ tg²δ )) (4.9)

Приравняв друг к другу правые части выражений (4.8) и (4.9), (4.4) и (4.5), определим соотношения между Ср и Cs, а также между Rиr:

Cp = Cs/(1+ tg²δ )) (4-10)

R = r(1+ 1/tg²δ )) (4.11)

Для высококачественных диэлектриков значением tg²δ в сравне­нии с единицей можно пренебречь и считать, что Ср ~ Cs ~ С. Тогда величина мощности, рассеиваемой в диэлектрике, будет одинакова для обеих схем и равна

P = U²ωC tgδ (4.12)

где Р — активная мощность, Вт; U — напряжение, приложенное к конденсатору с испытуемым диэлектриком, В; С — его емкость, Ф; ω — угловая частота, с^-1 (ω = 2πf , где f - циклическая частота, Гц).

Для диэлектриков с высокими значениями tgδ при переменном напряжении емкость С и, следовательно, диэлектрическая проницае­мость ε становятся величинами неопределенными, зависящими от выбора модели эквивалентной схемы замещения. Величина же tgδ диэлектриков от выбранной схемы замещения не зависит. Она зави­сит от природы материала, частоты f напряжения и температуры Т. Поэтому в справочной литературе для каждого диэлектрика указыва­ются f и Т, при которых измерены tgδ и ε.

Из формулы (4.12) следует, что величина рассеиваемой мощности Р (диэлектрические потери) зависит от квадрата приложенного на­пряжения и его частоты, емкости и tgδ материала. Емкость, в свою очередь, зависит от ε материала, а ε и tgδ — от природы материала (химического состава и структуры) и внешних условий (температу­ры, частоты и величины напряжения, влажности среды и т.п.). Сле­довательно, все перечисленные факторы будут влиять на величину рассеиваемой мощности в диэлектриках. Из формулы (4.12) также видно, что диэлектрические потери могут приобретать существенные и даже опасные значения для диэлектриков, используемых в уста­новках высокого напряжения или высокой частоты и особенно в ус­тановках при одновременном воздействии высокого напряжения и высокой частоты.