05 семестр / К экзамену-зачёту / Ответы на экзамен 2 / Билет №18-2

1

Билет №18-2

ТЕОРИЯ МЕТАЛЛОВ ДРУДЕ

ОСНОВНЫЕ ПРЕДПОЛОЖЕНИЯ МОДЕЛИ ДРУДЕ

В 1897 г. Томсон открыл электрон. Это открытие оказало громадное и непосредственное воздействие на теорию материи и позволило также объяс­нить проводимость металлов. Через три года после открытия Томсона Друде разработал свою теорию электро- и теплопроводности. При этом он рассматри­вал электроны в металле как электронный газ и применил к нему кинетическую теорию газов, оказавшуюся весьма плодотворной.

В кинетической теории, в ее самой простой форме, считают, что молекулы газа представляют собой одинаковые твердые сферы, которые движутся по пря­мым линиям до тех пор, пока не столкнутся друг с другом¹⁾. Предполагается, что продолжительность отдельного столкновения пренебрежимо мала и что между молекулами не действует никаких иных сил, кроме возникающих в мо­мент столкновения.

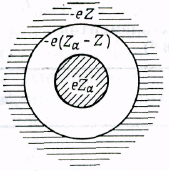
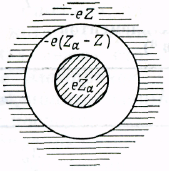
В простейших газах имеются лишь частицы одного сорта, в металлах же их должно быть по меньшей мере два: электроны заряжены отрицательно, а металл в целом электрически нейтрален. Друде предположил, что компен­сирующий положительный заряд принадлежит гораздо более тяжелым части­цам, которые он считал неподвижными. В то время, однако, еще не понимали точно, почему в металле имеются подобные легкие подвижные электроны и более тяжелые неподвижные положительно заряженные ионы. Решение этой пробле­мы стало одним из фундаментальных достижений современной квантовой теории твердого тела. При обсуждении модели Друде, однако, нам будет достаточно просто предположить (для многих металлов это предположение оправдано), что когда атомы металлического элемента объединяются, образуя металл, валентные электроны освобождаются и получают возможность свободно передвигаться по металлу, тогда как металлические ионы остаются неизменными и играют роль неподвижных положительных частиц теории Друде. Эта модель схемати­чески изображена на фиг. 1.1. Каждый отдельный атом металлического эле­мента имеет ядро с зарядом eZ_a, где Z_а — атомный номер и е — величина заряда электрона: е = 4,80•10^-10ед. СГСЭ = 1,60•10^-19 Кл. Вокруг ядра располо­жено Z_а электронов с полным зарядом — eZ_а. Некоторое число Z из них — это слабо связанные валентные электроны. Остающиеся Z_а — Z электронов доволь­но сильно связаны с ядром; они играют меньшую роль в химических реакциях и носят название электронов атомного остова. Когда изолированные атомы объединяются, образуя металл, электроны атомного остова остаются связанны­ми с ядрами, т. е. возникают металлические ионы. Валентные же электроны, наоборот, приобретают возможность далеко уходить от «родительских» атомов. В металлах эти электроны называют электронами проводимости.

К такому «газу», состоящему из электронов с массой m, которые (в отличие от молекул обычного газа) движутся на фоне тяжелых неподвижных ионов, Друде применил кинетическую теорию. Плотность электронного газа можно рассчитать следующим образом.

1) Или же со стенками сосуда, в котором они содержатся. Возможностью этого обычно пренебрегают при рассмотрении металлов, исключая случаи, когда нас интересуют эффекты в тонких проволочках, тонких пластинах или поверхностные эффекты.

Фиг. 1.1. а — схематическое изображение изолированного атома (масштабы не соблюдены); 6 — в металле ядро и ионный остов сохраняют ту же конфигурацию, что и в изолирован­ном атоме, а валентные электроны покидают атом и образуют электронный газ.

Металлический элемент содержит 0,6022•10²⁴ атомов на 1 моль (число Авогадро) и ρ/А молей на 1 см3, где ρ — массовая плотность (в граммах на 1 см3), а А — относительная атомная масса. Поскольку вклад каждого атома равен Z электронов, число электронов на 1 см³, n = N/V, есть n = 0,6022•10²⁴ (1.1)

а

_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

)

б)

В табл. 1.1 приведены плотности электронов проводимости для некоторых металлов. Обычно они имеют порядок 10²² электронов проводимости в 1 см³ и изменяются от 0,91•10²² для цезия до 24,7•10²² для бериллия. В табл. 1.1 приведены также значения величины r_s, широко применяемой как мера плот­ности электронов, r_s — радиус сферы, объем которой равен объему, приходя­щемуся на один электрон проводимости. Таким образом, V/N = 1/n = 4π r_s³ /3, r_s = ( ¾ πn) ^1/3 (1/2)

Плотность газа электронов проводимости примерно в 1000 раз больше плотности классического газа при нормальных температуре и давлении. Несмот­ря на это и несмотря на наличие сильного электрон-электронного и электрон-ионного взаимодействия в модели Друде для рассмотрения электронного газа в металлах почти без изменений применяются методы кинетической теории нейтральных разреженных газов.

Приведем основные предположения теории Друде.

1. В интервале между столкновениями не учитывается взаимодействие электрона с другими электронами и ионами. Иными словами, принимается, что в отсутствие внешних электромагнитных полей каждый электрон движется с постоянной скоростью по прямой линии. Далее, считают, что в присутствии внешних полей электрон движется в соответствии с законами Ньютона; при этом учитывают влияние только этих полей, пренебрегая сложными дополнительными полями, порождаемыми другими электронами и ионами. Приближе­ние, в котором пренебрегают электрон-электронным взаимодействием в про­межутках между столкновениями, известно под названием приближения неза­висимых электронов. Соответственно приближение, в котором пренебрегают электрон-ионным взаимодействием, называется приближением свободных электро­нов. В последующих главах мы обнаружим, что приближение независимых электронов оказывается неожиданно удачным во многих отношениях, тогда как от приближения свободных электронов приходится отказаться, даже если мы хотим достичь лишь качественного понимания поведения металлов.

Р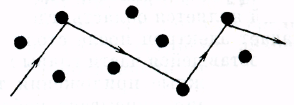ис.1.2

2. В модели Друде, как и в кине­тической теории, столкновения — это мгновенные события, внезапно меняю­щие скорость электрона. Друде связывал их с тем, что электроны отскакивают от непроницаемых сердцевин ионов (а не считал их электрон-электронными столк­новениями по аналогии с доминирующим механизмом столкновений в обычном газе).

Позднее мы увидим, что при обычных условиях рассеяние электронов на электронах действительно является одним из наименее существенных механизмов рассеяния в металле. Однако простая механическая модель (рис.1.2), согласно которой электрон отскакивает от иона к иону, весьма далека от действительности. К счастью, во многих задачах это не важно: для качественного (и даже количественного) понимания проводимости металлов достаточно просто предположить существование како­го-то механизма рассеяния, не вдаваясь в подробности относительно того, каков именно этот механизм. Используя в своем анализе лишь несколько общих свойств процесса столкновения, мы можем не связывать себя конкретной карти­ной столкновений. Эти общие характерные черты описываются следующими двумя предположениями.

3. Будем предполагать, что за единицу времени электрон испытывает столкновение (т. е. внезапное изменение скорости) с вероятностью, равной 1/τ. Имеется в виду, что для электрона вероятность испытать столкновение в течение бесконечно малого промежутка времени dt равна просто dt/τ. Вре­мя τ называют временем релаксации, или временем свободного пробега; оно играет фундаментальную роль в теории проводимости металлов. Из этот предположения следует, что электрон, выбранный наугад в настоящий момент времени, будет двигаться в среднем в течение времени τ до его следующего столкновения и уже двигался в среднем в течение времени τ с момента предыду­щего столкновения 3). В простейших приложениях модели Друде считают, что время релаксации τ не зависит от пространственного положения электрона и его скорости. Позднее мы увидим, что во многих, но не во всех задачах такое предположение оказывается удивительно хорошим.

4. Предполагается, что электроны приходят в состояние теплового равно­весия со своим окружением исключительно благодаря столкновениям. Счи­тается, что столкновения поддерживают локальное термодинамическое равно­весие чрезвычайно простым способом: скорость электрона сразу же после столкновения не связана с его скоростью до столкновения, а направлена слу­чайным образом, причем ее величина соответствует той температуре, которая превалирует в области, где происходило столкновение. Поэтому чем более горячей является область, где происходит столкновение, тем большей скоростью обладает электрон после столкновения.

В оставшейся части главы мы проиллюстрируем эти положения, рассмотрев наиболее важные приложения теории и обращая внимание на то, насколько хорошо теория описывает наблюдаемые явления.

СТАТИЧЕСКАЯ ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛА

В соответствии с законом Ома ток I через проводник пропорционален паде­нию напряжения V вдоль проводника: V = IR. Сопротивление проводника R зависит от его размеров, но не зависит от величины тока или падения напряже­ния. Модель Друде позволяет объяснить такую зависимость и оценить величину сопротивления.

Обычно зависимость R от формы проводника устраняют, вводя новую величину, характеризующую уже только сам металл, из которого сделан про­водник. Удельное сопротивление ρ определяется как коэффициент пропор­циональности между напряженностью электрического поля Е в некоторой точке металла и вызываемой им плотностью тока j: Е = ρ j. (1.3)

Плотность тока j представляет собой вектор, параллельный потоку заряда; его величина равна количеству заряда, проходящему за единицу времени через единичную площадку, перпендикулярную потоку. Поэтому, если через про­водник длиной L и площадью поперечного сечения S идет постоянный ток I, то плотность тока равна j = I/S . Так как падение напряжения на проводнике равно V = EL, из формулы (1.3) следует, что V = I ρL/S и, следовательно, R = ρL/S.

Если все n электронов в единице объема движутся с одинаковой ско­ростью v, то плотность тока параллельна v. Далее, за время dt электроны сместятся на расстояние v dt в направлении v, поэтому за это время площадь S, перпендикулярную направлению тока, пересекут n (v dt)S электронов. Так как каждый электрон несет заряд —е, полный заряд, пересекающий S за вре­мя dt, равен — nevSdt, и, следовательно, плотность тока равна j = — nеv. (1.4)

В любой точке металла электроны всегда движутся в самых различных направлениях и обладают разными тепловыми скоростями. Суммарная плот­ность тока дается выражением (1.4), где v — средняя скорость электронов,

В отсутствие электрического поля все направления движения электронов равно­вероятны и среднее значение v обращается в нуль, а соответственно суммарная плотность тока также равна нулю. В присутствии поля Е средняя скорость электронов отлична от нуля и направлена противоположно полю (так как заряд электрона отрицателен). Эту скорость можно рассчитать следующим образом. Рассмотрим какой-либо электрон в нулевой момент времени. Пусть t — время, прошедшее после его последнего столкновения. Скорость этого электро­на в нулевой момент времени будет равна его скорости v₀ непосредственно после столкновения плюс дополнительная скорость —eEt/m, которую электрон приобрел после столкновения. Так как мы предполагаем, что после столкнове­ния скорость электрона может иметь любое направление, вклад от v₀ в среднюю скорость электронов равен нулю, и поэтому она равна среднему значению величины —eEt/m. Однако среднее значение t равно времени релаксации τ. Поэтому имеем

V_cp = - eEτ/m, j = (ne² τ /m)E (1.5)

Этот результат обычно формулируют, используя характеристику, обратную удельному сопротивлению,— проводимость σ = 1/ρ: j = σE; σ = ne² τ /m)

Таким образом, мы получили линейную зависимость j от Е и нашли для проводимости σ выражение, в которое входят только известные величины и время релаксации τ. Следовательно, используя (1.6) и наблюдаемые значения удельного сопротивления, можно определить величину времени релаксации: τ = m / ρne² (1.7)

В табл. 1.2 приведены удельные сопротивления некоторых типичных метал­лов при различных температурах. Обратите внимание на его сильную темпера­турную зависимость. При комнатной температуре удельное сопротивление зависит от Т примерно линейным образом, но при достижении низких темпера­тур оно резко уменьшается. При комнатной температуре удельные сопротивле­ния обычно имеют порядок одного микроом-сантиметра (мкОм•см) Если ρ — удельное сопротивление, выраженное в мкОм•см, соотношение (1.7) для времени релаксации удобно записать в виде τ = (0,22/ρ) (rs/ao)³ • 10^-14 c (1.8)

Времена релаксации, рассчитанные по формуле (1.8) с использованием удельных сопротивлений, приведенных в табл. 1.2, даны в табл. 1.3. Мы видим, что при комнатных температурах τ оказывается порядка 10^-14—10^-15с. Чтобы понять, является ли это разумным значением, полезнее рассмотреть среднюю длину свободного пробега λ= v₀τ, где v₀ — средняя скорость электронов. Длина λ характеризует среднее расстояние, проходимое электроном между столкновениями. Во времена Друде было естественным оценивать v₀ исходя из классического закона равнораспределения энергии по степеням свободы: (l/2m)v₀² = (3/2)kT. Подставляя сюда известную массу электрона, находим, что v₀ имеет порядок 10⁷см/с при комнатной температуре и, следовательно, длина свободного пробега составляет от 1 до 10 А . Так как это расстояние сравнимо с межатомным, результат вполне согласуется с предположением Друде о том, что столкновения объясняются соударениями электрона с большими тяжелыми ионами.

классическая оценка при комнатной темпе­ратуре дает значение v₀ на порядок величины меньше действительного. Кроме того, из табл. 1.3 следует, что при наиболее низких температурах τ на порядок величины больше, чем при комнатной температуре. Поскольку v₀ в действитель­ности не зависит от температуры, то оказывается, что при низких температурах длина свободного пробега может возрасти до 1000 и более ангстрем, т. е. в тысячу раз превышать межионное расстояние. В настоя­щее время, работая при достаточно низких температурах с тщательно приго­товленными образцами, можно достичь средних длин свободного пробега по­рядка 1 см (т. е. около 10⁸ межатомных расстояний). Это явно указывает на то, что электроны не просто соударяются с ионами, как предполагал Друде.

К счастью, однако, мы можем продолжать использовать для расчетов модель Друде, хотя и не совсем точно понимаем природу столкновений. Не имея теории времени свободного пробега, важно найти такие предсказания модели Друде, которые не зависят от величины времени релаксации т. Оказывается, существует несколько подобных не зависящих от т величин, которые и сегодня

по-прежнему представляют фундаментальный интерес, поскольку во многих отношениях точное количественное рассмотрение времени релаксации остается наиболее слабым звеном в современных теориях проводимости металлов. В ре­зультате не зависящие от т величины представляют особую ценность, потому что часто они дают наиболее надежную информацию.

Кратко билет 18-2.

С позиции классической электронной теории металлы рассмат­риваются как система, состоящая из положительных ионов, обра­зующих узлы кристаллической решетки, и свободных (коллективи­зированных) электронов — электронов проводимости, заполняющих остальное пространство решетки. Если к металлическому проводнику приложить электрическое поле, то у каждого электрона проводимости, кроме хаотического (теплового) движения, возникает упорядоченное движение — дрейф (рис. 12.3, б): в металле потечет электрический ток.

j = γЕ

γ = ena = enλ/2mν

У всех металлов величину средней скорости v теплового движе­ния можно считать постоянной. Концентрация n электронов прово­димости, как и скорость v, мало зависит от природы металла. Поэто­му удельная электропроводность γ металлических проводников зависит в основном от средней длины свободного пробега электрона λ, величина которой существенно влияет на подвижность а электро­нов: чем меньше λ., тем меньше а. Величина λ в свою очередь зави­сит от степени деформации кристаллической решетки металлическо­го проводника. У идеального металлического проводника при Температуре, равной 0 К, электроны проводимости не будут сталки­ваться с узлами кристаллической решетки, поэтому длина свободно пробега электрона λ, и, следовательно, электропроводность γ Должны быть бесконечно большими, а удельное сопротивление ρ pавно нулю.

С позиции волновой механики движущиеся в металле электроны проводимости обладают не только корпускулярными свойствами, но и волновыми. Следовательно, основными их параметрами являются не только масса, скорость и энергия, но и частота, и длина волны. Движение электрона в металле с позиции волновой механи­ки — это распространение электронной волны в твердом теле, а сопротивление металла возникает в результате рассеяния электронной волны на тепловых колебаниях решетки и ее дефектах, размеры которых соизмеримы с расстоянием порядка четверти длины волны электрона.

Влияние температуры на удельное сопротивление.

Концентрация n электронов проводимости в металлических про­водниках от температуры не зависит, однако от температуры зависит их подвижность а.

ТКр=1/ρ dρ /dT.

TKρ = 1/ρ1 (ρ2-ρ1) / (T2-T1)

У сплавов, образующих твердые растворы, ТКρ имеет минимальное значение, используется для получения термически высокостабильных образцовых проволочных резисторов.

У технически чисто­го металлического проводника на небольшом участке 1, составляющем несколько Кельвинов, наблюдается «остаточное» со­противление рост, величина которого не зависит от температуры, но сильно зависит от наличия примесей. Чем чище металл, тем мень­ше рост и уже участок 1. Рост удельного сопротивления с тем­пературой на участке II объясняется тем, что при нагревании вклю­чаются все новые частоты тепловых колебаний (фононов) кристал­лической решетки, на которых рассеиваются носители заряда. При температуре, примерно равной T_θ, спектр колебаний возбуждается полностью. При дальнейшем повышении температуры (уча­сток III) удельное сопротивление растет практически прямо про­порционально увеличению температуры. На этом участке ρ возрастает, так как при нагревании прямо пропорционально увели­чиваются амплитуды тепловых колебаний узлов кристаллической решетки.