05 семестр / К экзамену-зачёту / Ответы на экзамен 2 / Билет №19-2

Билет №19-2

ТЕПЛОЕМКОСТЬ ПРИ НИЗКИХ ТЕМПЕРАТУРАХ

Чтобы провести более общее обсуждение теплоемкости, заметим прежде всего, что в пределе большого кристалла набор дискретных векторов, по кото­рому ведется суммирование в выражении (23.12), становится плотным в мас­штабе тех характерных расстояний в k-пространстве, на которых слагаемые в (23.12) испытывают существенные изменения. Поэтому мы можем заменить сумму интегралом, поступая согласно общему правилу (2.29) для произволь­ного набора волновых векторов, удовлетворяющих граничным условиям Борна — Кармана, и записать выражение (23.12) в виде

(23.15)

причем интегрировать следует по первой зоне Бриллюэна. С учетом упрощений при очень низких температурах выражение (23.15) принимает вид

где интеграл берется по всему k-пространству.

Фиг. 23.1. Упрощения, используемые для расчета низкотемпературной удельной теплоем­кости гармонического кристалла.

а — типичные кривые дисперсии нормальных мод двухатомного кристалла вдоль некоторого направления в k-пространстве (имеющего достаточно высокую симметрию, поскольку две акустические и две оптиче­ские моды вырождены).

б — спектр, заменяющий кривые, приведенные на фиг.а, при расчете интеграла (23,15). Акустические ветви заменяются прямыми, неограниченно продолжающимися в область произвольно больших значений k (т. е. интегрирование по первой зоне Бриллюэна заменяется интегрированием по всему k-пространству); оптическими ветвями при этом пренебрегают. Такие упрощения оправданы, поскольку большие по срав­нению с k_в T/ħ частоты (части дисперсионных кривых на фиг. а и б, лежащие выше горизонтальной штри­ховой линии) вносят пренебрежимо малый вклад в интеграл (23.15), а части дисперсионных кривых, отве­чающие модам, которые действительно вносят вклад в величину (23.15) (участки кривых ниже горизон­тальной штриховой линии), на фиг. а и б совпадают. Квантовая теория гармонического кристалла 85

……………….. при очень низких температурах имеем

(23.20)

Для справедливости формулы (23.20) необходимо, чтобы величина k_вT/ħ была мала по сравнению со всеми частотами фононов, не лежащими на линей­ном участке спектра; отсюда следует, что величина k_вT/ħ должна составлять малую долю характерной частоты на границах зоны. Для выполнения подоб­ного условия температура Т должна быть значительно ниже комнатной. Так как при уменьшении температуры ниже комнатной закон Дюлонга и Пти начи­нает нарушаться, существует достаточно широкая область температур, в кото­рой не применимы ни низкотемпературный, ни высокотемпературный расчеты, а следует использовать общую формулу (23.15). На практике, однако, в этой промежуточной области температур часто используют интерполяционные методы.

ТЕПЛОЕМКОСТЬ ПРИ ПРОМЕЖУТОЧНЫХ ТЕМПЕРАТУРАХ. МОДЕЛИ ДЕБАЯ И ЭЙНШТЕЙНА

В самых первых квантовых расчетах теплоемкости решетки, проведенных Эйнштейном и Дебаем, не использовался спектр фононов в его общем виде, рас­смотренном выше, а предполагалось, что закон дисперсии нормальных мод имеет некоторую особенно простую форму. Результаты этих расчетов, построен­ных на грубой аппроксимации закона дисперсии нормальных мод', исполь­зуются теперь в качестве интерполяционных формул. Кроме того, теория Дебая оказала значительное влияние на принятую терминологию и определила даже способ представления экспериментальных данных.

ИНТЕРПОЛЯЦИОННАЯ СХЕМА ДЕБАЯ

В модели Дебая все ветви колебательного спектра заменяются тремя вет­вями с одним и тем же линейным законом дисперсии 3)

ω = ck. (23.21)

Кроме того, в формуле (23.15) вместо интеграла по первой зоне Бриллюэна берется интеграл по сфере радиусом k_D , выбираемым так, чтобы эта сфера содер­жала ровно N разрешенных волновых векторов, где N — число ионов в кристалле. Поскольку объем k-пространства, приходящийся на один волновой вектор, равен (2π)³/V (см. т. 1, стр. 50), это означает, что величина (2π) ³ N/V должна равняться 4π k_D³ /3 и, следовательно, k_D определяется соотношением1)

(23.22)

После этих упрощений формула (23.15) приобретает вид

(23.23)

При вычислении интеграла в (23.23) удобно определить дебаевскую частоту

(23.24)

и дебаевскую температур

k_Bθ_D = ħω_D = ħck_D (3.25)

Легко видеть, что 1/k_D характеризует среднее расстояние между частицами в кристалле, частота ω_D имеет порядок максимальной частоты фононов, а θ_D представляет собой характерную температуру; выше нее возбуждены все моды, а ниже некоторые моды начинают «вымерзать»

2).Произведем замену переменных ħck/k_BT = х; тогда в формулу (23.23) будет входить лиш дебаевская температура:

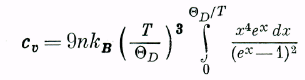
(23.26)

Эта формула выражает удельную теплоемкость при всех температурах через один эмпирический параметр θ_D. Разумный способ выбора θ_D (хотя и далеко не единственный из используемых) — потребовать, чтобы выражение (23.26) согласовывалось с наблюдаемой удельной теплоемкостью при низких тем­пературах. Это будет обеспечено (по крайней мере в гармоническом прибли­жении), если связь скорости с в формулах (23.21) или (23.25) с точным фоношшм спектром описывается формулой (23.18). Получающееся выражение для низко­температурной теплоемкости таково :

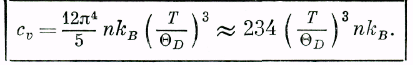(23.27)

a) Температуры Дебая определялись путем подгонки наблюдаемых удельных теплоемкостей Cv к формуле Дебая (23.26) в точке, где Cv = 3nk_B/2. Данные взяты из статьи де Лоне [3].

Таким образом

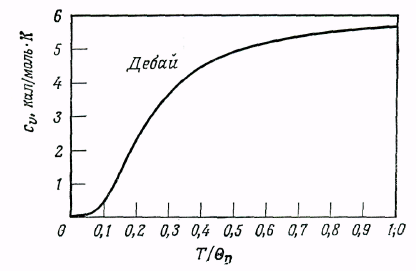
Фиг. 23.3. Зависимость удельной теплоемкости в дебаевском приближении от T/θ_D. ( из работы [3].)

дебаевская температура играет в теории колебаний решетки такую же роль, какую температура Ферми играет в теории электронов в металлах: обе они представляют собой характерные температуры, отделяющие низкотемператур­ную область, где нужно пользоваться квантовой статистикой, от высокотем­пературной области, где справедлива классическая статистическая механика. Однако в случае электронов реальные температуры всегда гораздо ниже Т_F ,. тогда как дебаевская температура θ_D (см. табл. 23.3) обычно порядка 10² К поэтому нам могут встретиться как квантовый, так и классический режимы.

Краткое объяснение температуры Дебая.

ДЕБАЯ ТЕОРИЯ твёрдого тела — теория, описываю­щая колебания кристаллич. решётки и обусловленные ими термодинамич. свойства твёрдого тела; предложена П. Дебаем в 1912 в связи с задачей о теплоёмкости кристалла. Д. т. основана на упрощённом представ­лении твёрдого тела как изотропной упругой среды, атомы к-рой совершают колебания в конечном диапазо­не частот.

Кристаллич. решётка, состоящая из N элемен­тарных ячеек по v атомов в каждой, имеет 3Nv—6 ≈ 3Nv колебат. степеней свободы. С механич. точки зре­ния, такую систему можно описывать как совокупность 3Nv независимых осцилляторов, каждый из к-рых со-

ДЕБЯ ЗАКОН ТЕПЛОЁМКОСТИ — теоретически выведенная П. Дебаем в 1912 ф-ла, согласно к-рой теп­лоёмкость С твёрдого тела при низких темп-pax Т пропорц. кубу темп-ры:

C = 2/5 π² kV (kT/ ћ c) ³ ( 1 )

где V — объём, с — ср. скорость звука. При низких темп-pax можно не делать различия между теплоём­костью при пост, объёме Cv и пост, давлении Ср, по­скольку в данному случае Ср

Для всех твёрдых тел при T~0 теплоёмкость решёт­ки удовлетворительно описывается ф-лой ( 1 ). Это связано с тем, что при низких темп-pax дебаевское приближение (см. Дебая теория) соответствует харак­теру колебат. спектра твёрдого тела: существованию трёх акустич. ветвей колебаний Различие проявляется вблизи температурных границ Тгр применимости теории Дебая. Для простых кристаллич. решёток (элементы и простые соединения) порядка неск. десятков К. Для более сложных решёток, а также для анизотропных струк­тур (например, квазидвумерных и квазиодномерных) существенно ниже

При сравнении эксперим. результатов с Д. з. т. имеется в виду только теплоёмкость решётки и исключается её электронная и др. составляющие (см. Тепло­ёмкость).

Лит. см. при ст. Дебая теория.

ДЕБАЯ ТЕМПЕРАТУРА — характеристич. темп-ра твёрдого тела, вводимая соотношением:

kT_θ = ћω_D ( 2 )

где ω_D — макс, частота колебаний кристаллич. ре­шётки, определяемая из условий равенства числа ко­лебаний, приходящихся на частотный интервал от 0 до ω_D, полному числу колебат. степеней свободы решёт­ки (см. Дебая теория).