1. Теоретические положения по решению задачи.

1.1. Определение конуса

Возьмем прямоугольный треугольник A'S'O' и будем вращать его вокруг катета S'O' (рисунок 3а). Любая точка гипотенузы A'S' опишет окружность, плоскость которой перпендикулярна к катету S'O'. Вся гипотенуза опишет кривую поверхность, которая называется конической поверхностью. Второй катет О'А' опишет часть плоскости в форме круга.

Таким образом, конус представляет собой геометрическое тело, ограниченное боковой конической поверхностью и плоскостью ос­нования, пересекающей все его образующие.

Прямая S'O' — ось конуса, точка S' — его вершина, a S'A' — об­разующая конуса. Перпендикуляр, опущенный из вершины конуса на плоскость его основания, называется высотой. Конусы разделяют на прямые (рисунок 3 а, в) и наклонные (рисунок 3б). Прямым круговым называется конус, у которого основанием служит круг, а высота про­ходит через центр основания. На рисунке 3в изображен усеченный конус, который можно рассматривать как геометрическое тело, образо­ванное вращением прямоугольной трапеции вокруг боковой стороны С'О', перпендикулярной к основанию.

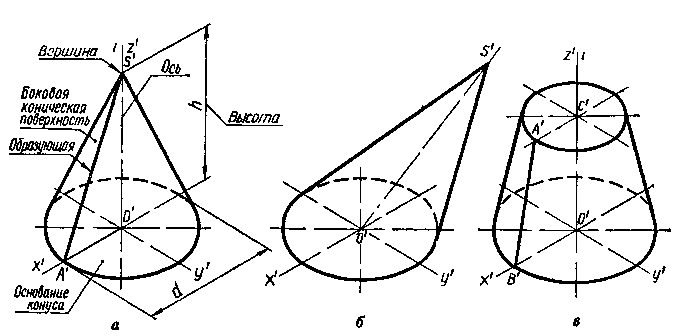
Рисунок 3.

1.2. Сечения конуса плоскостью

В зависимости от направления секущей плоскости в сечении конуса могут быть получены следующие фигуры:

а) окружность, если секущая плоскость параллельна основанию конуса (рисунок 4а);

б) треугольник, если плоскость проходит через вершину конуса (рисунок 4б);

в) полный или усеченный эллипс, если секущая плоскость наклоне на к оси под углом, большим угла наклона образующей к оси (рисунок 4в). Усеченный эллипс получается тогда, когда плоскость пересекает основание конуса;

г) парабола, если секущая плоскость параллельна образующей конуса, т. е. наклонена к оси конуса под углом, равным углу наклона образующей к оси, и не проходит через вершину (рисунок 4г);

д) гипербола, если секущая плоскость параллельна двум образую­щим конуса (т. е. если плоскость наклонена к оси под углом, меньшим, чем угол наклона образующей к оси) и не проходит через вершину или параллельна оси (рисунок 4д).

Рисунок 4.

1.3. Развертка конуса

Если разрезать поверхность конуса вдоль его образующей и развернуть эту поверхность на плоскость, то получится развертка боковой поверхности в виде кругового сектора (рисунок 5). Его радиус равен длине образующей l, а длина дуги сектора - длине окружности основания. Угол α при вершине S может быть вычислен по формуле .

2. Содержание, объем и порядок выполнения задания.

2.1. Задача №1: Построить проекции прямого кругового конуса и проекции линии сечения его фронтально-проецирующей плоскостью.

Построим проекции прямого кругового конуса, стоящего основанием на горизонтальной плоскости. Высота конуса Н = 100 мм, радиус основания конуса r = 40 мм. По индивидуальному варианту определить положение фронтального следа секущей плоскости по данным координатам z₁, z₂ точек 1, 2 (Рисунок 6).

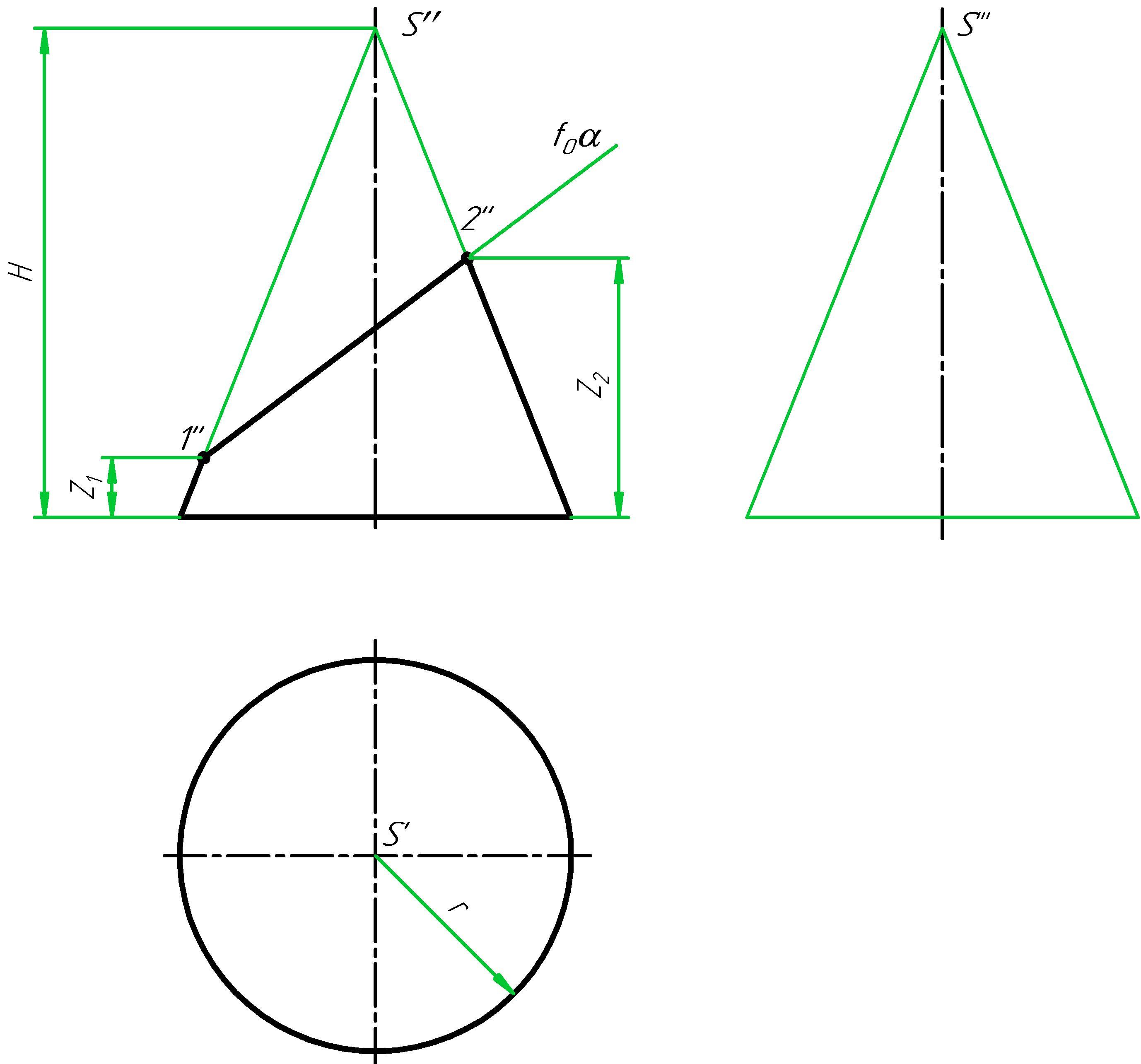
Рисунок 6

В сечении конуса данной плоскостью получается полный эллипс, так как секущая плоскость пересекает все образующие конуса и наклонена к его оси под углом большим, чем угол наклона образующих. Эллипс имеет большую ось (1-2) и меньшую ось (3-4). Оси в эллипсе взаимно перпендикулярны и проходят через середину друг друга. На фронтальной проекции эллипс, а значит его большая ось (1-2) и меньшая ось (3-4) совпадают со следом секущей плоскости, так как фронтально-проецирующая плоскость является плоскостью частного положения (перпендикулярна фронтальной плоскости проекций П₂) и поэтому обладает собирательными свойствами: собирает на свой фронтальный след проекции прямых и точек лежащих в этой плоскости.

Большая ось эллипса (1-2) в системе плоскостей П₁, П₂, П₃ занимает частное положение: она параллельна плоскости П₂. На горизонтальной и профильной проекции конуса большую ось эллипса находим по принадлежности точек 1 и 2 соответствующим образующим конуса по линиям проекционной связи (рисунок 7).

М

Рисунок 7 – Построение осей эллипса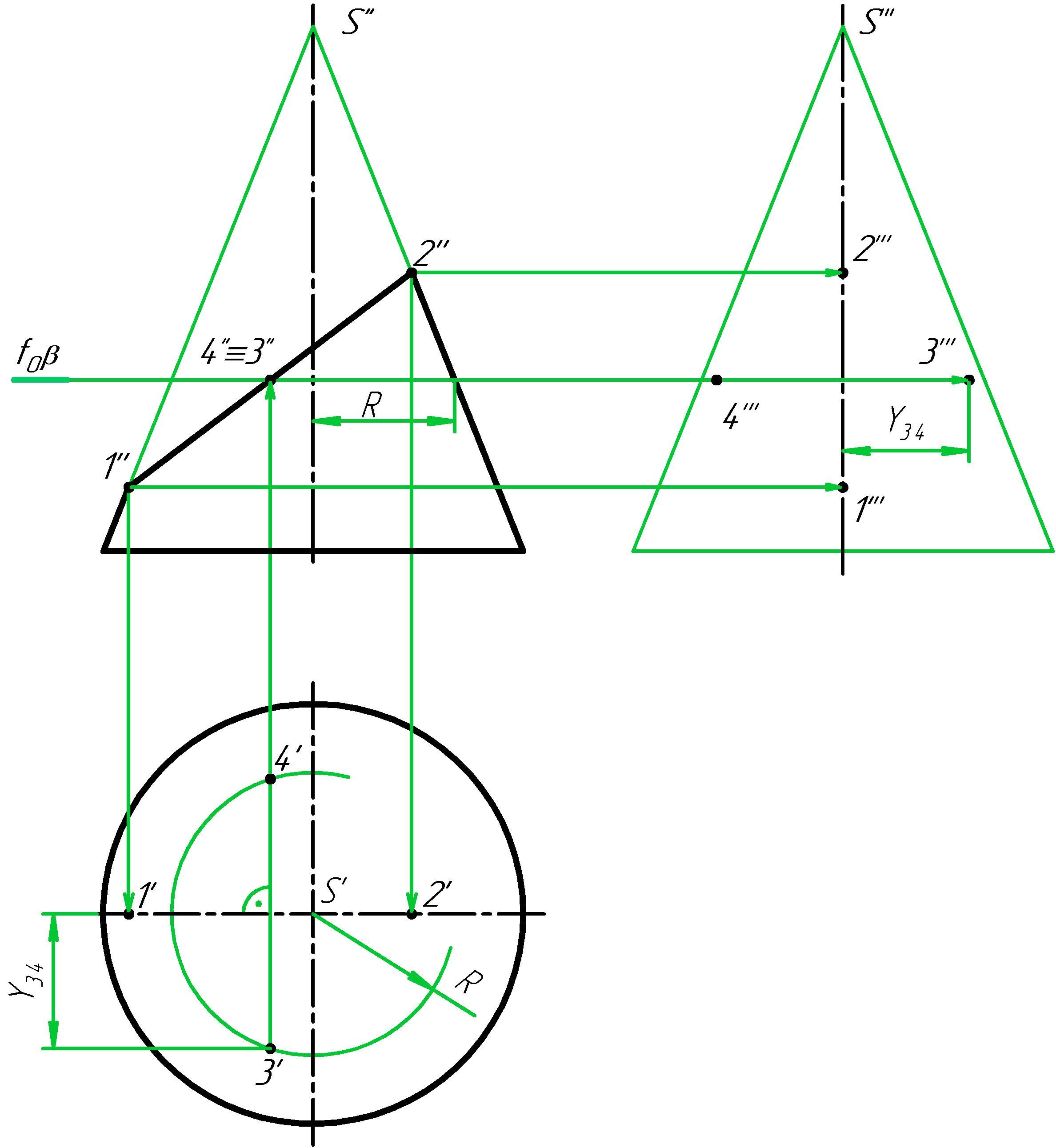

еньшая ось эллипса (3-4) занимает тоже частное положение: она перпендикулярна плоскости П₂, поэтому на фронтальной проекции конуса она проецируется в точку, которая делит большую ось (1-2) пополам, так как оси в эллипсе взаимно перпендикулярны и проходят через середину друг друга. Чтобы получить горизонтальную проекцию меньшей оси эллипса (3-4) через середину отрезка 1' - 2' надо провести перпендикуляр, а через точки 3"- 4" фронтальной проекции меньшей оси эллипса - вспомогательную горизонтальную плоскость (на рисунке 7 показан ее фронтальный след f_0), которая рассечет конус по окружности радиусом R. Строим на горизонтальной проекции окружность радиусом R, на пересечении этой окружности и перпендикуляра получим точки 3' - 4' меньшей оси эллипса, лежащие во вспомогательной горизонтальной плоскости. Профильные проекции точек 3 – 4 находим по линиям проекционной связи (рисунок 7).

К

Рисунок 8

роме точек 1 – 2 , 3 – 4, которые определяют большую и меньшую оси эллипса определяются точки 5 и 6, которые являются границей видимости на профильной проекции. Точки 5 и 6 определяются по фронтальной проекции конуса при пересечении оси конуса и фронтального следа секущей плоскости (рисунок 8). Затем находим профильные проекции точек 5, 6 на внешних образующих конуса по линиям проекционной связи. Горизонтальные проекции определяем по фронтальным и профильным проекциям, откладывая координаты Y точек 5,6, отмеренные на профильной проекции (см. рисунок 8).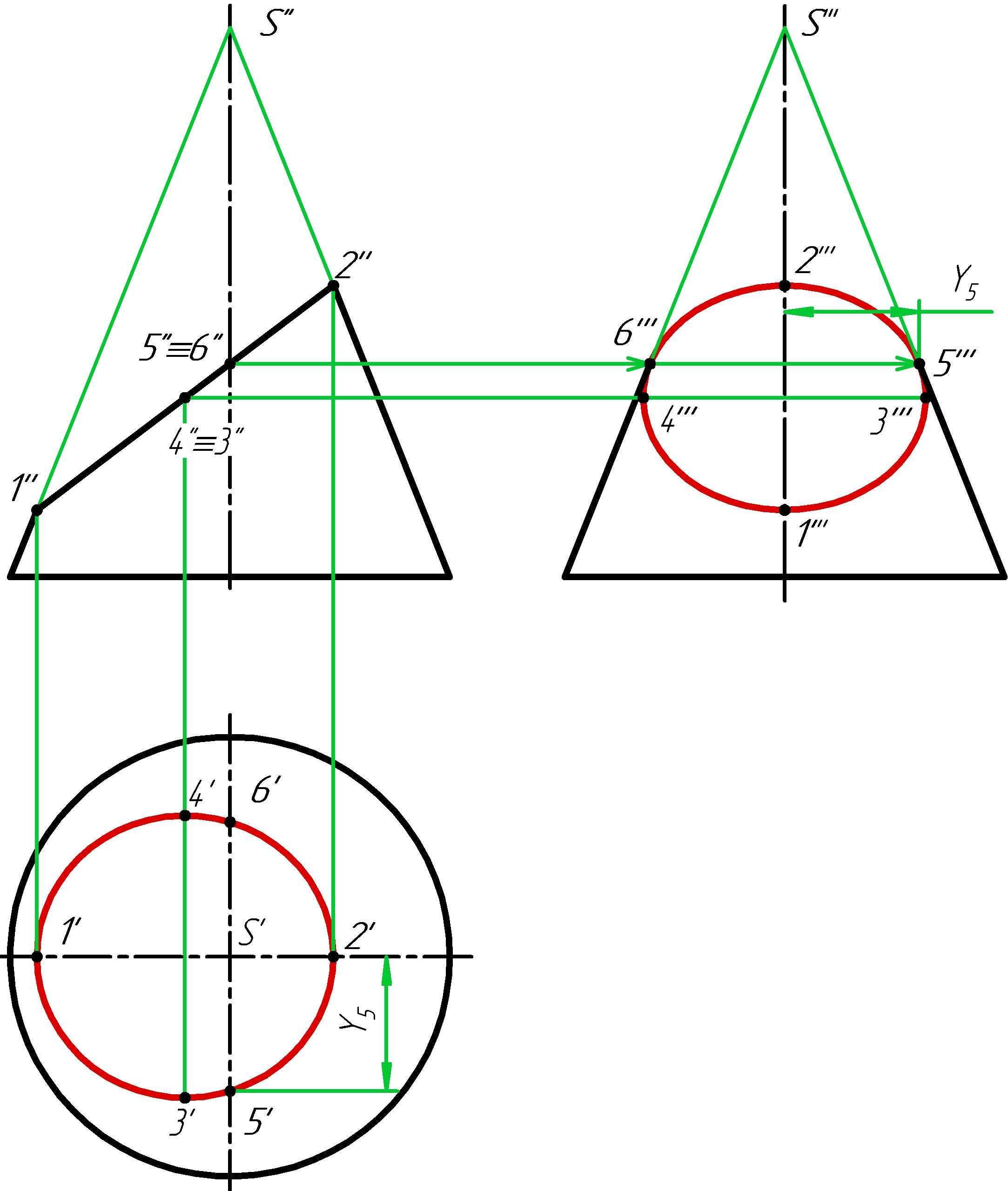

Получив точки 1, 2, 3, 4, 5, 6 соединяем их на горизонтальной и профильной проекции под лекало. Полученные проекции эллипса обводим линией красного цвета толщиной S (рисунок 8).