
- •Часть V. Распространение радиоволн в природных условиях.
- •§5.1. Влияние “плоской” земли на распространение радиоволн.
- •§5.2. Распространении радиоволн над сферической землей.
- •§5.3. Распространение радиоволн в тропосфере.
- •§5.4.Рассеяние радиоволн неоднородностями турбулентной тропосферы.
- •§5.5. Ослабление радиоволн в тропосфере.
- •§5.6. Распространение радиоволн в ионосфере.
- •§5.7. Влияние магнитного поля Земли на распространение радиоволн в ионосфере.
§5.6. Распространение радиоволн в ионосфере.
В определенных частотных диапазонах ионосфера создает благоприятные условия для распространения радиоволн вокруг Земли на весьма большие расстояния. Теория распространения радиоволн в ионосфере была развита впервые в 1923 г. М.В.Шулейкиным.
Ионосфера
представляет собой квазинейтральный
ионизированный газ, содержащий нейтральные
атомы и молекулы, положительные и
отрицательные (электроны) ионы, суммарный
заряд которых равен нулю. При этом
приятно считать, что плотность газа
такова, что среднее расстояние между
частицами
![]() .
В этом случае ионизированный газ можно
рассматривать как сплошную среду с
абсолютной диэлектрической проницаемостью
.
В этом случае ионизированный газ можно
рассматривать как сплошную среду с
абсолютной диэлектрической проницаемостью
![]() и проводимостью σ. Токами, образованными
положительными ионами, можно пренебречь
по сравнению с токами электронов,
поскольку положительные ионы обладают
значительной массой. Полная плотность
тока в ионосфере равна:
и проводимостью σ. Токами, образованными
положительными ионами, можно пренебречь
по сравнению с токами электронов,
поскольку положительные ионы обладают
значительной массой. Полная плотность
тока в ионосфере равна:
![]() ; (5.26)
; (5.26)
![]() ; (5.27)
; (5.27)
![]() ,
,
где N
– число носителей заряда в единице
объема (![]() );
);
![]() – скорость упорядоченного движения
электронов (м/с);
– скорость упорядоченного движения
электронов (м/с);
е
– заряд электрона, равный – ![]() Кл.
Кл.
Если ионосферу представить в виде сплошной среды, то под воздействием падающего поля в ней будет возникать ток с плотностью
![]() , (5.28)
, (5.28)
или
![]() ,
,
где
![]() – вектор электрической индукции.
– вектор электрической индукции.
В силу эквивалентности электромагнитных процессов в реальном ионосферном газе и воображаемой сплошной среде можно положить
![]() ,
,
![]() .
.
Для определения
скорости
![]() воспользуемся уравнением движения
электрона в поле
воспользуемся уравнением движения
электрона в поле
![]() :
:
![]() , (5.29)
, (5.29)
где
– число соударений электронов с частицами
за единицу времени;
![]() – масса электрона;
– масса электрона;
![]() – изменение количества движения
электрона за единицу времени.
– изменение количества движения
электрона за единицу времени.
Полагая
![]() ,
после подстановки в уравнение движения
(5.29)
находим:
,
после подстановки в уравнение движения
(5.29)
находим:
![]() . (5.30)
. (5.30)
С учетом (5.26), (5.28), (5.30) представим второе уравнение Максвелла в виде
![]()
откуда
![]() ;
; ![]() . (5.31)
. (5.31)
В диапазоне
радиоволн
![]() ,
поэтому можно принять
,
поэтому можно принять
![]() ;
; ![]() . (5.32)
. (5.32)
Величина
![]() имеет размерность квадрата частоты.
Эта частота, обозначаемая
имеет размерность квадрата частоты.
Эта частота, обозначаемая
![]() ,
называется плазменной частотой (или
частотой Ленгмюра):
,
называется плазменной частотой (или
частотой Ленгмюра):
![]() ,
где N
– число электронов в кубическом метре.
,
где N
– число электронов в кубическом метре.
Относительная диэлектрическая проницаемость ионосферы меньше диэлектрической проницаемости вакуума
![]() . (5.33)
. (5.33)
Из выражения для ε следует два важных вывода:
-
Эффективная электрическая проницаемость существенно зависит от , т.е. ионосфера является сильно диспергирующей средой.
-
Поскольку концентрация электронов N, а следовательно ε и σ, меняются от точки к точке, ионосферу следует считать существенно неоднородной средой.
Отметим принципиальное
отличие между изменениями диэлектрической
проницаемости в ионосфере и тропосфере.
В тропосфере она изменяется в незначительных
пределах, оставаясь несколько большей
единицы. В ионосфере диэлектрическая
проницаемость в зависимости от изменения
концентрации электронов с высотой может
принимать какие угодно значения, меньше
единицы, в том числе отрицательные. В
частности, если ε принимает нулевые или
близкие к нулю значения, то наблюдается
явление полного внутреннего отражения
радиоволн. Графики изменения N
и ε от h
для вертикального направленного луча
показаны на
рис. 5.10, а и б,
а траектории лучей при наклонном падении
- на
рис. 5.10,в
(![]() – высота, где наблюдается максимум
ионизации).
– высота, где наблюдается максимум
ионизации).
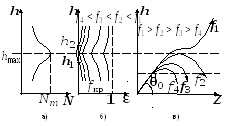
Рис. 5.10. Графики изменения N и ε от h для вертикального направленного луча.
На практике
используются понятия о критической и
максимальной частотах луча. Критической
частотой называется максимальная
частота вертикально направленного
луча, который еще отражается от
ионизированного слоя. Максимальной
частотой называется максимальная
частота луча, направленного под углом
![]() к земле, который еще отражается от слоя.
к земле, который еще отражается от слоя.
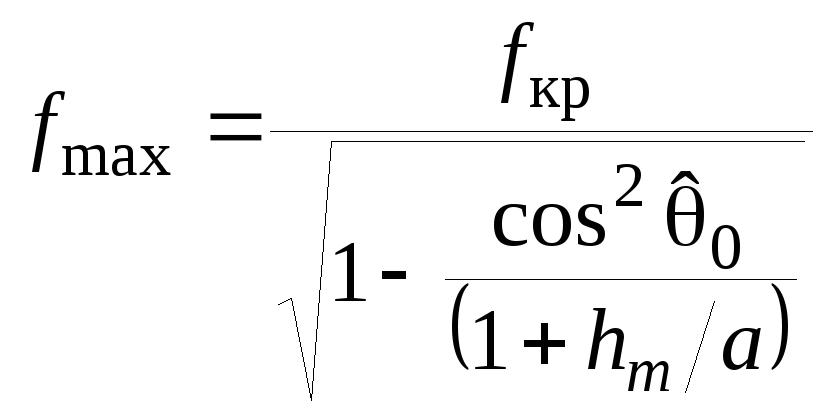 , (5.34)
, (5.34)
где a – радиус Земли.
Исследования
показывают, что максимальное значение
критической частоты не превосходит
16 МГц (λ = 19 м). Наибольшая максимальная
частота (![]() )
достигает величины 48 МГц
(λ = 6 м).
Таким образом, можно считать, что волны
короче 6 м от ионосферы не отражаются;
волны от 6 до 19 м также могут пройти
через ионосферу, не отражаясь, но при
больших углах возвышения (
)
достигает величины 48 МГц
(λ = 6 м).
Таким образом, можно считать, что волны
короче 6 м от ионосферы не отражаются;
волны от 6 до 19 м также могут пройти
через ионосферу, не отражаясь, но при
больших углах возвышения (![]() );
волны длиннее 19 м всегда отражаются
от ионосферы при любом угле возвышения.
);
волны длиннее 19 м всегда отражаются
от ионосферы при любом угле возвышения.
