
- •Механическое напряжение.
- •Перечень начал термодинамики
- •29.Работа в термодинамике. Физический смысл молярной газовой постоянной.
- •30. Теплообмен. Виды теплообмена.
- •[Виды теплообмена
- •31. Количество теплоты как мера изменения внутренней энергии при теплообмене. Удельная теплоемкость
- •32. Первое начало термодинамики. Применение первого начала термодинамики к изопроцессам. Адиабатный процесс.
- •Формулировка
- •33.Необратимость тепловых процессов. Второе начало термодинамики. Обратимые и необратимые процессы. Необратимость тепловых процессов. Второй закон термодинамики
- •34.Принцып действия тепловой машины. Кпд теплового двигателя. Цикл Карно.
- •35. Виды тепловых двигателей. Роль тепловых двигателей в научно-техническом прогрессе и охрана окружающей среды.
32. Первое начало термодинамики. Применение первого начала термодинамики к изопроцессам. Адиабатный процесс.
Первое начало термодинамики — один из трёх основных законов термодинамики, представляет собой закон сохранения энергии для термодинамических систем.
Первое начало термодинамики было сформулировано в середине XIX века в результате работ немецкого учёного Ю. Р. Майера, английского физика Дж. П. Джоуля и немецкого физика Г. Гельмгольца. Согласно первому началу термодинамики, термодинамическая система может совершать работу только за счёт своей внутренней энергии или каких-либо внешних источников энергии. Первое начало термодинамики часто формулируют как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника.
Формулировка
Существует несколько эквивалентных формулировок первого начала термодинамики
В любой изолированной системе запас энергии остаётся постоянным. Это — формулировка Дж. П. Джоуля (1842 г.).
Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил
Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе, то есть, оно зависит только от начального и конечного состояния системы и не зависит от способа, которым осуществляется этот переход. Это определение особенно важно для химической термодинамики (ввиду сложности рассматриваемых процессов). Иными словами, внутренняя энергия является функцией состояния. В циклическом процессе внутренняя энергия не изменяется.
Изменение полной энергии системы в квазистатическом процессе равно количеству теплоты Q, сообщённому системе, в сумме с изменением энергии, связанной с количеством вещества N при химическом потенциале μ, и работы A', совершённой над системой внешними силами и полями, за вычетом работы A, совершённой самой системой против внешних сил
Разделение работы на две части, одна из которых описывает работу, совершённую над системой, а вторая — работу, совершённую самой системой, подчёркивает, что эти работы могут быть совершены силами разной природы вследствие разных источников сил.
Применения первого начала термодинамики к изопроцессам.
|
|
|
|
|
|
Адиабатический процесс — термодинамический процесс в макроскопической системе, при котором система не получает и не отдаёт тепловой энергии. Серьёзное исследование адиабатических процессов началось с XVIII века.
Адиабатический процесс является частным случаем политропного процесса. Адиабатические процессы обратимы, если их проводить достаточно медленно (квазистатически). В общем случае адиабатический процесс необратим.Некоторые авторы (в частности, Л. Д. Ландау) называли адиабатическими только квазистатические адиабатические процессы.
Адиабатический
процесс для идеального
газа описывается
уравнением Пуассона.![]() Линия,
изображающая адиабатный процесс на
какой-либо термодинамической диаграмме,
называется адиабатой. Существует ряд
явлений природы, которые могут считаться
адиабатическим процессом, кроме того,
он получил применение в технике.
Линия,
изображающая адиабатный процесс на
какой-либо термодинамической диаграмме,
называется адиабатой. Существует ряд
явлений природы, которые могут считаться
адиабатическим процессом, кроме того,
он получил применение в технике.![]()
Для адиабатического процесса первое начало термодинамики в силу отсутствия теплообмена (ΔQ = 0) системы со средой имеет вид

где:
-
 —
изменение внутренней
энергии тела,
—
изменение внутренней
энергии тела, -
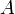 — работа,
совершаемая системой
— работа,
совершаемая системой -
 —
теплота,
полученная системой
—
теплота,
полученная системой
Основное уравнение термодинамики применительно к адиабатическому процессу записывается в дифференциалах как
![]() ,
,
где ![]() —
дифференциальное выражение для
работы, ai —
внешние параметры, Ai —
соответствующие им внутренние параметры.
—
дифференциальное выражение для
работы, ai —
внешние параметры, Ai —
соответствующие им внутренние параметры.
Энтропия системы в обратимом адиабатическом процессе не меняется[6]:
![]() .
.

